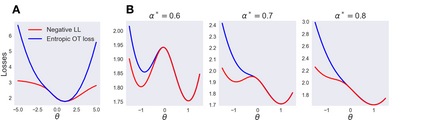
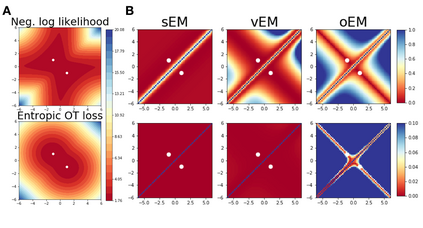
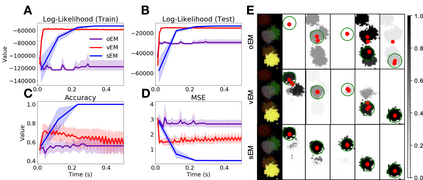
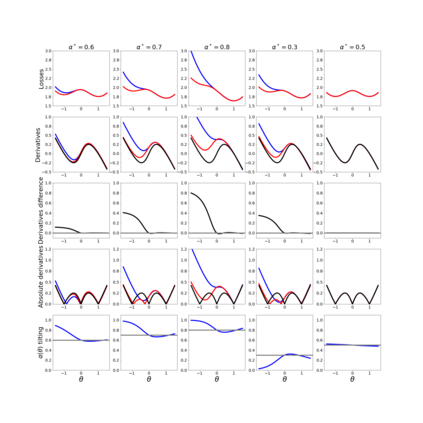
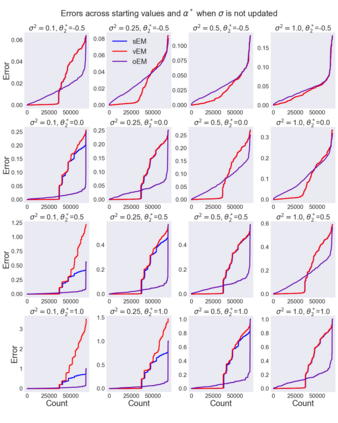
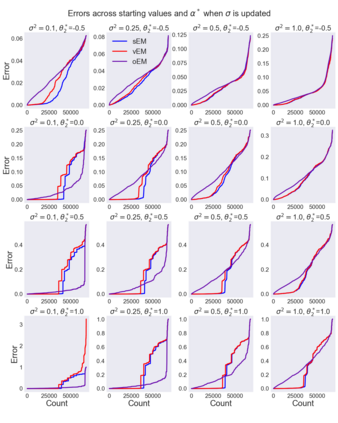
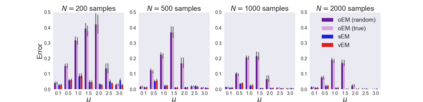
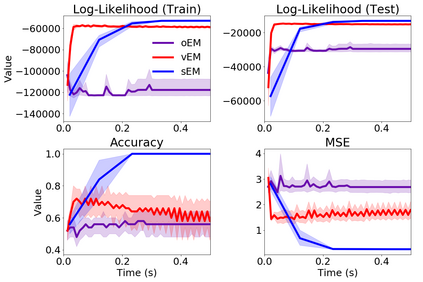
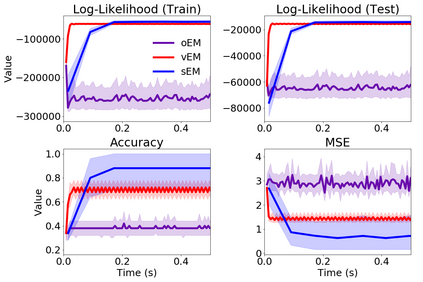
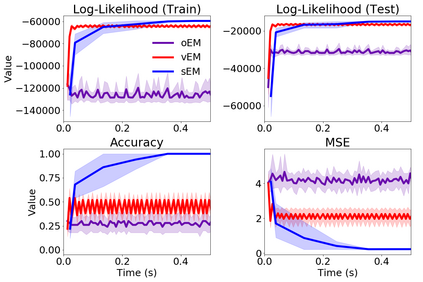
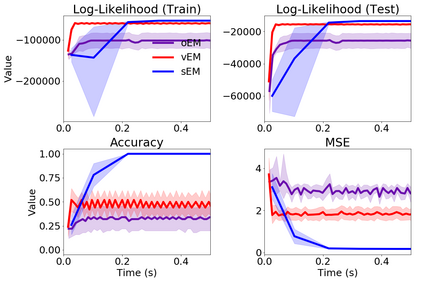
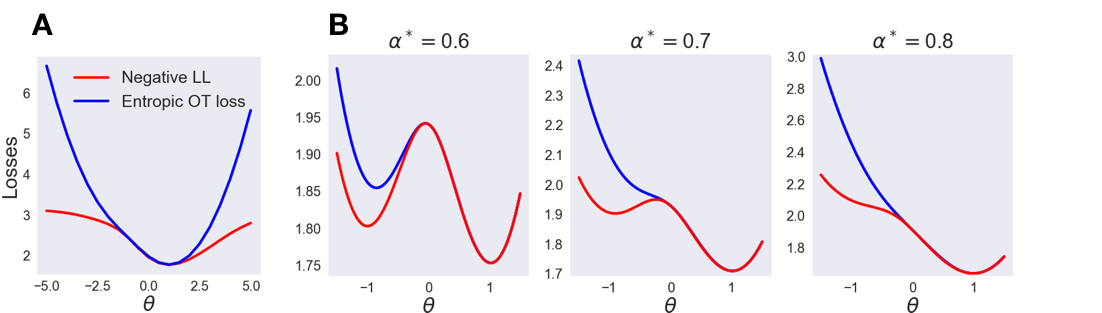
We study Sinkhorn EM (sEM), a variant of the expectation maximization (EM) algorithm for mixtures based on entropic optimal transport. sEM differs from the classic EM algorithm in the way responsibilities are computed during the expectation step: rather than assign data points to clusters independently, sEM uses optimal transport to compute responsibilities by incorporating prior information about mixing weights. Like EM, sEM has a natural interpretation as a coordinate ascent procedure, which iteratively constructs and optimizes a lower bound on the log-likelihood. However, we show theoretically and empirically that sEM has better behavior than EM: it possesses better global convergence guarantees and is less prone to getting stuck in bad local optima. We complement these findings with experiments on simulated data as well as in an inference task involving C. elegans neurons and show that sEM learns cell labels significantly better than other approaches.
翻译:我们研究Sinkhorn EM (sEM), 这是一种基于优化载运的混合物预期最大化算法的变体。 SEM 与典型的EM 算法在预期步骤期间计算责任的方式不同: SEM 使用最佳运输方式计算责任,而不是将数据点独立分配给集群,而是使用最佳运输方式来计算责任,方法是纳入关于混合重量的先前信息。像 EM 一样, SEM 具有一种自然解释作为协调升降程序,它反复构建并优化对日志相似值的较低约束。 然而,我们从理论上和经验上表明, SEM 行为优于 EM: 它拥有更好的全球趋同保证, 并且不易被困在差的本地选图中。 我们用模拟数据的实验以及涉及C. elegans 神经元的推断任务来补充这些结果, 并表明SEM 学习细胞标签比其他方法要好得多。