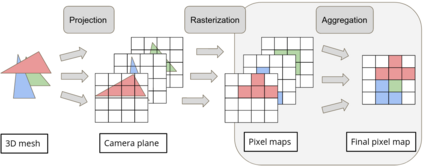
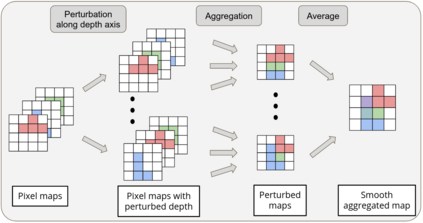
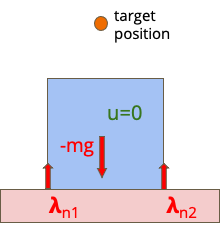
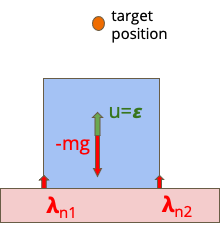
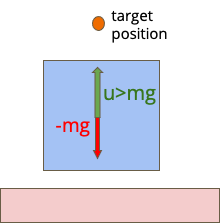
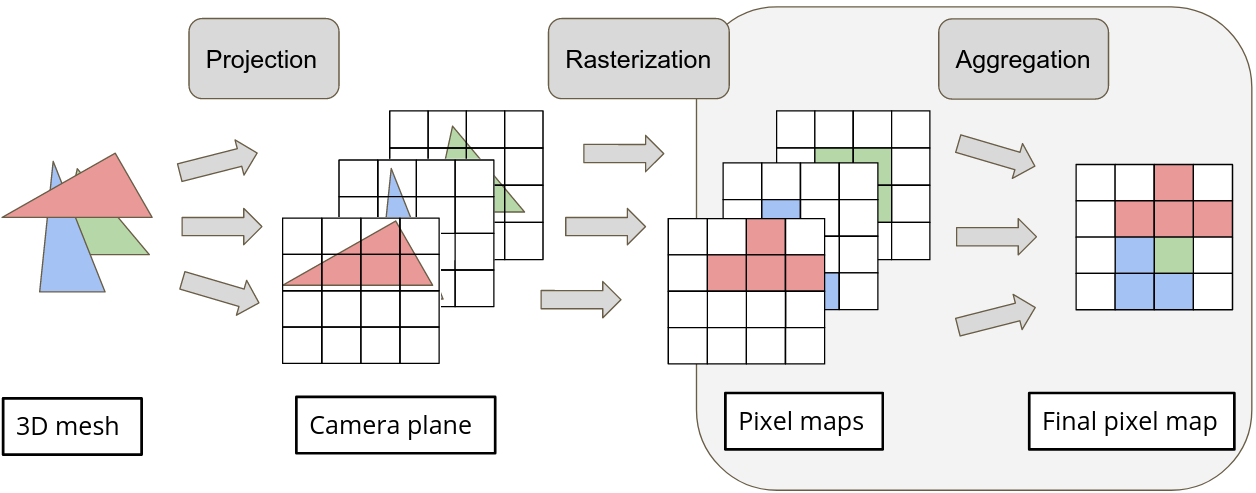
In the past few years, following the differentiable programming paradigm, there has been a growing interest in computing the gradient information of physical processes (e.g., physical simulation, image rendering). However, such processes may be non-differentiable or yield uninformative gradients (i.d., null almost everywhere). When faced with the former pitfalls, gradients estimated via analytical expression or numerical techniques such as automatic differentiation and finite differences, make classical optimization schemes converge towards poor quality solutions. Thus, relying only on the local information provided by these gradients is often not sufficient to solve advanced optimization problems involving such physical processes, notably when they are subject to non-smoothness and non-convexity issues.In this work, inspired by the field of zero-th order optimization, we leverage randomized smoothing to augment differentiable physics by estimating gradients in a neighborhood. Our experiments suggest that integrating this approach inside optimization algorithms may be fruitful for tasks as varied as mesh reconstruction from images or optimal control of robotic systems subject to contact and friction issues.
翻译:在过去几年里,根据不同的方案拟订模式,人们越来越有兴趣计算物理过程的梯度信息(例如物理模拟、图像生成等),然而,这些过程可能是无差别的,或产生不提供信息的梯度(即几乎无处不在)。在面对以前的陷阱时,通过分析表达法或数字技术(例如自动区分和有限差异)估计的梯度,使传统优化办法趋于质量差的解决方案。因此,仅仅依靠这些梯度提供的当地信息往往不足以解决涉及这些物理过程的先进优化问题,特别是当它们受到非移动和不协调问题的影响时。 在这项工作中,在零序优化领域启发下,我们随机调整平滑,通过估计附近地区的梯度来增加不同的物理学。我们的实验表明,将这一方法纳入优化算法,对于从图像中重新组合或对接触和摩擦问题的机器人系统进行最佳控制等不同的任务,可能富有成果。