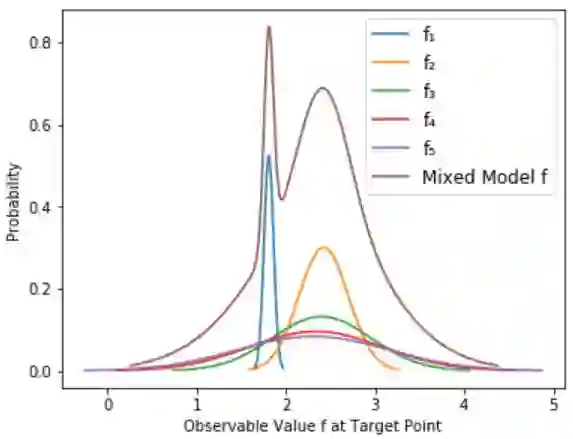
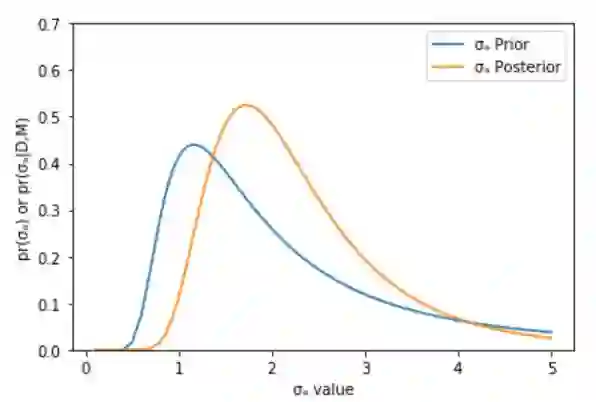
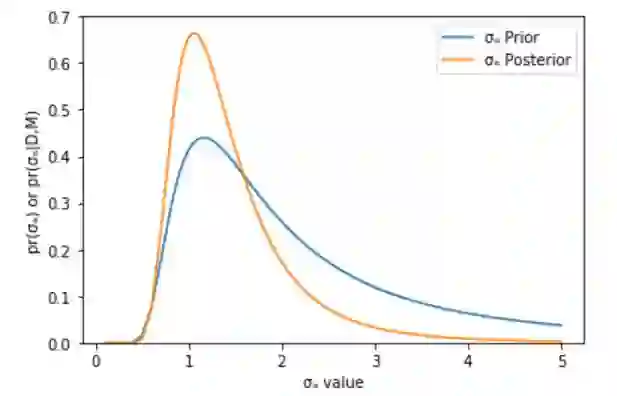
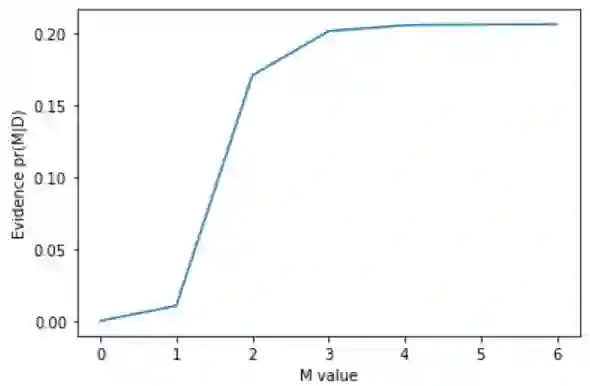
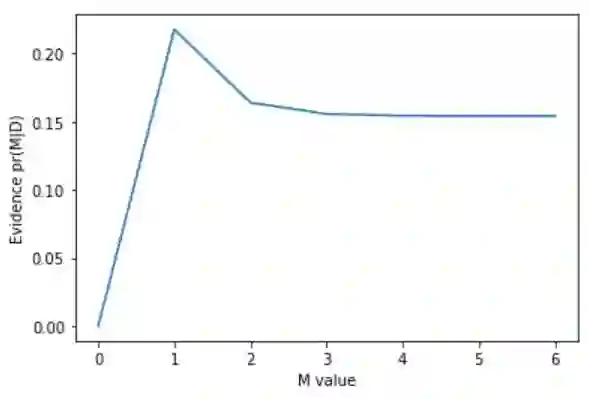
We assess the accuracy of Bayesian polynomial extrapolations from small parameter values, x, to large values of x. We consider a set of polynomials of fixed order, intended as a proxy for a fixed-order effective field theory (EFT) description of data. We employ Bayesian Model Averaging (BMA) to combine results from different order polynomials (EFT orders). Our study considers two "toy problems" where the underlying function used to generate data sets is known. We use Bayesian parameter estimation to extract the polynomial coefficients that describe these data at low x. A "naturalness" prior is imposed on the coefficients, so that they are O(1). We Bayesian-Model-Average different polynomial degrees by weighting each according to its Bayesian evidence and compare the predictive performance of this Bayesian Model Average with that of the individual polynomials. The credibility intervals on the BMA forecast have the stated coverage properties more consistently than does the highest evidence polynomial, though BMA does not necessarily outperform every polynomial.
翻译:我们从小参数值x到大数值x的Bayesian多元外推法的准确性。 我们考虑一套固定顺序的多元系数,意在作为固定顺序有效实地理论(EFT)对数据描述的替代物。 我们采用Bayesian模型动画法(BMA),将不同顺序多数值(EFT 命令)的结果合并起来。 我们的研究考虑了两个“玩具问题”,因为人们知道用于生成数据集的基本功能。 我们使用Bayesian参数估计来提取以低x表示这些数据的多元系数。 先前对系数强制规定“自然性”,因此它们是O(1)。 We Bayesian-Model-Average 不同的多数值,根据Bayesian证据加权,比较Bayesian模型平均的预测性能和单个多数值的预测性能。 BMA 预报的可信度间隔比最高证据多数值要一致,尽管BMA 不一定超越每个多元数值。