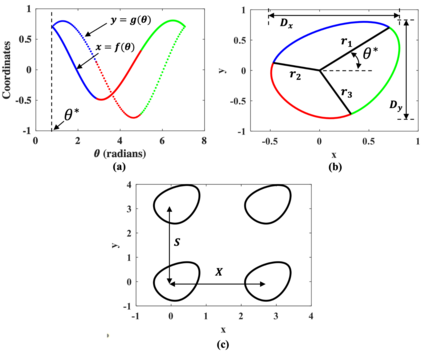
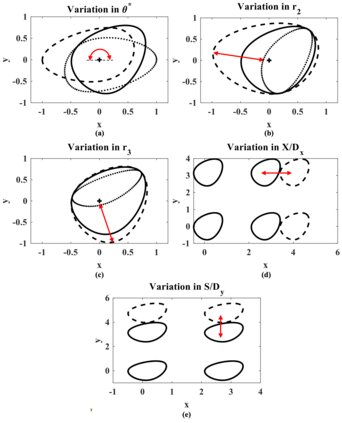
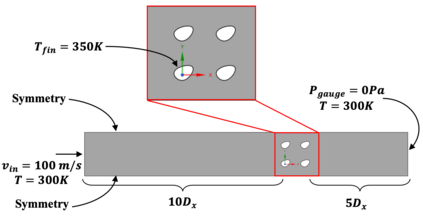
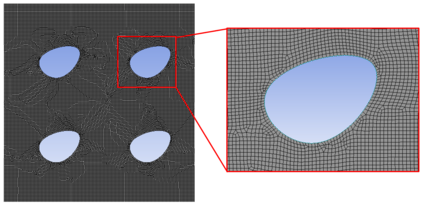
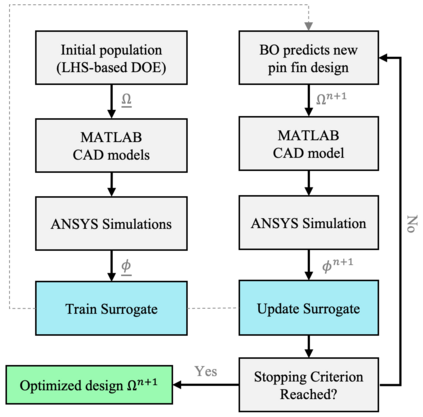
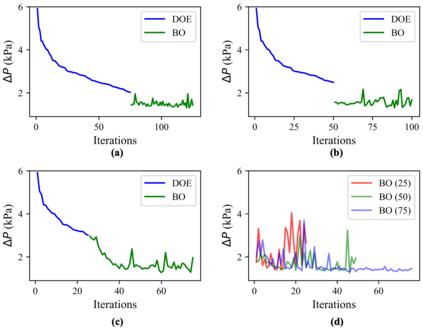
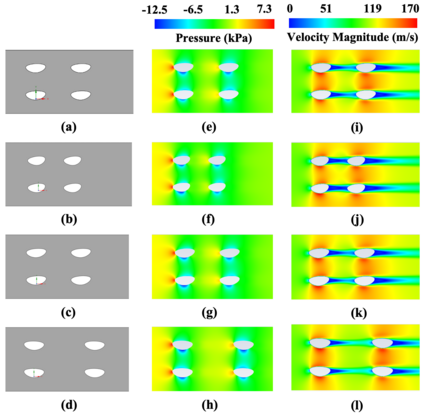
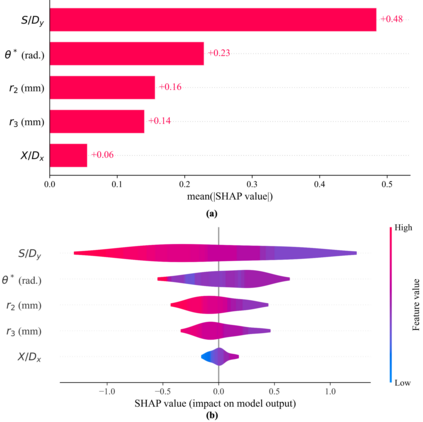
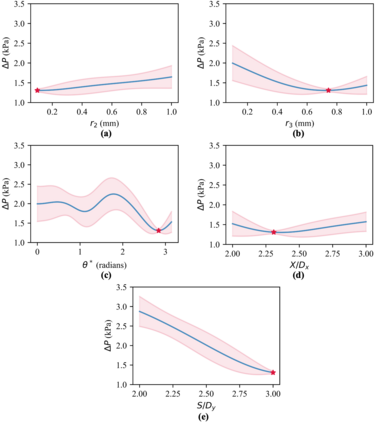
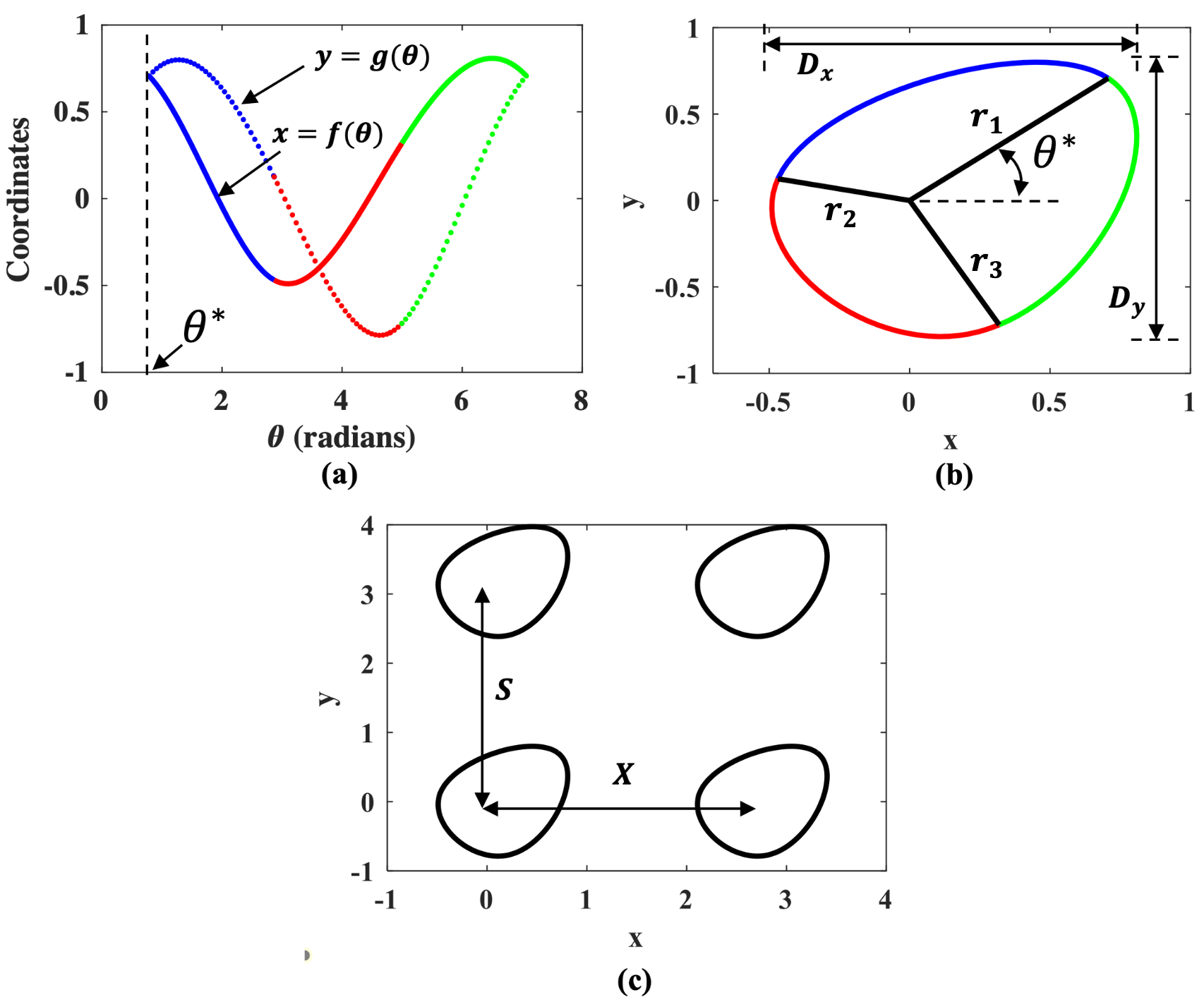
Pin fins are imperative in the cooling of turbine blades. The designs of pin fins, therefore, have seen significant research in the past. With the developments in metal additive manufacturing, novel design approaches toward complex geometries are now feasible. To that end, this article presents a Bayesian optimization approach for designing inline pins that can achieve low pressure loss. The pin-fin shape is defined using featurized (parametrized) piecewise cubic splines in 2D. The complexity of the shape is dependent on the number of splines used for the analysis. From a method development perspective, the study is performed using three splines. Owing to this piece-wise modeling, a unique pin fin design is defined using five features. After specifying the design, a computational fluid dynamics-based model is developed that computes the pressure drop during the flow. Bayesian optimization is carried out on a Gaussian processes-based surrogate to obtain an optimal combination of pin-fin features to minimize the pressure drop. The results show that the optimization tends to approach an aerodynamic design leading to low pressure drop corroborating with the existing knowledge. Furthermore, multiple iterations of optimizations are conducted with varying degree of input data. The results reveal that a convergence to similar optimal design is achieved with a minimum of just twenty five initial design-of-experiments data points for the surrogate. Sensitivity analysis shows that the distance between the rows of the pin fins is the most dominant feature influencing the pressure drop. In summary, the newly developed automated framework demonstrates remarkable capabilities in designing pin fins with superior performance characteristics.
翻译:涡轮机叶片冷却时必须佩因鳍。 因此, 针鳍的设计在过去经历了大量研究。 随着金属添加剂制造的发展, 新的设计方法现在可以用于复杂的地貌。 为此, 文章为设计内线钉提供了贝叶斯优化方法, 能够降低压力损失。 Pin- fin 形状在 2D 中使用Faturizized( parmetried) pief subline 来定义。 形状的复杂性取决于用于分析的螺丝条数量。 从方法开发的角度看, 研究使用三个螺纹线进行。 由于这个以片为根据的模型, 一种独特的针针形设计方法现在可以使用五个特性来定义。 在指定设计设计设计后, 一个计算性流期间压力下降的计算性液体动态模型。 贝因基于高斯进程而设计的顶尖形模型可以取得最佳组合, 以尽量减少压力下降。 研究结果显示, 最优化的温度设计到最短的直径直径, 最短的直径特性将显示其最短的直径直到最短的距离设计性, 最接近于现有数据最接近于最接近最精确的精确的深度, 最精确的精确的深度分析。 最接近于现有数据最接近于现有最精确的精确的精确的精确的状态。