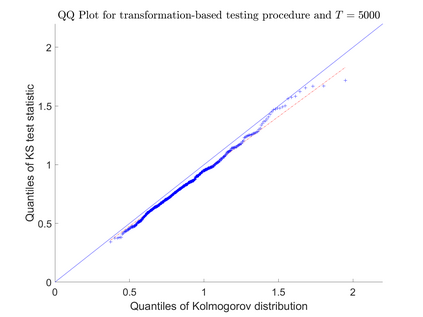
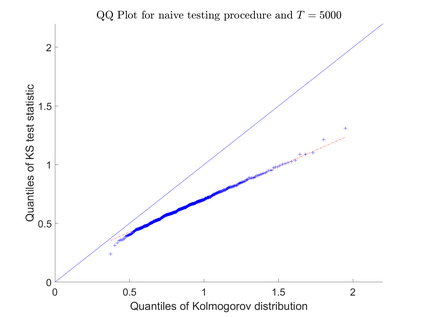
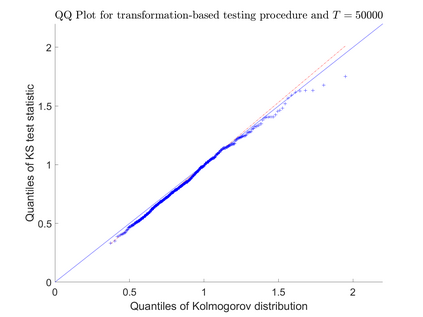
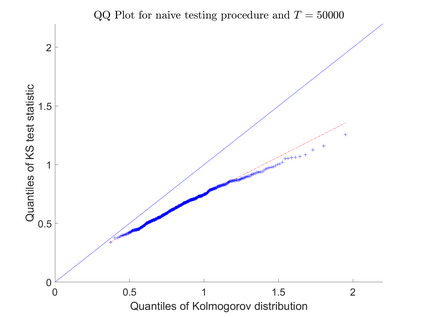
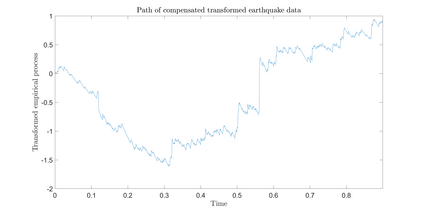
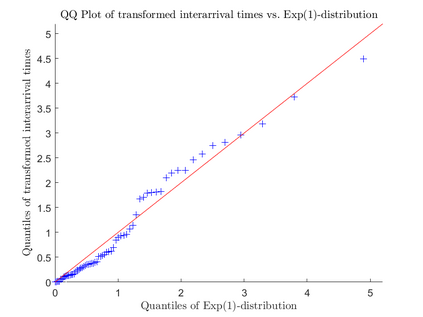
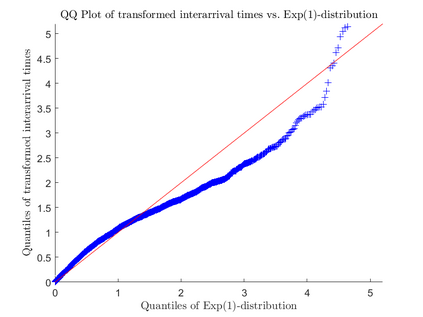
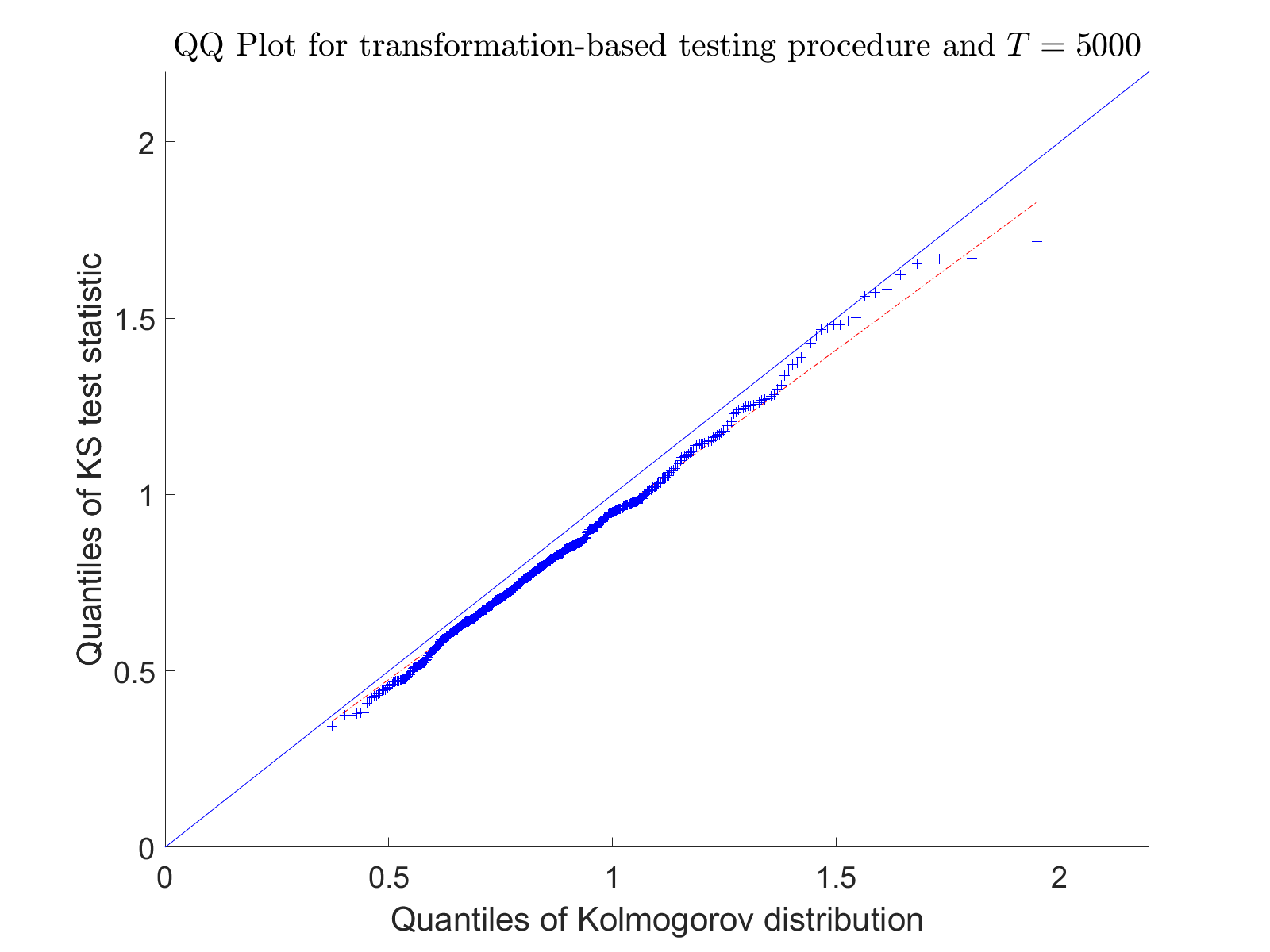
Consider an observation of a multivariate temporal point process $N$ with law $\mathcal P$ on the time interval $[0,T]$. To test the null hypothesis that $\mathcal P$ belongs to a given parametric family, we construct a convergent compensated counting process to which we apply an innovation martingale transformation. We prove that the resulting process converges weakly to a standard Wiener process. Consequently, taking a suitable functional of this process yields an asymptotically distribution-free goodness-of-fit test for point processes. For several standard tests based on the increments of this transformed process, we establish consistency under alternative hypotheses. Finally, we assess the performance of the proposed testing procedure through a Monte Carlo simulation study and illustrate its practical utility with two real-data examples.
翻译:暂无翻译