Nodal auxiliary space preconditioning for the surface de Rham complex

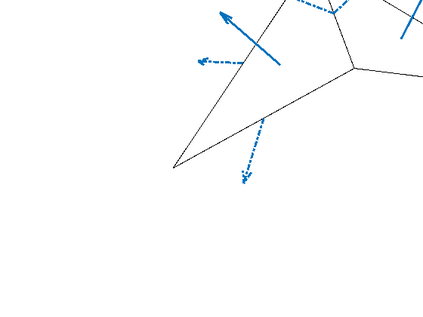
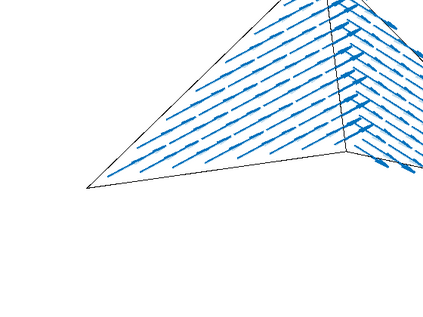
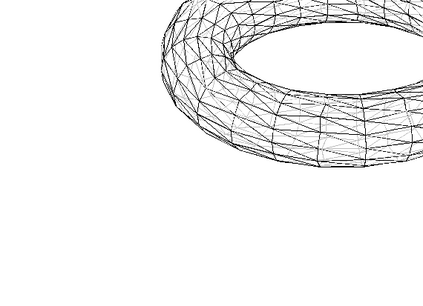
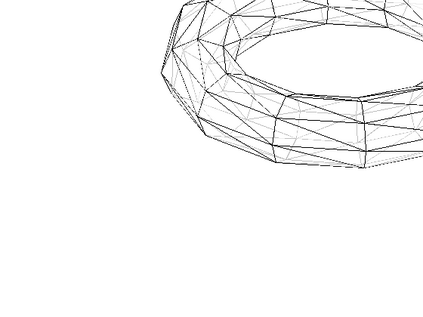
This work develops optimal preconditioners for the discrete H(curl) and H(div) problems on two and three-dimensional hypersurfaces by nodal auxiliary space preconditioning [R. Hiptmair, J. Xu: SIAM J. Numer. Anal. 45, 2483-2509 (2007)]. In particular, on unstructured triangulated surfaces, we develop fast and user-friendly preconditioners for the edge and face element discretizations of curl-curl and grad-div problems based on inverting several discrete surface Laplacians. The proposed preconditioners lead to efficient iterative methods for computing harmonic tangential vector fields on discrete surfaces. Numerical experiments on hypersurfaces are presented to test the performance of those surface preconditioners.