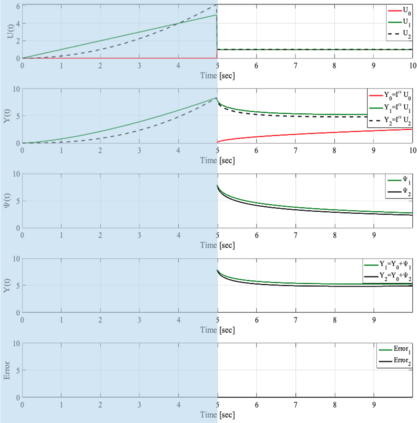
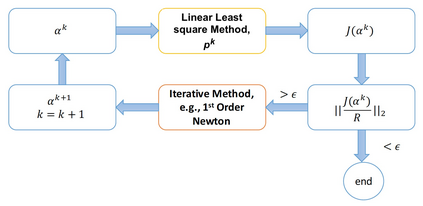
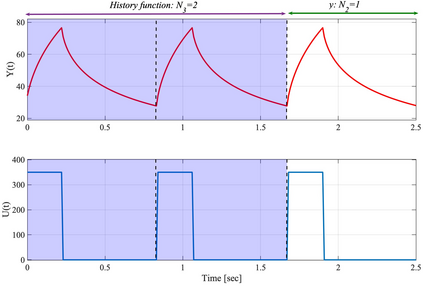
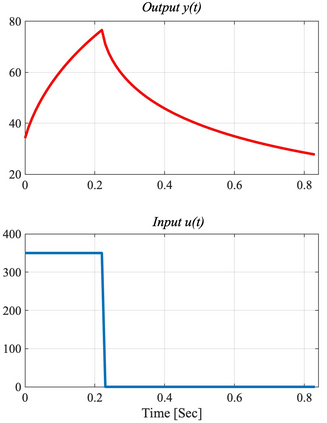
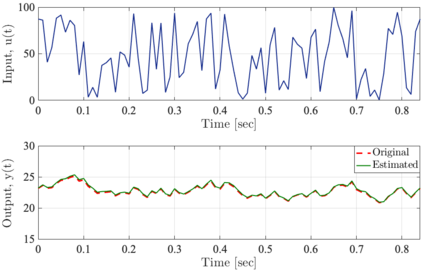
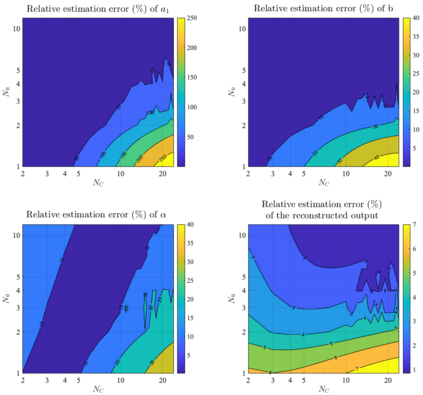
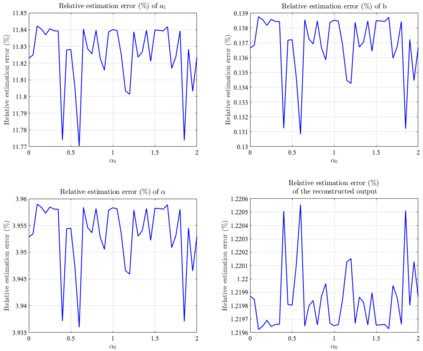
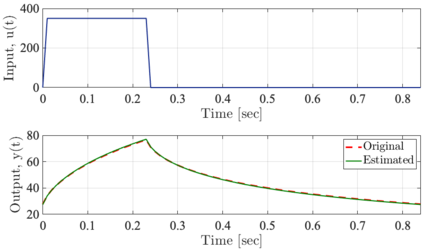
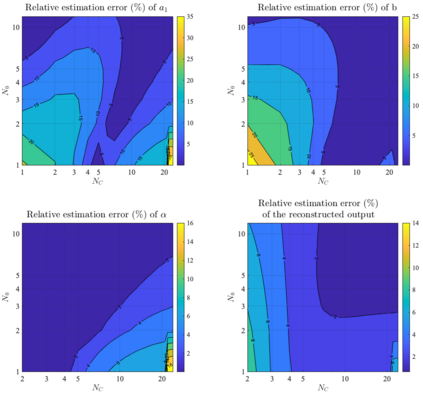
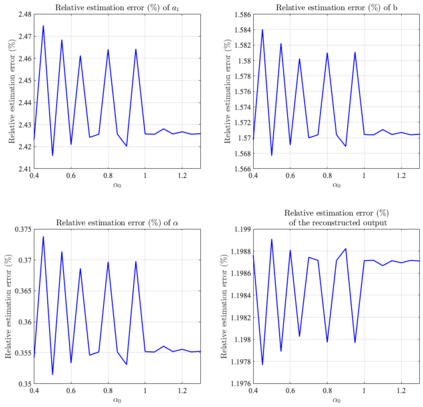
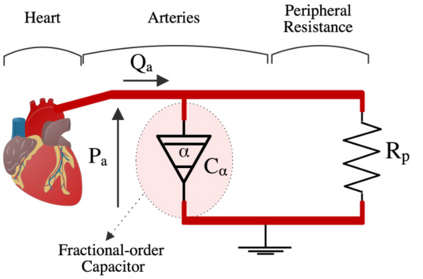
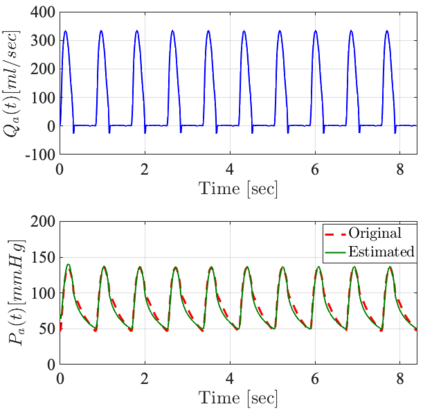
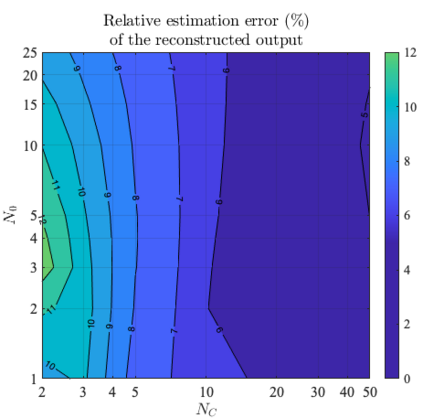
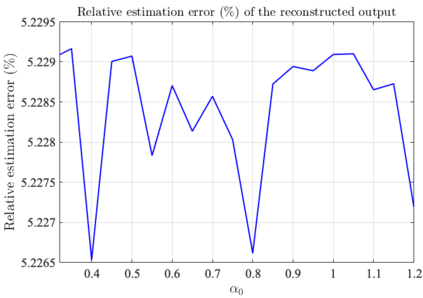
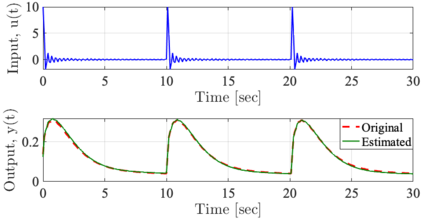
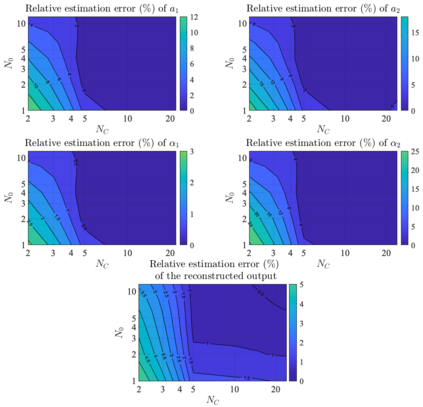
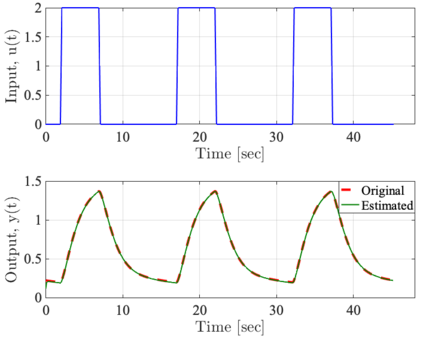
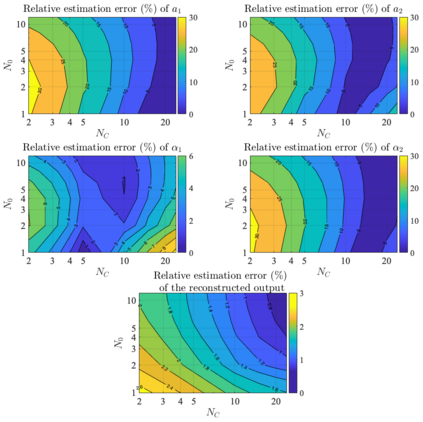
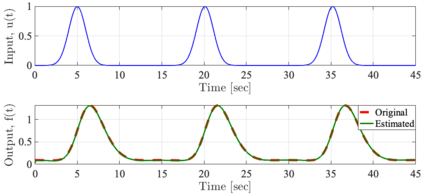
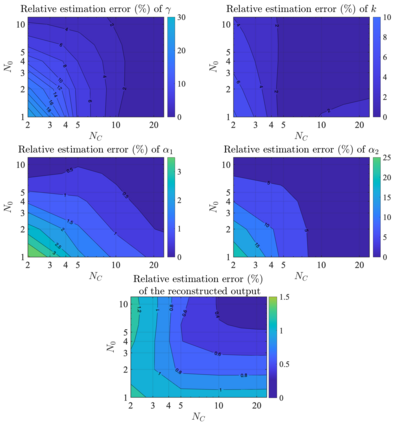
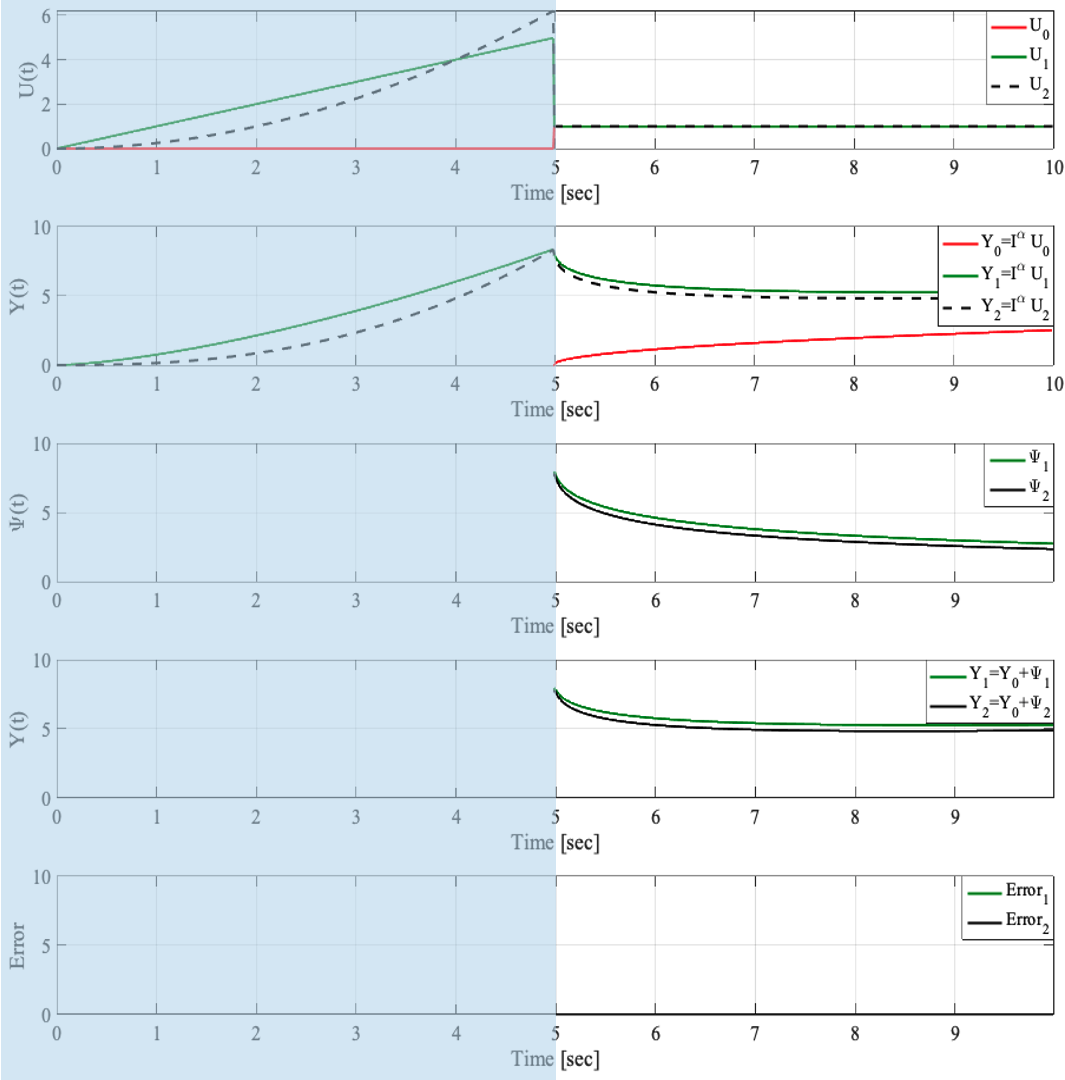
It has been recognized that using time-varying initialization functions to solve the initial value problem of fractional-order systems (FOS) is both complex and essential in defining the dynamical behavior of the states of FOSs. In this paper, we investigate the use of the initialization functions for the purpose of estimating unknown parameters of linear non-commensurate FOSs. In particular, we propose a novel "pre-initial" process that describes the dynamic characteristic of FOSs before the initial state and consists of designing an appropriate time-varying initialization function that ensures accurate convergence of the estimates of the unknown parameters. To do so, we propose an estimation technique that consists of two steps: (i) to design of practical initialization function that is output-dependent and which is employed; (ii) to solve the joint estimation problem of both parameters and fractional differentiation orders (FDOs). A convergence proof has been presented. The performance of the proposed method is illustrated through different numerical examples. Potential applications of the algorithm to joint estimation of parameters and FDOs of the fractional arterial Windkessel and neurovascular models are also presented using both synthetic and real data. The added value of the proposed "pre-initial" process to solve the studied estimation problem is shown through different simulation tests that investigate the sensitivity of estimation results using different time-varying initialization functions.
翻译:人们已经认识到,使用时间变化初始化功能来解决分序系统的初始值问题,对于确定分序系统的状态的动态行为来说,既复杂又重要。在本文件中,我们调查初始化功能的使用情况,以便估计线性非对称型FOS的未知参数。特别是,我们提出了一个新的“初始”程序,描述FOS在初始状态之前的动态特征,包括设计一个适当的时间变化初始化功能,以确保对未知参数的估计数的准确一致。为此,我们提出一种估算技术,包括两个步骤:(一) 设计实际初始化功能,该功能取决于产出,并采用这一功能;(二) 解决参数和分级分级命令的未知参数(FDOs)的联合估算问题。我们提出了一种趋同证据,通过不同的数字示例来说明拟议方法的性能。算法在联合估算参数和FDOs中的潜在应用,以确保未知参数的估计数准确趋同。为了做到这一点,我们建议采用两种步骤:(一) 设计实际初始初始初始化功能;(二) 使用不同的合成和模拟测算结果,通过不同的测算法来展示“通过不同的测算结果”。