Broken Neural Scaling Laws

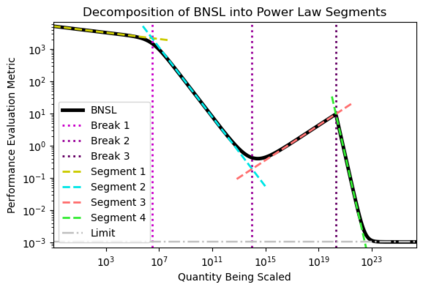
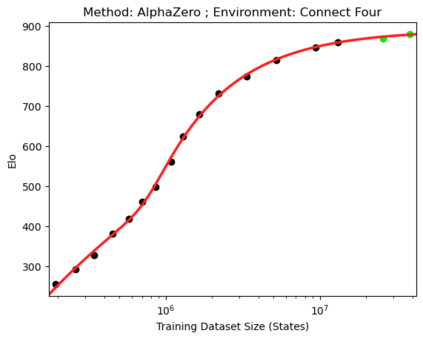
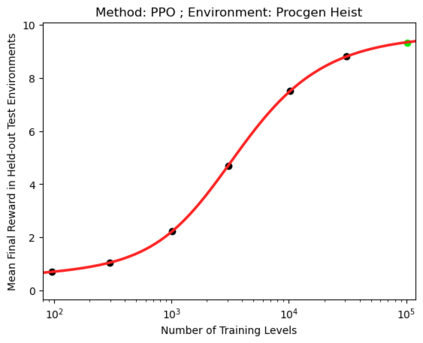
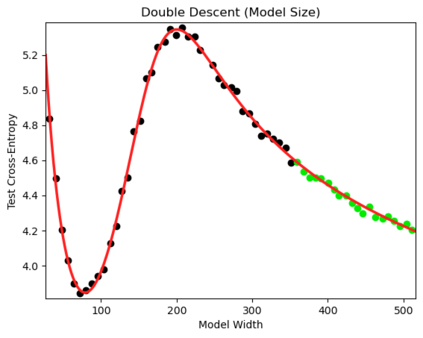
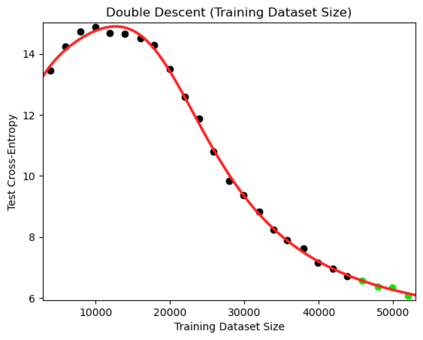
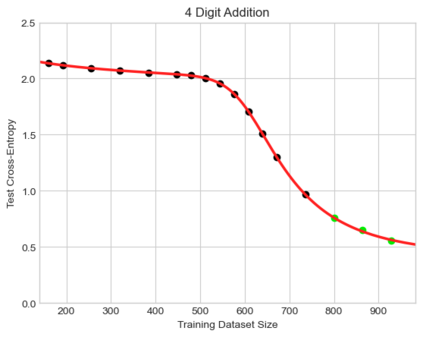
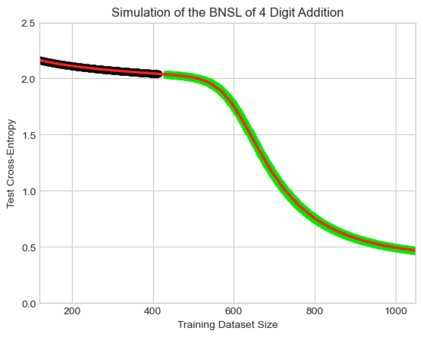
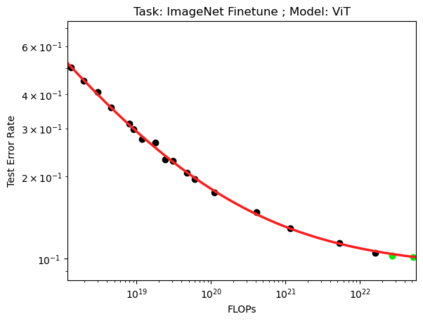
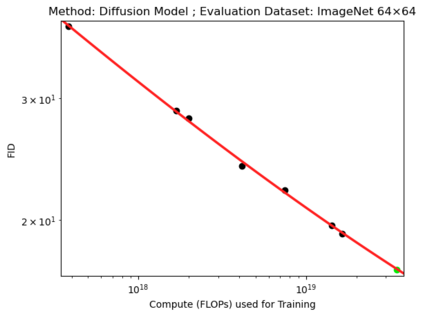
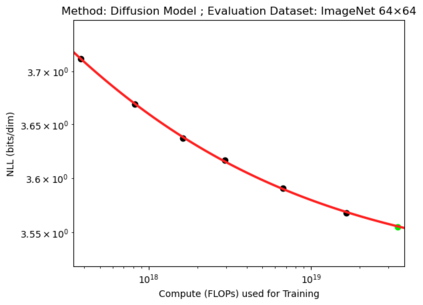
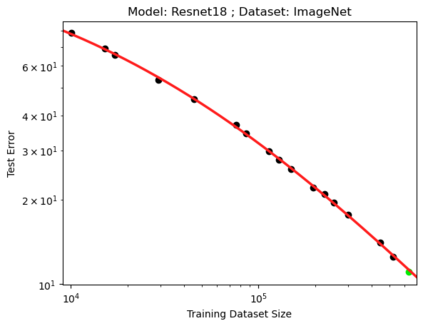
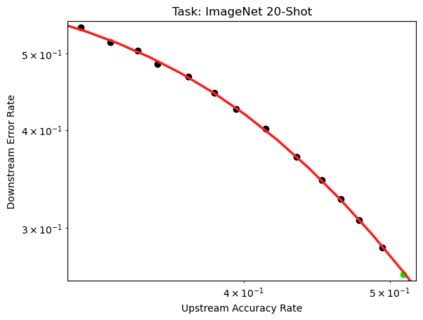
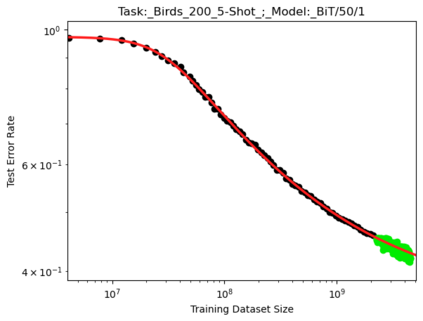
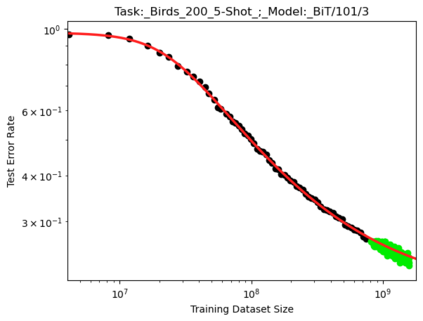
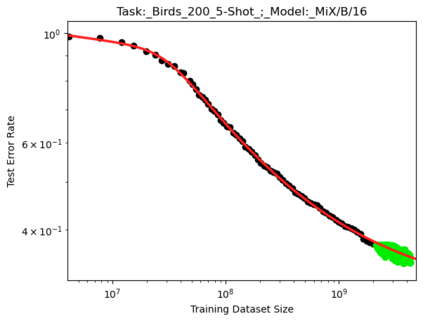
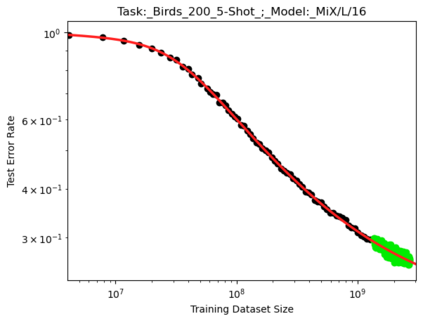
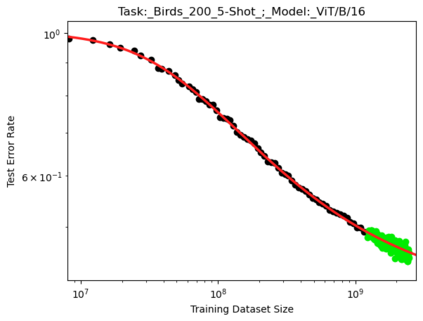
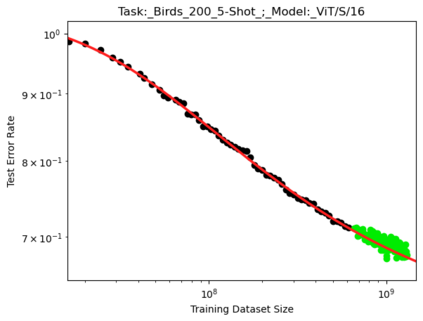
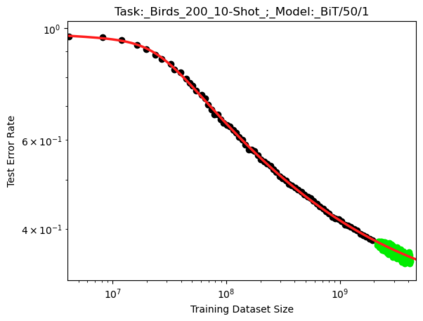
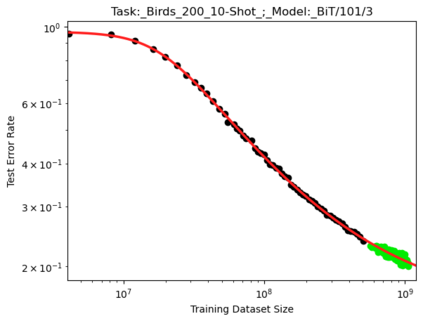
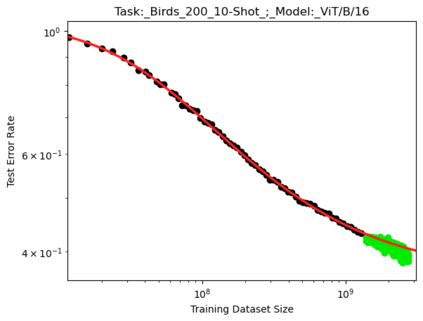
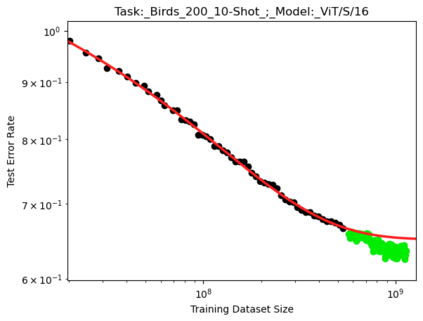
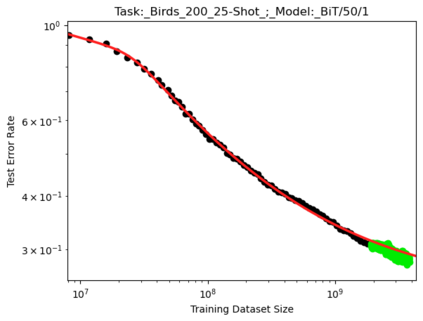
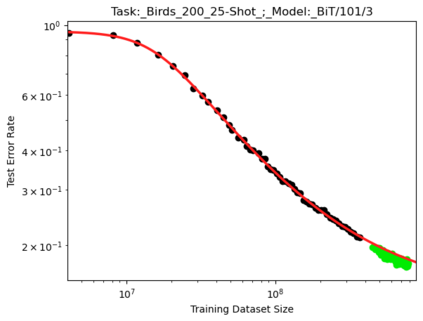
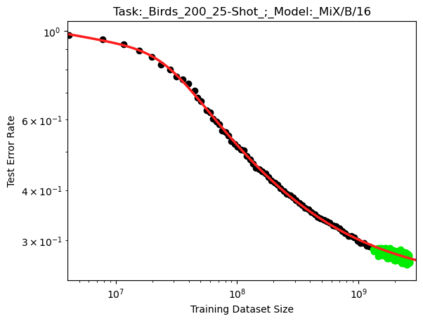
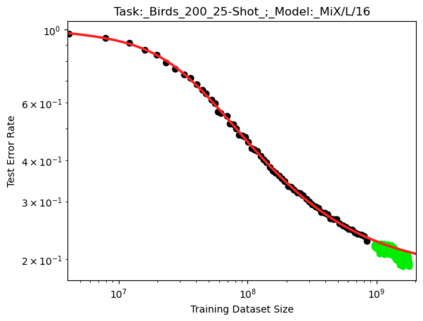
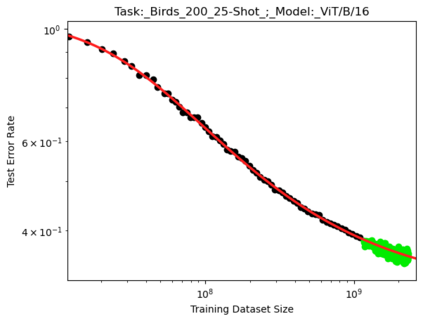
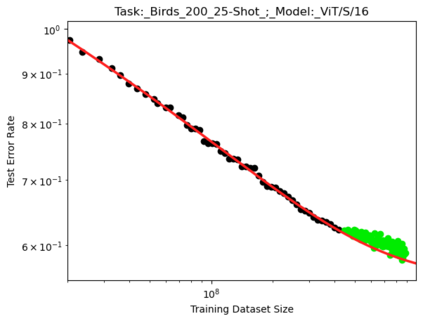
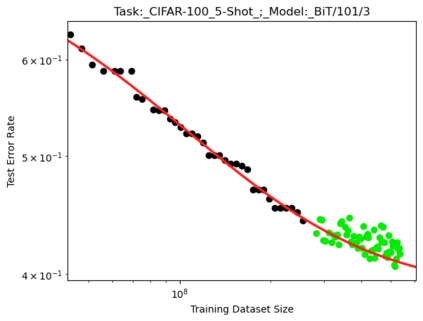
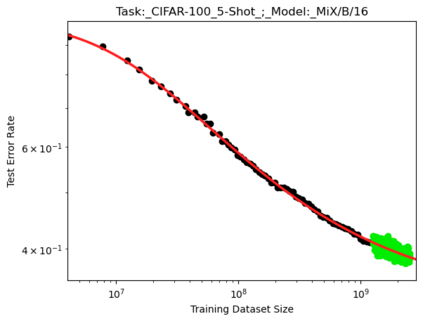
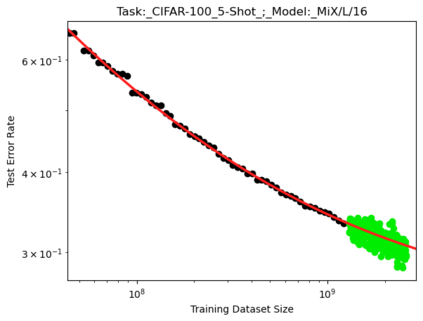
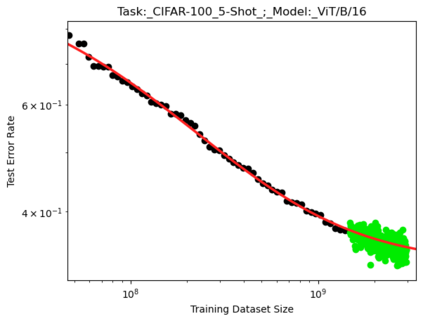
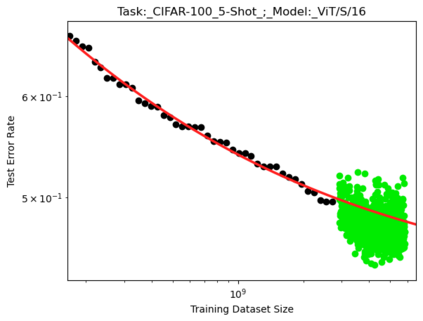
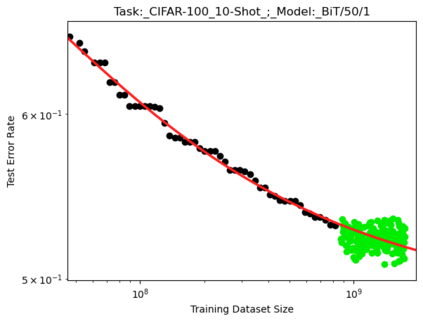
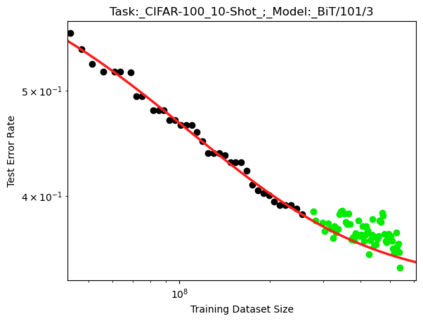
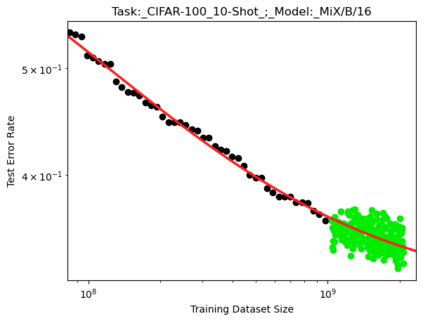
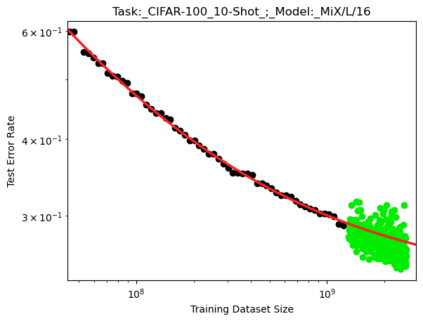
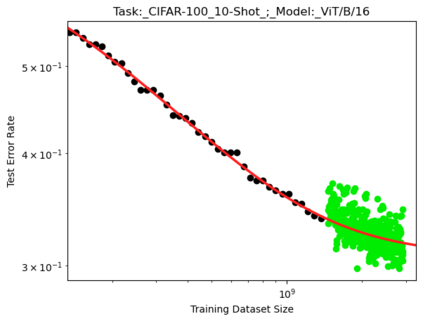
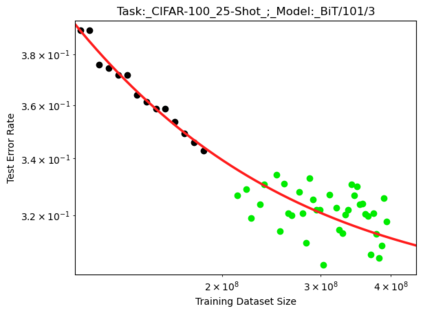
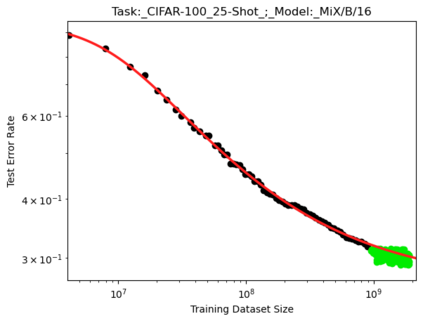
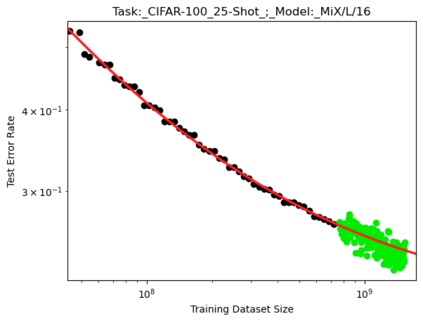
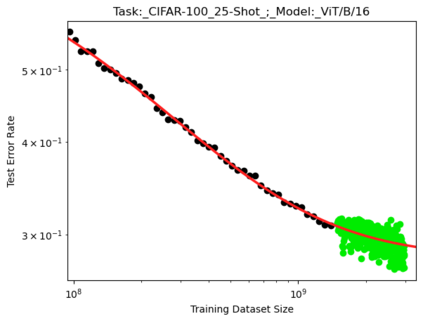
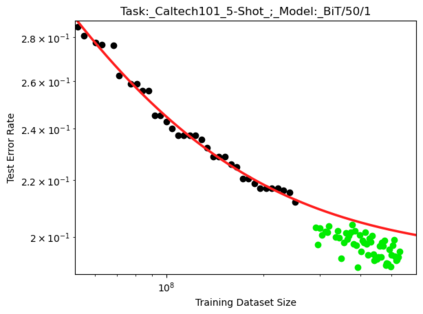
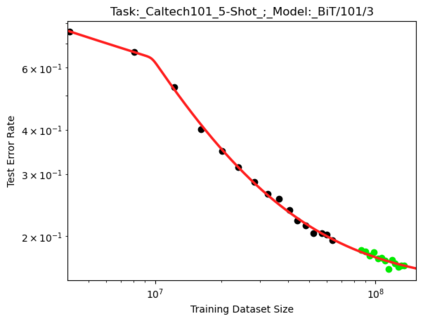
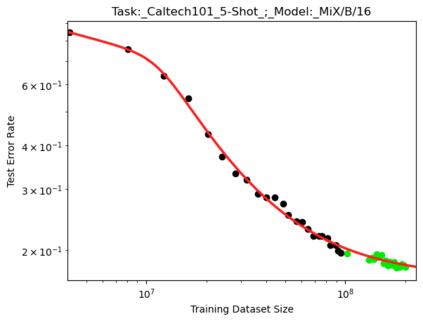
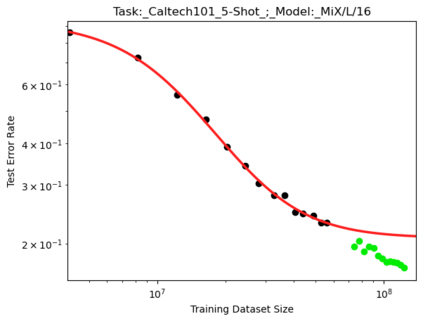
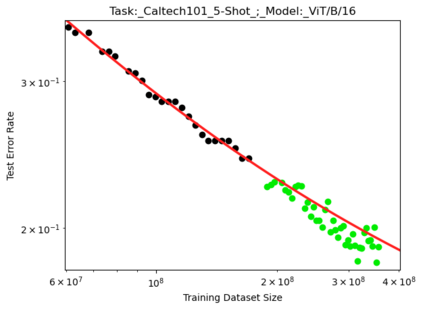
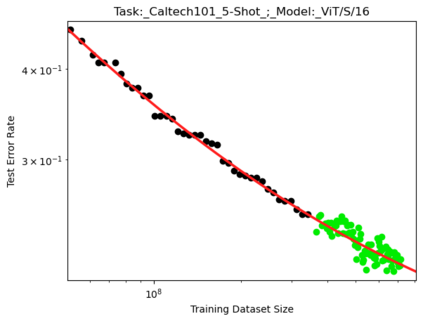
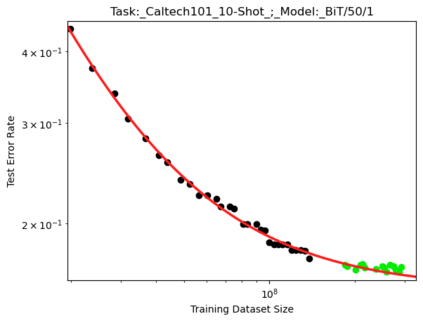
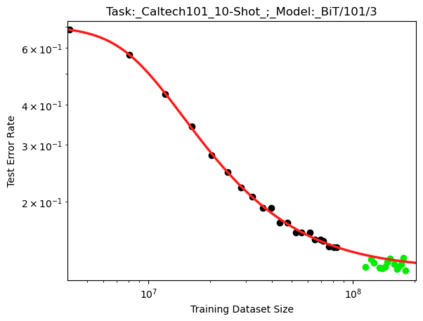
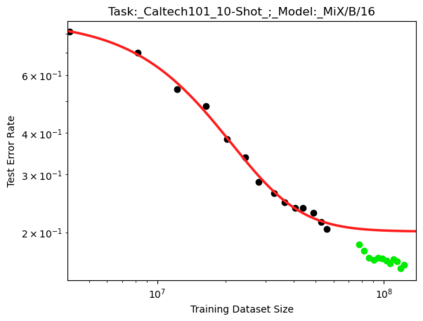
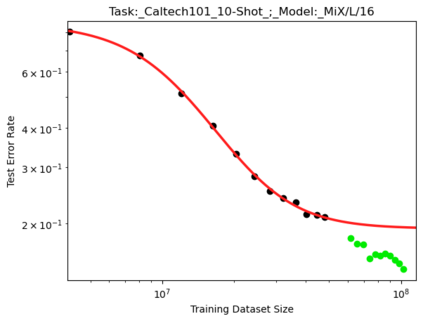
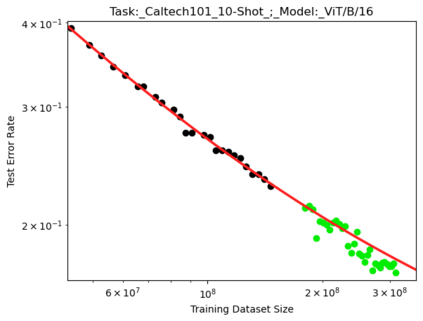
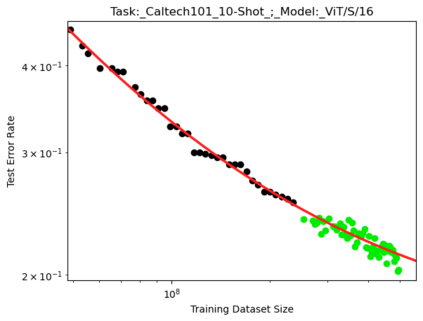
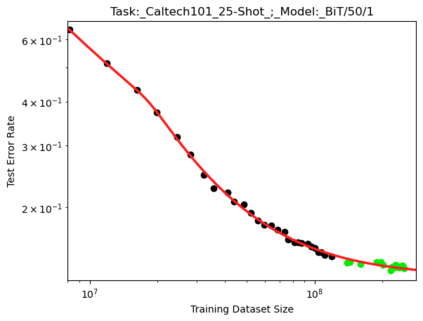
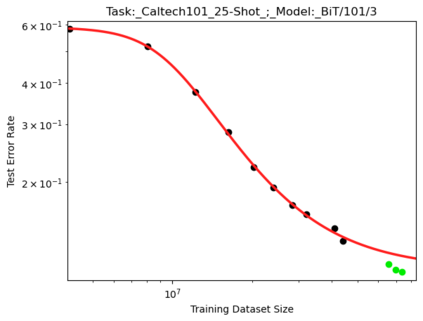
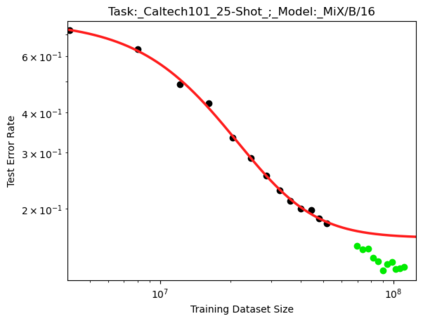
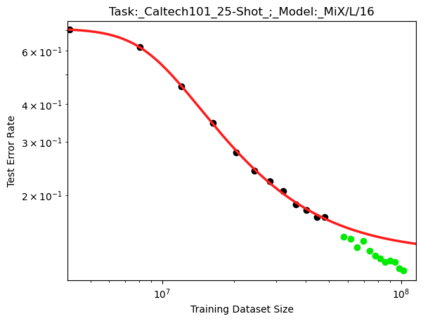
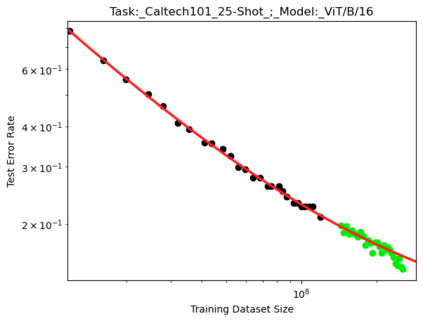
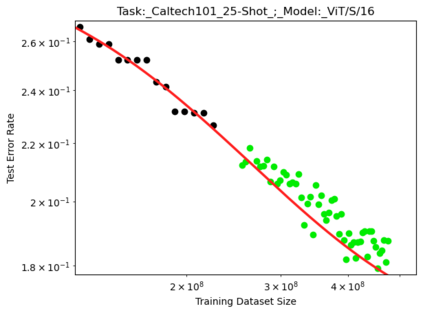
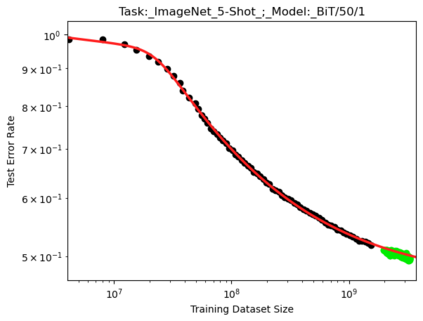
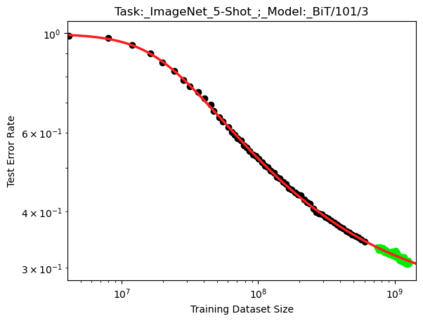
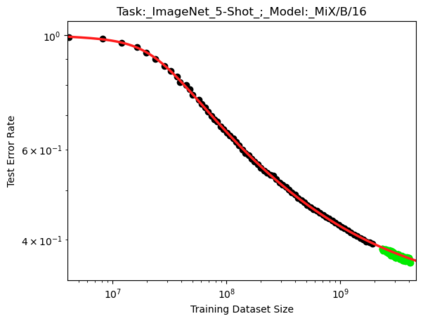
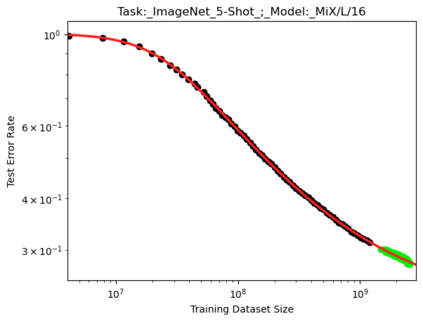
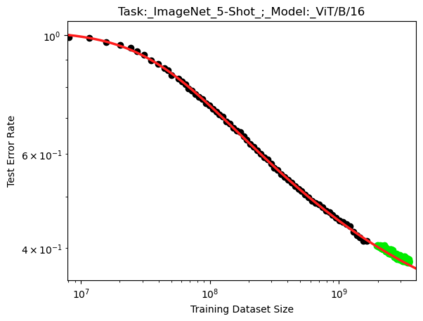
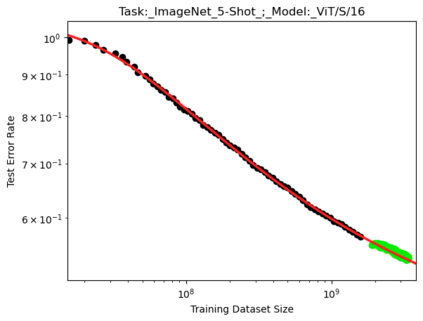
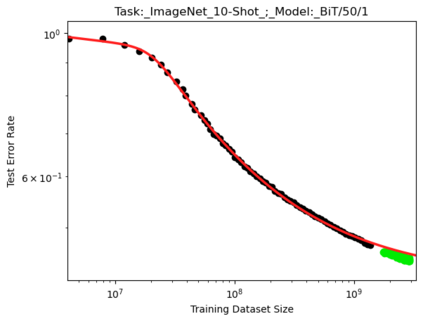
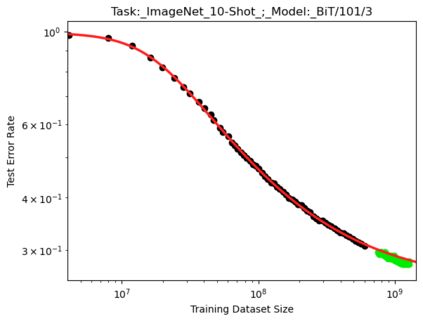
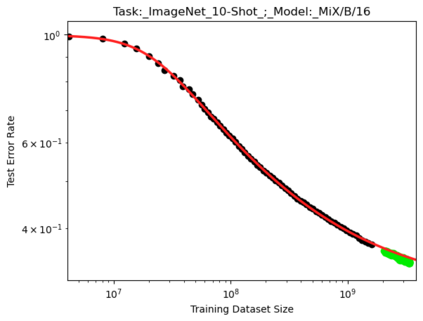
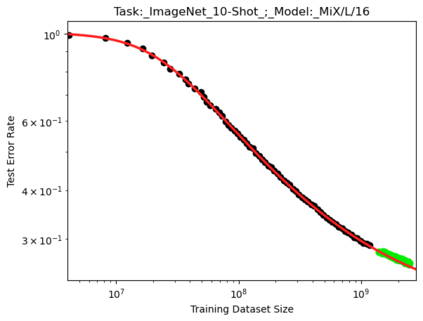
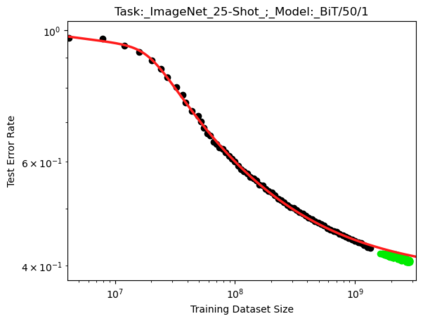
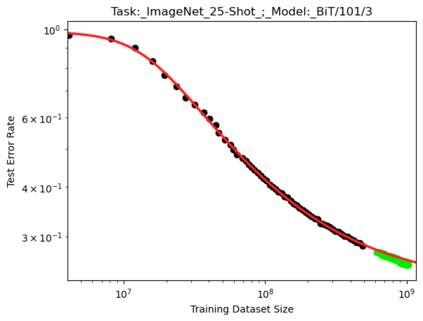
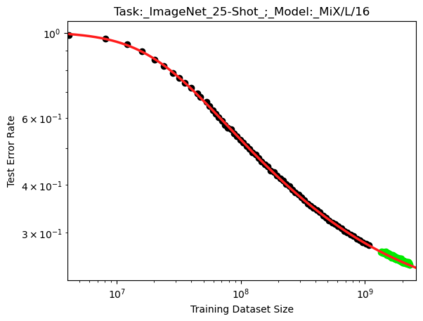
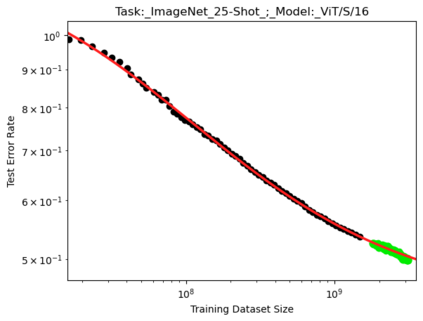
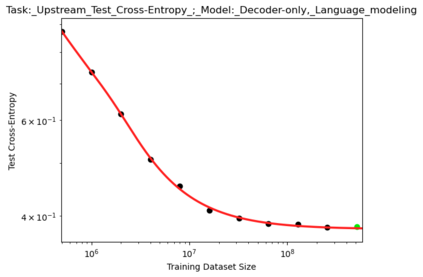
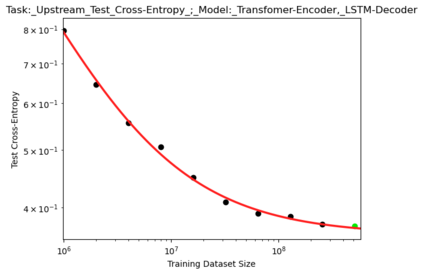
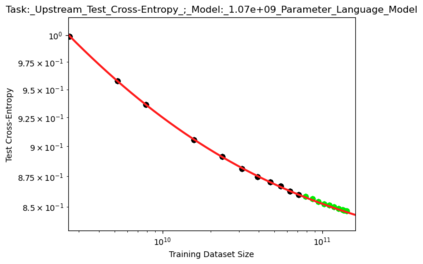
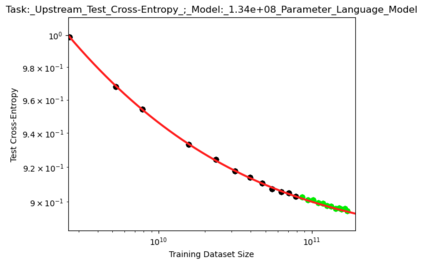
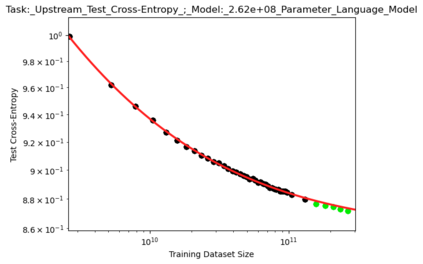
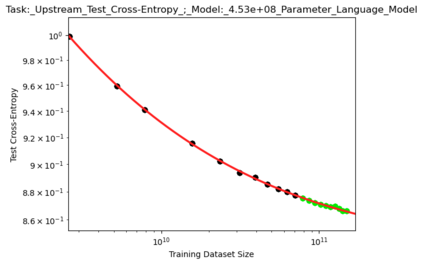
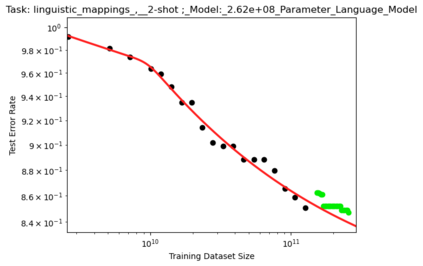
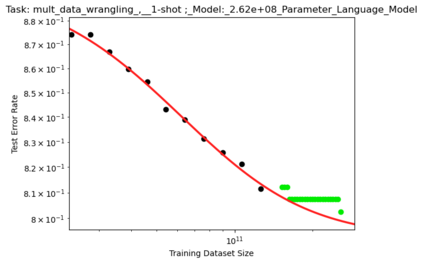
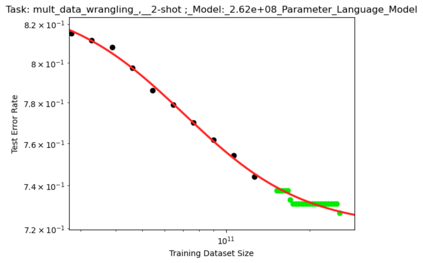
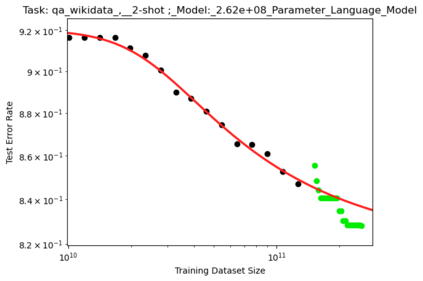
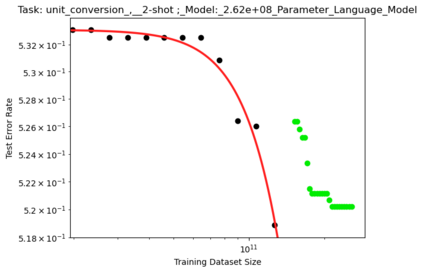
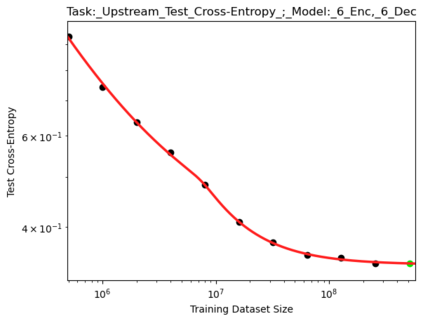
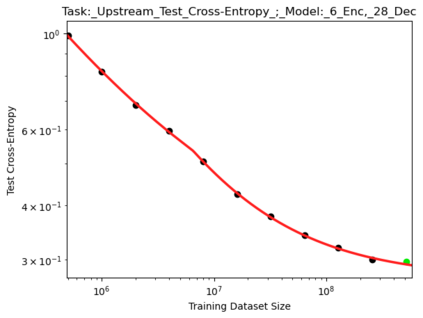
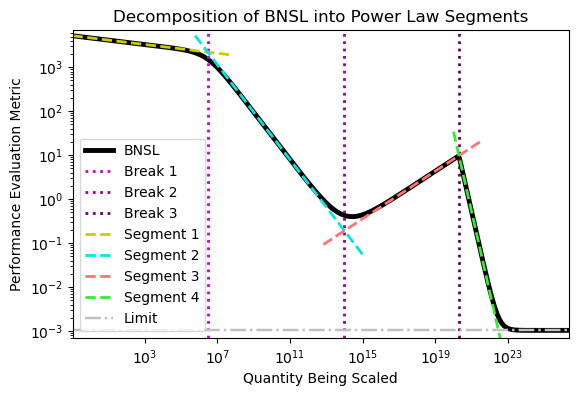
We present a smoothly broken power law functional form that accurately models and extrapolates the scaling behaviors of deep neural networks (i.e. how the evaluation metric of interest varies as the amount of compute used for training, number of model parameters, training dataset size, or upstream performance varies) for each task within a large and diverse set of upstream and downstream tasks, in zero-shot, prompted, and fine-tuned settings. This set includes large-scale vision and unsupervised language tasks, diffusion generative modeling of images, arithmetic, and reinforcement learning. When compared to other functional forms for neural scaling behavior, this functional form yields extrapolations of scaling behavior that are considerably more accurate on this set. Moreover, this functional form accurately models and extrapolates scaling behavior that other functional forms are incapable of expressing such as the non-monotonic transitions present in the scaling behavior of phenomena such as double descent and the delayed, sharp inflection points present in the scaling behavior of tasks such as arithmetic. Lastly, we use this functional form to glean insights about the limit of the predictability of scaling behavior. Code is available at https://github.com/ethancaballero/broken_neural_scaling_laws