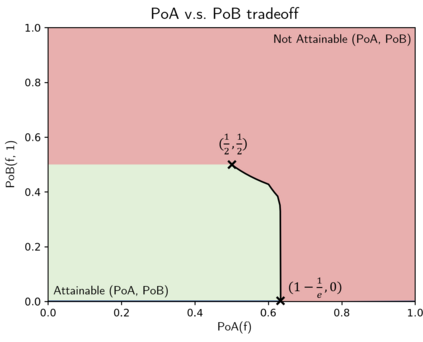
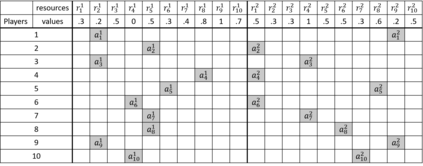
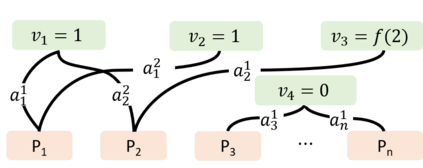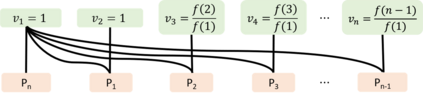Game theoretic approaches have gained traction as robust methodologies for designing distributed local algorithms that induce a desired overall system configuration in multi-agent settings. However, much of the emphasis in these approaches is on providing asymptotic guarantees on the performance of a network of agents, and there is a gap in the study of efficiency guarantees along transients of these distributed algorithms. Therefore, in this paper, we study the transient efficiency guarantees of a natural game-theoretic algorithm in the class of set covering games, which have been used to model a variety of applications. Our main results characterize the optimal utility design that maximizes the guaranteed efficiency along the transient of the natural dynamics. Furthermore, we characterize the Pareto-optimal frontier with regards to guaranteed efficiency in the transient and the asymptote under a class of game-theoretic designs. Surprisingly, we show that there exists an extreme trade-off between the long-term and short-term guarantees in that an asymptotically optimal game-theoretic design can perform arbitrarily bad in the transient.
翻译:游戏理论方法作为设计分布式本地算法的稳健方法获得了牵引力,这些算法在多试剂环境中产生了理想的整体系统配置。然而,这些方法的很多重点是为代理器网络的运行提供无线保障,在沿这些分布式算法的瞬态研究效率保障方面存在差距。因此,在本文中,我们研究了一套套装游戏中自然游戏理论算法的短暂效率保障,这些算法被用于模拟各种应用。我们的主要结果体现了在自然动态的瞬态中最大限度地实现保证效率的最佳实用设计。此外,我们把Pareto-optimal边疆定性为在一种游戏理论设计类别下保证效率。令人惊讶的是,我们发现长期和短期的保证存在着一种极端的权衡,即一种尽可能最佳的游戏理论设计在瞬变中会产生任意的坏处。