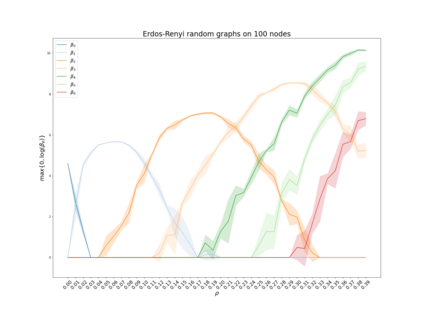
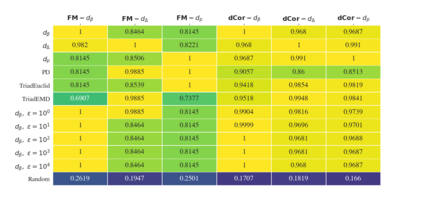
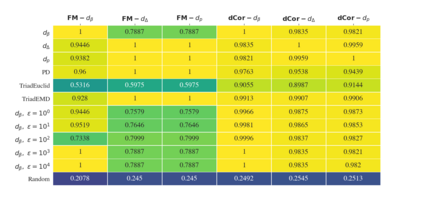
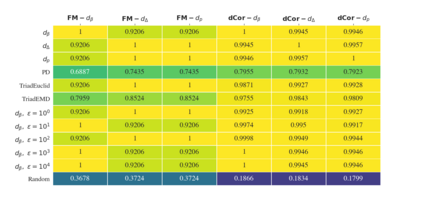
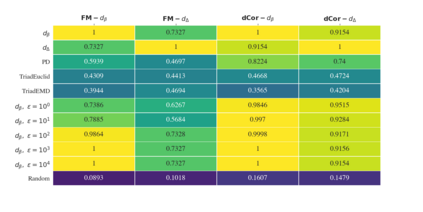
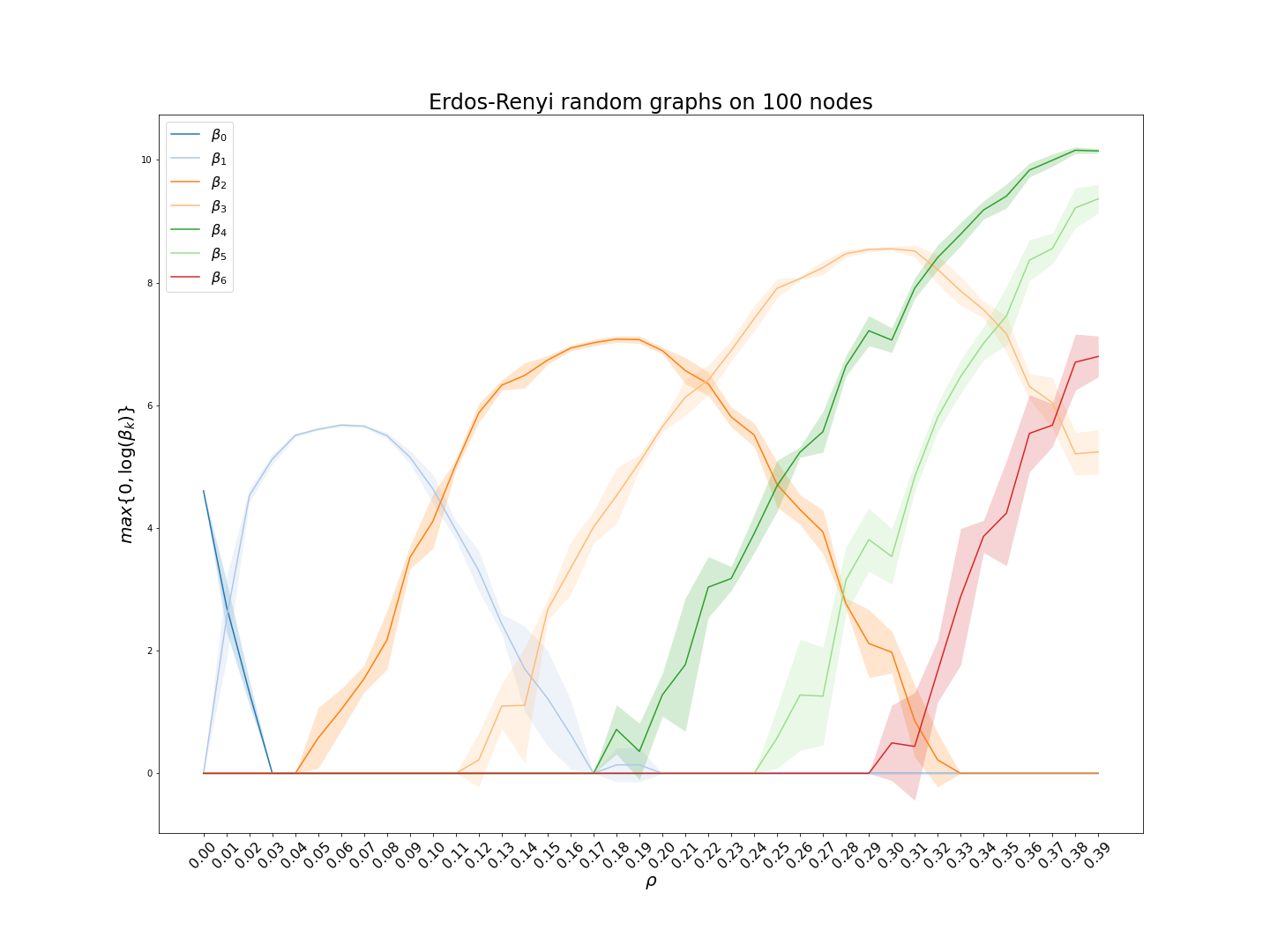
We explore pseudometrics for directed graphs in order to better understand their topological properties. The directed flag complex associated to a directed graph provides a useful bridge between network science and topology. Indeed, it has often been observed that phenomena exhibited by real-world networks reflect the topology of their flag complexes, as measured, for example, by Betti numbers or simplex counts. As it is often computationally expensive (or even unfeasible) to determine such topological features exactly, it would be extremely valuable to have pseudometrics on the set of directed graphs that can both detect the topological differences and be computed efficiently. To facilitate work in this direction, we introduce methods to measure how well a graph pseudometric captures the topology of a directed graph. We then use these methods to evaluate some well-established pseudometrics, using test data drawn from several families of random graphs.
翻译:我们探索定向图形的假度数,以便更好地了解其地形特性。与定向图形相关的定向旗帜综合体提供了网络科学和地形学之间的有用桥梁。事实上,人们经常发现,真实世界网络展示的现象反映了其国旗复合体的地形学,例如用贝蒂数字或简单x计数测量。由于精确确定此类地形特征的计算成本通常很高(甚至不可行),因此,在定向图集上安装既能检测地形差异又能有效计算的伪度值是非常有价值的。为了便利这方面的工作,我们采用方法测量图形伪度如何很好地捕捉定向图形的地形学。然后,我们使用这些方法,利用从几组随机图中提取的测试数据,评估一些成熟的伪度。