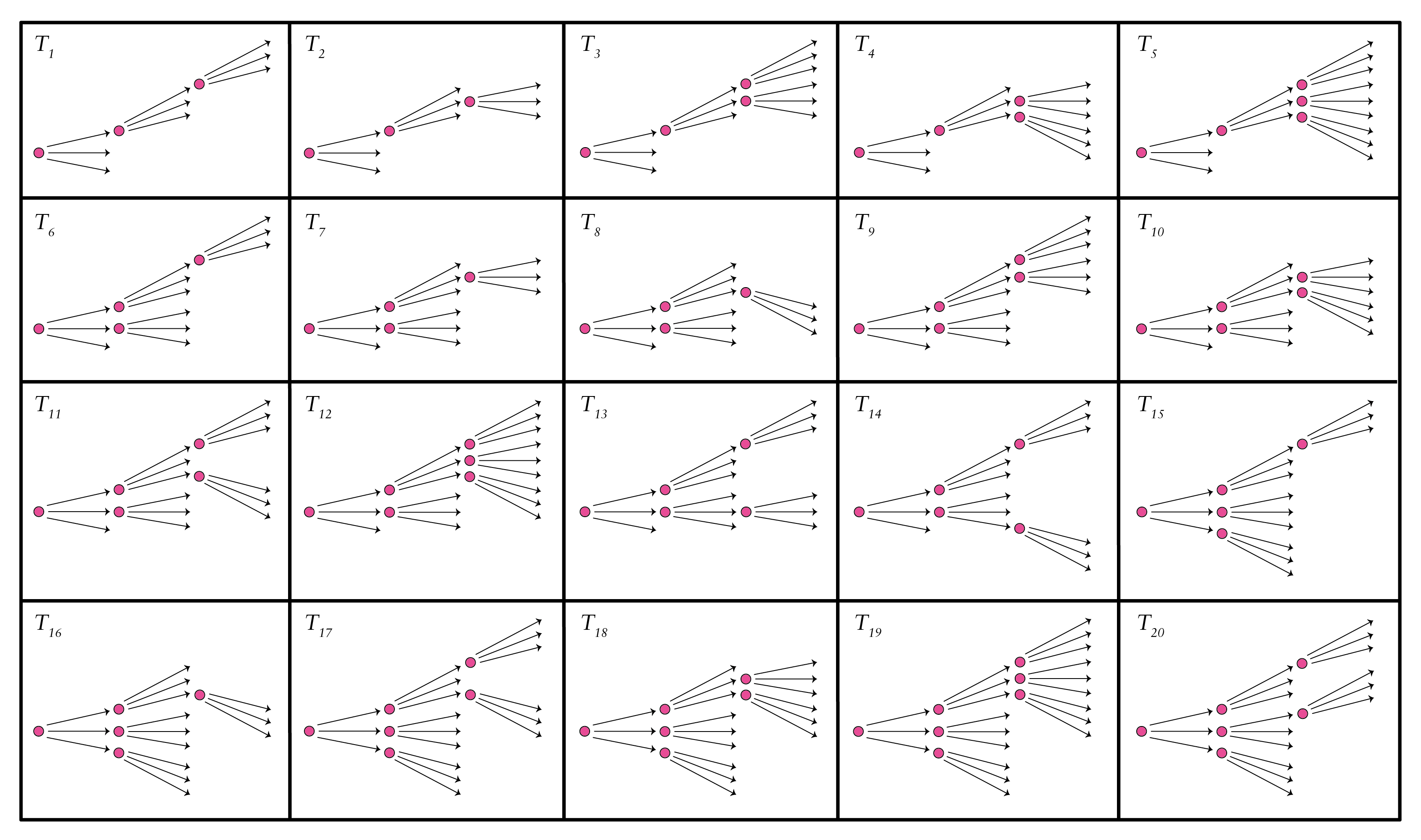
A staged tree model is a discrete statistical model encoding relationships between events. These models are realised by directed trees with coloured vertices. In algebro-geometric terms, the model consists of points inside a toric variety. For certain trees, called balanced, the model is in fact the intersection of the toric variety and the probability simplex. This gives the model a straightforward description, and has computational advantages. In this paper we show that the class of staged tree models with a toric structure extends far outside of the balanced case, if we allow a change of coordinates. It is an open problem whether all staged tree models have toric structure.
翻译:阶梯树模型是不同事件之间独立的统计模型编码关系。 这些模型是通过带色脊椎的定向树实现的。 在藻类- 几何学术语中, 模型由一丁种内的点组成。 对于某些树木来说, 称为平衡, 模型实际上是托理品种和概率简单x的交叉点。 这给模型提供了直截了当的描述, 并具有计算优势。 在本文中, 如果允许改变坐标的话, 我们可以看到带有极分结构的阶梯树模型的类别远远超出平衡情况的范围。 是否所有阶梯树模型都具有托理结构, 是一个开放的问题 。