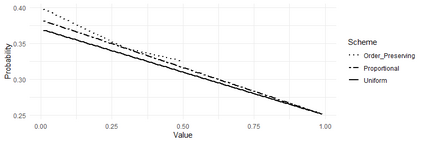
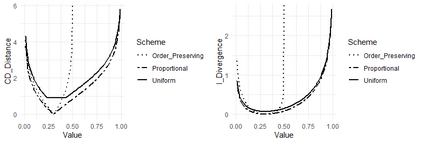
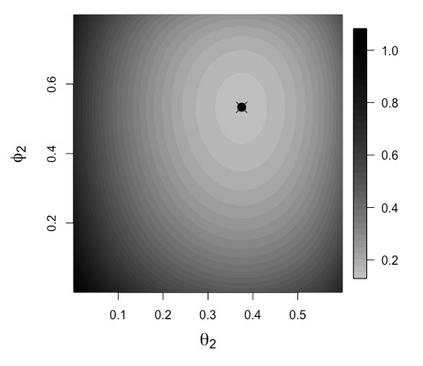
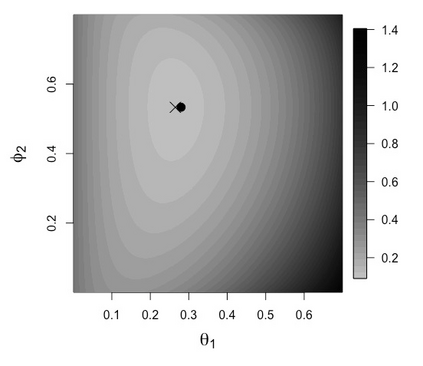
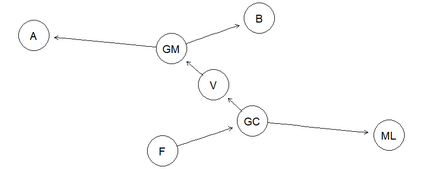
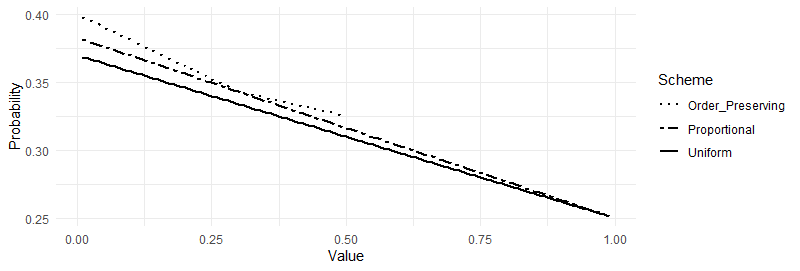
Sensitivity analysis in probabilistic discrete graphical models is usually conducted by varying one probability value at a time and observing how this affects output probabilities of interest. When one probability is varied then others are proportionally covaried to respect the sum-to-one condition of probability laws. The choice of proportional covariation is justified by a variety of optimality conditions, under which the original and the varied distributions are as close as possible under different measures of closeness. For variations of more than one parameter at a time proportional covariation is justified in some special cases only. In this work, for the large class of discrete statistical models entertaining a regular monomial parametrisation, we demonstrate the optimality of newly defined proportional multi-way schemes with respect to an optimality criterion based on the notion of I-divergence. We demonstrate that there are varying parameters choices for which proportional covariation is not optimal and identify the sub-family of model distributions where the distance between the original distribution and the one where probabilities are covaried proportionally is minimum. This is shown by adopting a new formal, geometric characterization of sensitivity analysis in monomial models, which include a wide array of probabilistic graphical models. We also demonstrate the optimality of proportional covariation for multi-way analyses in Naive Bayes classifiers.
翻译:对概率离散图形模型的感知性分析通常以不同概率值进行,同时观察它如何影响产值的概率概率。当一种概率变化时,其他概率则按比例相异,以尊重概率法的总和至一条件。选择比例共变法有多种最佳性条件,在这种条件下,原始和不同分布在接近度的不同测量中尽可能接近。如果在某种特殊情况下,在比例共变法有合理理由时,一个以上参数的变异,则只对比例相异性进行观察。在这项工作中,对定期单一比对法的大型离散统计模型而言,我们展示了新定义的成比例成比例多行法计划的最佳性,以基于I比差度概念的最佳性标准为根据。我们证明,有各种不同的参数选择,在这种选择中,在比例相近性变法中,在原始分布和概率相异性比较的距离最小的情况下,确定模型分布的次组合。对于定期单一比对等化的大型离异性统计模型,我们通过采用新的正式的、比例比重的多行模型来显示最佳比度的分辨率分析,以展示多度的分辨率分析。