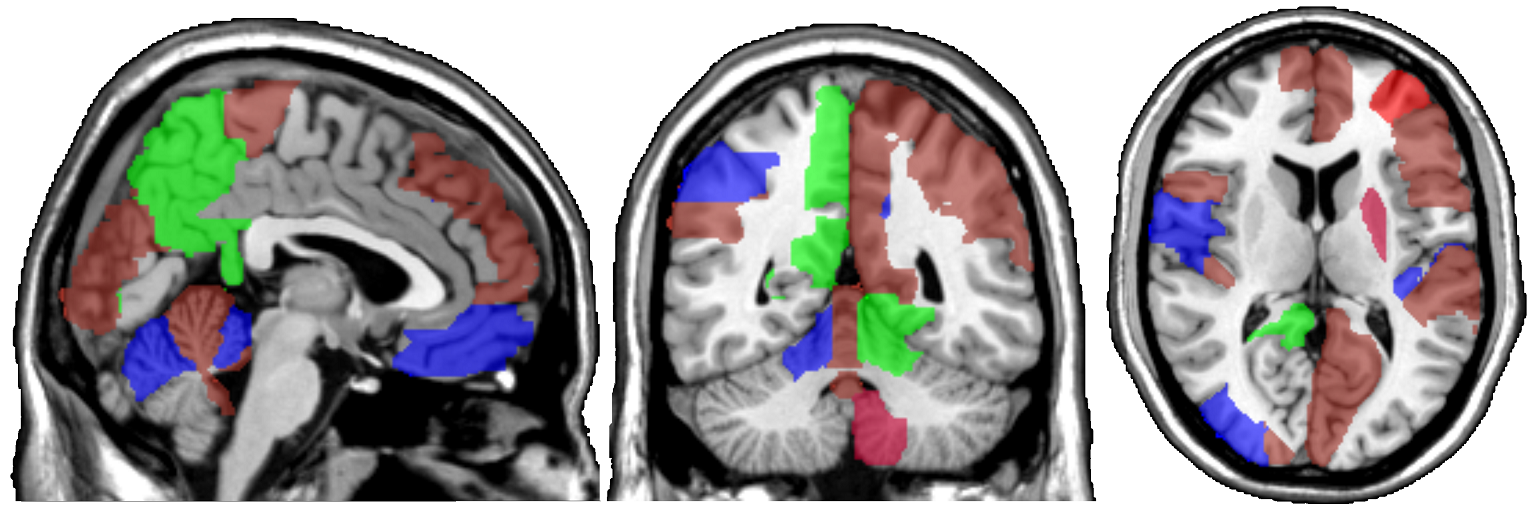
In this paper, we propose methods for functional predictor selection and the estimation of smooth functional coefficients simultaneously in a scalar-on-function regression problem under high-dimensional multivariate functional data setting. In particular, we develop two methods for functional group-sparse regression under a generic Hilbert space of infinite dimension. We show the convergence of algorithms and the consistency of the estimation and the selection (oracle property) under infinite-dimensional Hilbert spaces. Simulation studies show the effectiveness of the methods in both the selection and the estimation of functional coefficients. The applications to the functional magnetic resonance imaging (fMRI) reveal the regions of the human brain related to ADHD and IQ.
翻译:在本文中,我们在高维多变量功能数据设置下,提出功能预测器选择方法和平稳功能系数估算方法,同时提出在功能回归问题中,在高维多变量功能数据设置下,同时提出功能预测器选择和平稳功能系数估算方法,特别是,我们为功能群状回归开发了两种方法,在通用的无限范围的Hilbert空间下,我们展示了算法的趋同以及无限维度希尔伯特空间下估算和选择(孔径属性)的一致性。模拟研究显示了功能系数选择和估算方法的有效性。对功能磁共振成像(fMRI)的应用揭示了与ADHD和IQ有关的人类大脑区域。