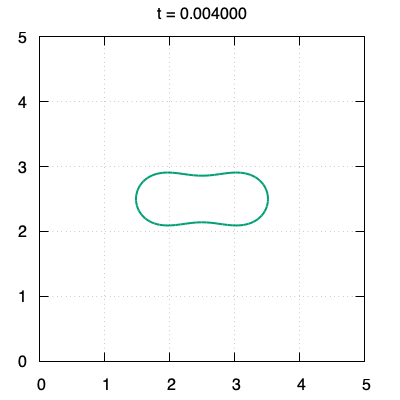
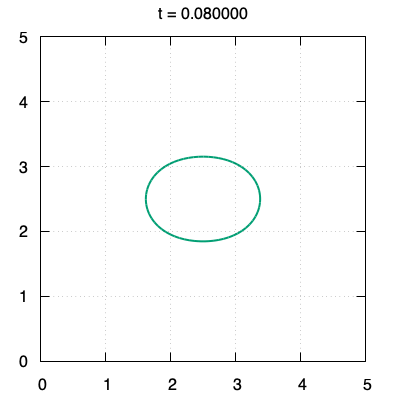
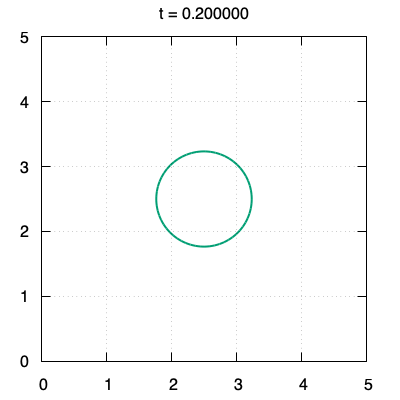
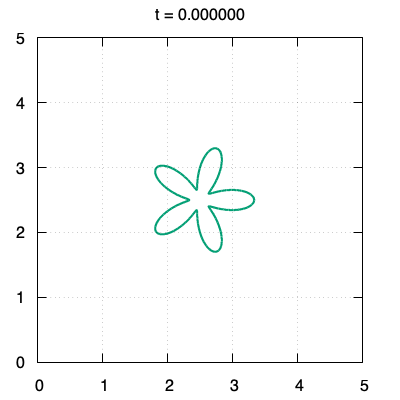
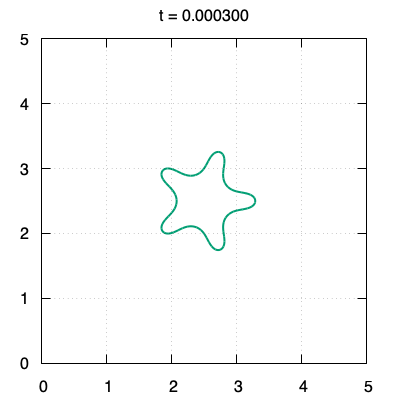
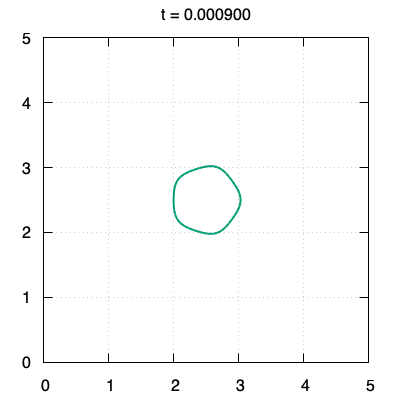
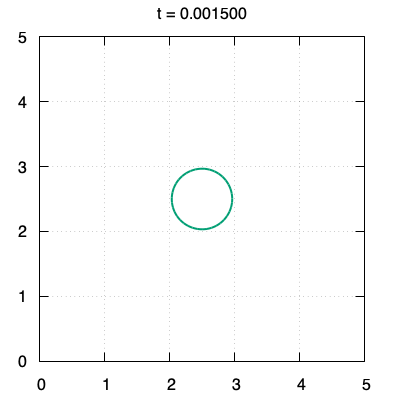
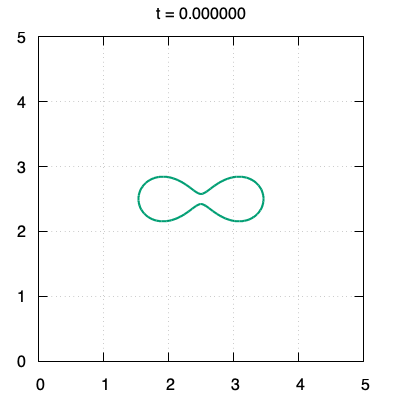
We propose a threshold-type algorithm to the $L^2$-gradient flow of the Canham-Helfrich functional generalized to $\mathbb{R}^N$. The algorithm to the Willmore flow is derived as a special case in $\mathbb{R}^2$ or $\mathbb{R}^3$. This algorithm is constructed based on an asymptotic expansion of the solution to the initial value problem for a fourth order linear parabolic partial differential equation whose initial data is the indicator function on the compact set $\Omega_0$. The crucial points are to prove that the boundary $\partial\Omega_1$ of the new set $\Omega_1$ generated by our algorithm is included in $O(t)$-neighborhood from $\partial\Omega_0$ for small time $t>0$ and to show that the derivative of the threshold function in the normal direction for $\partial\Omega_0$ is far from zero in the small time interval. Finally, numerical examples of planar curves governed by the Willmore flow are provided by using our threshold-type algorithm.
翻译:暂无翻译