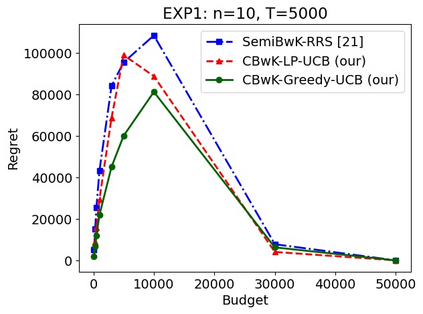
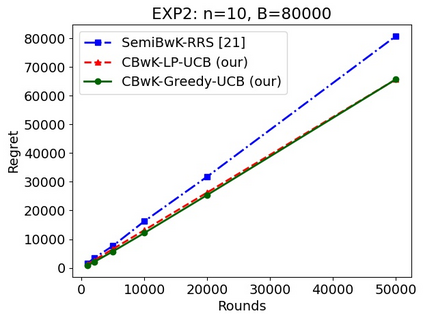
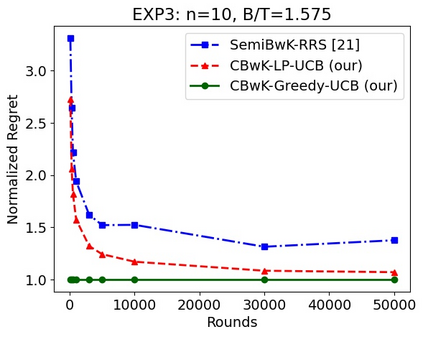
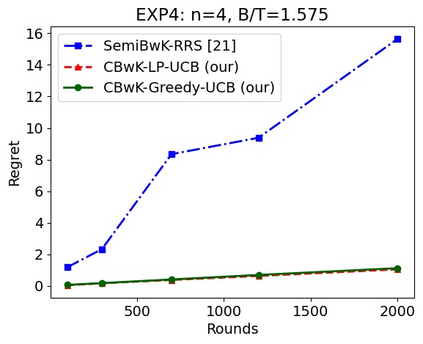
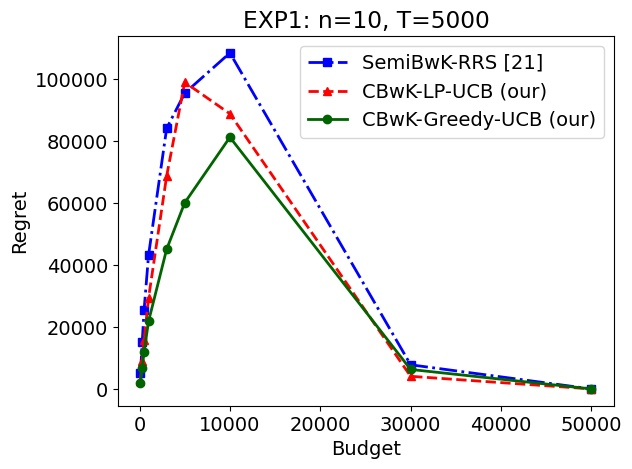
We consider a budgeted combinatorial multi-armed bandit setting where, in every round, the algorithm selects a super-arm consisting of one or more arms. The goal is to minimize the total expected regret after all rounds within a limited budget. Existing techniques in this literature either fix the budget per round or fix the number of arms pulled in each round. Our setting is more general where based on the remaining budget and remaining number of rounds, the algorithm can decide how many arms to be pulled in each round. First, we propose CBwK-Greedy-UCB algorithm, which uses a greedy technique, CBwK-Greedy, to allocate the arms to the rounds. Next, we propose a reduction of this problem to Bandits with Knapsacks (BwK) with a single pull. With this reduction, we propose CBwK-LPUCB that uses PrimalDualBwK ingeniously. We rigorously prove regret bounds for CBwK-LP-UCB. We experimentally compare the two algorithms and observe that CBwK-Greedy-UCB performs incrementally better than CBwK-LP-UCB. We also show that for very high budgets, the regret goes to zero.
翻译:我们考虑的是预算的组合式多武装土匪布局,在每一个回合中,算法选择由一个或多个武器组成的超级武器。目标是在有限的预算范围内最大限度地减少所有回合后预期的遗憾。 文献中的现有技术要么固定每回合的预算, 要么固定每回合的军火数量。 我们的设置比较一般, 以剩余预算和剩余子弹数量为基础, 算法可以决定每回合要拉多少个武器。 首先, 我们提议CBwK- Greedy- UCB算法, 使用贪婪技术, CBwK- Greedy, 将武器分配给这些回合。 下一步, 我们提议用单拉力来减少Knappsacks(BwK) 给Bandits的问题。 随着这一削减, 我们建议CBwK- LPUB, 使用PUB- LP- CUB 的精度, 我们严格证明对CB- LP- CUB 两种算法是令人遗憾的。 我们实验性地比较了CBwK- Greed- Greed- B 预算, 也比UC 高的B。