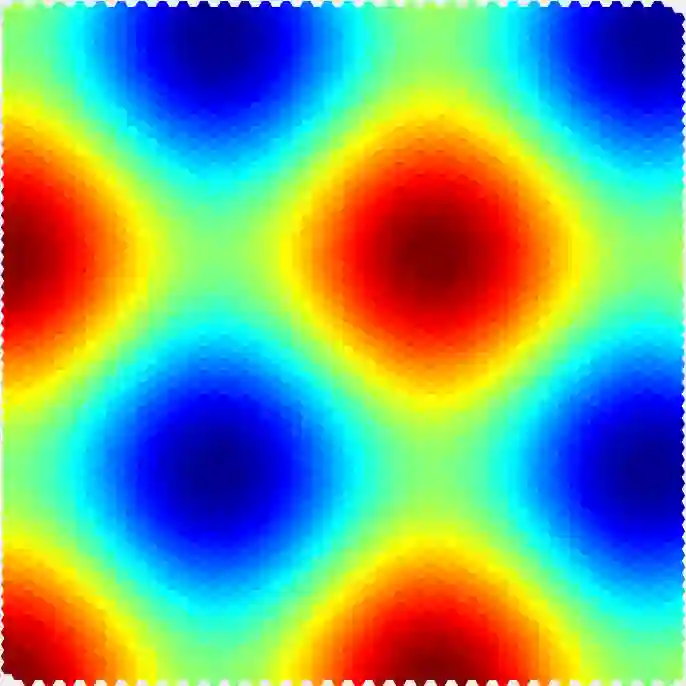
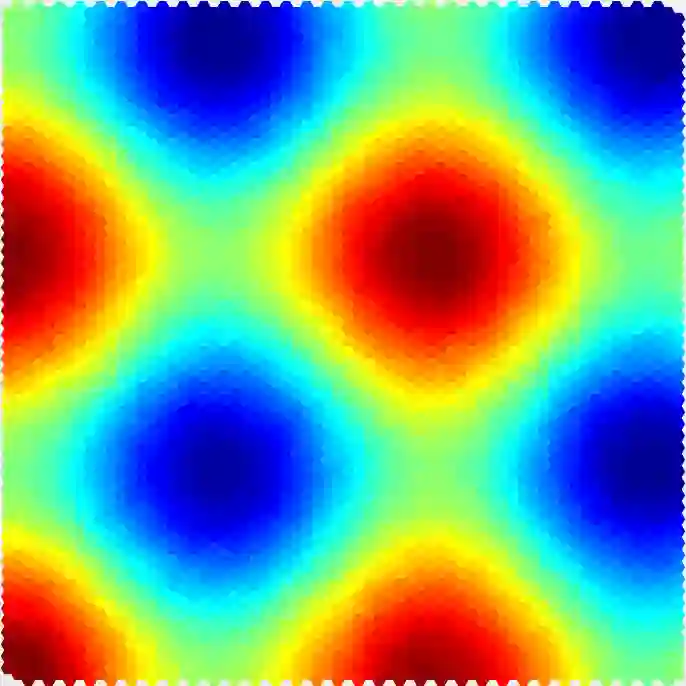
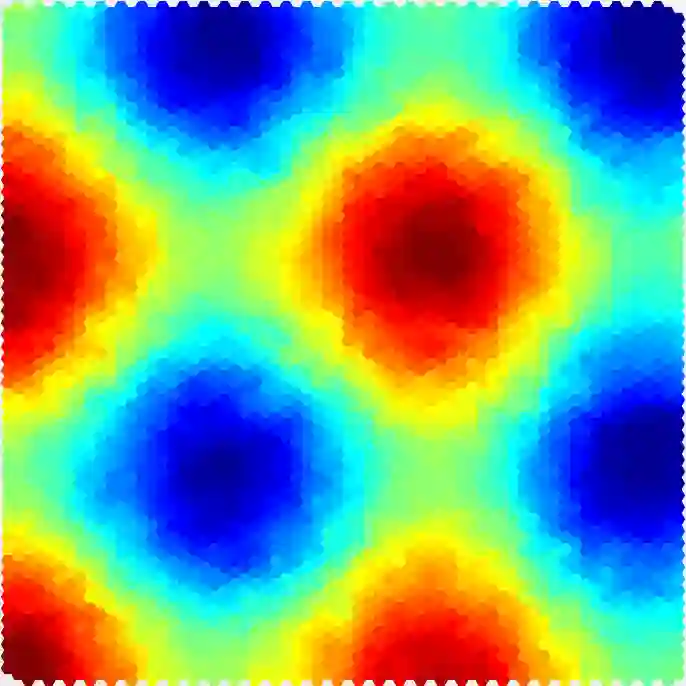
In this article, we provide stability estimates for the finite element discretization of a class of inverse parameter problems of the form $-\nabla\cdot(\mu S) = \g f$ in a domain $\Omega$ of $\R^d$. Here $\mu$ is the unknown parameter to recover, the matrix valued function $S$ and the vector valued distribution $\g f$ are known. As uniqueness is not guaranteed in general for this problem, we prove a Lipschitz-type stability estimate in an hyperplane of $L^2(\Omega)$. This stability is obtained through an adaptation of the so-called discrete \emph{inf-sup} constant or LBB constant to a large class of first-order differential operators. We then provide a simple and original discretization based on hexagonal finite element that satisfies the discrete stability condition and shows corresponding numerical reconstructions. The obtained algebraic inversion method is efficient as it does not require any iterative solving of the forward problem and is very general as it does not require any smoothness hypothesis for the data nor any additional information at the boundary.
翻译:在本篇文章中,我们为以$- nabla\ cdot( mu- s) =\ g ff f$在域$\\ omega$\ R ⁇ d$ $\ d$. 这里$\ mu$是需要回收的未知参数, 矩阵值函数值为美元, 矢量值分配值为美元 美元 。 由于一般无法保证这一问题的独特性, 我们证明, 在高平面为$L2(\\ Omega) 中, Lipschitz 类型的稳定性估算值是有效的。 这种稳定性是通过将所谓的离心值常数/ emph{ inf- sup} 常数或 LBB 常数调整到一等运算的大型类别运算符。 我们然后根据符合离心稳定性条件的六角定值元素提供简单和原始的离心值, 并显示相应的数字重建。 获得的代数转换法是有效的, 因为它不需要前期问题的任何迭接合解决, 而且非常笼统,因为它不需要任何平滑的边界假设或任何其他信息。