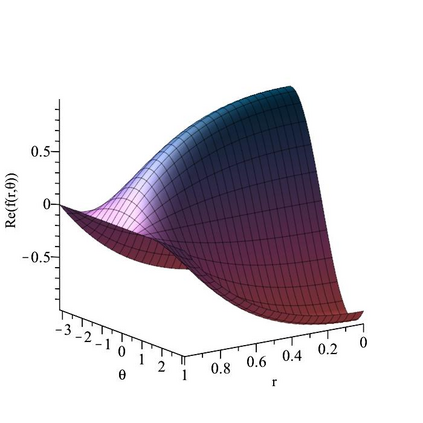
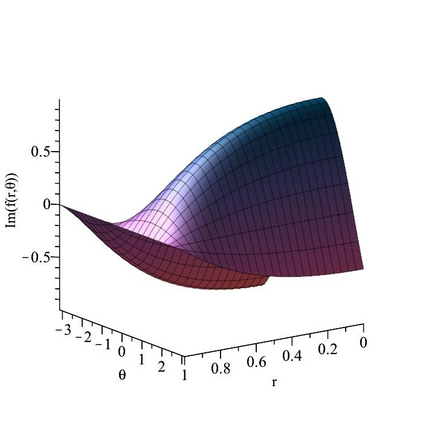
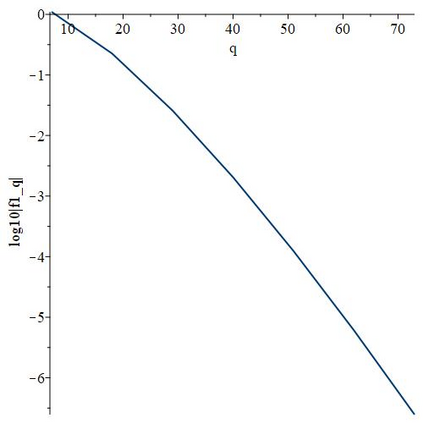
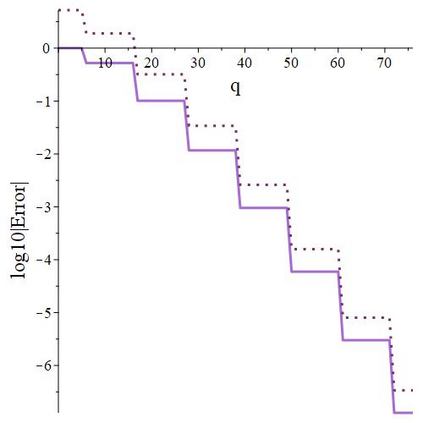
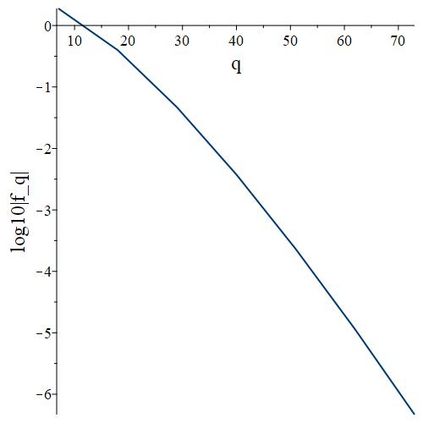
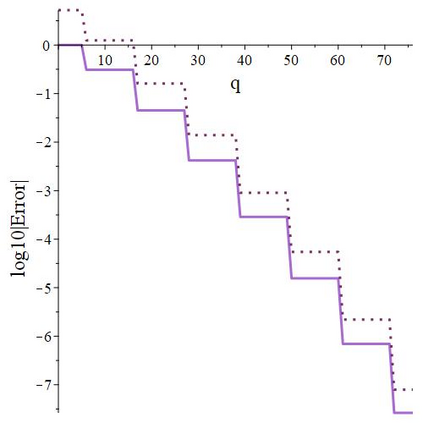
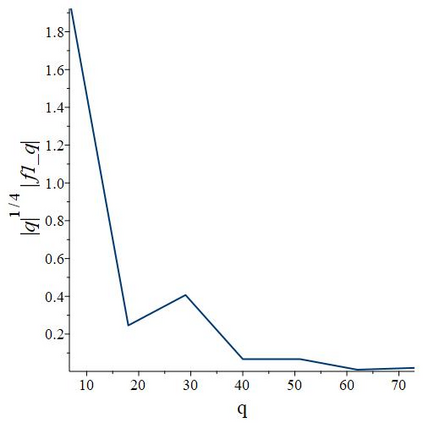
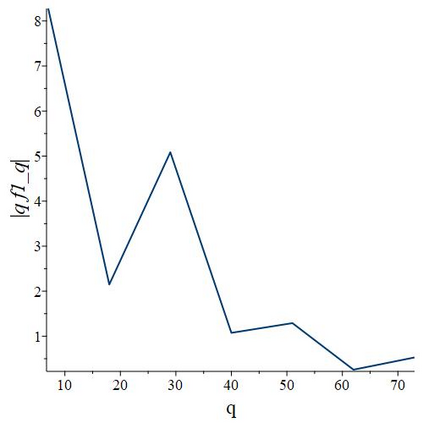
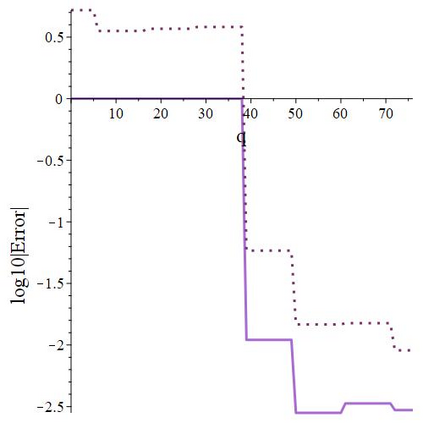
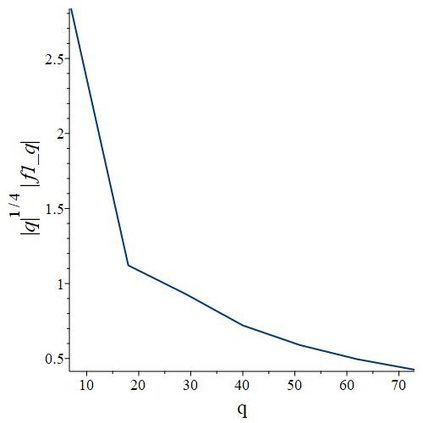
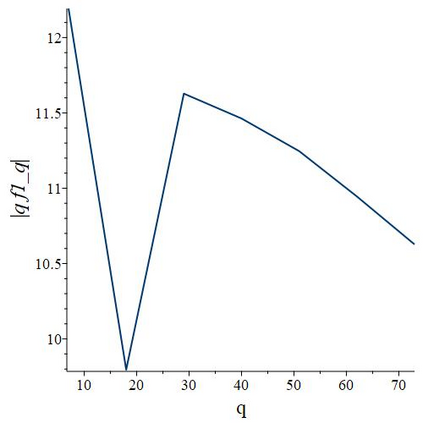
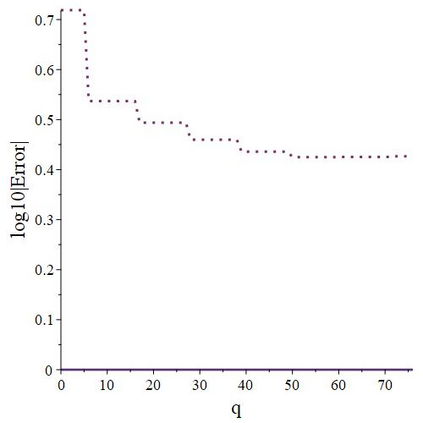
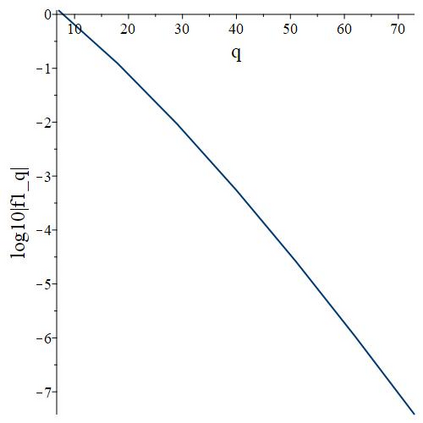
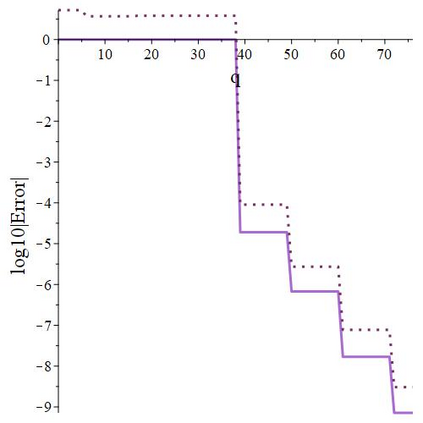
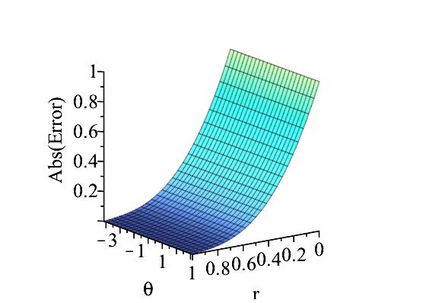
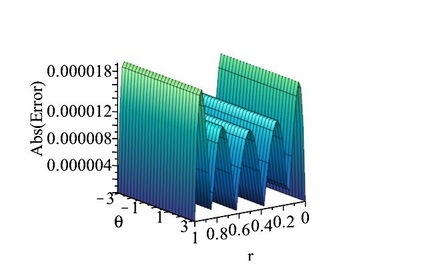
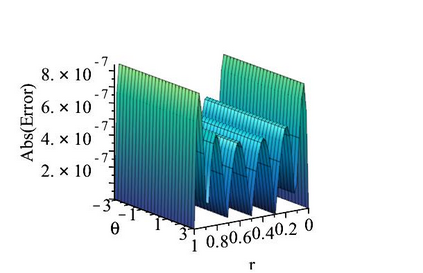
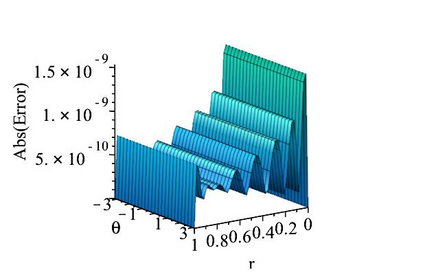
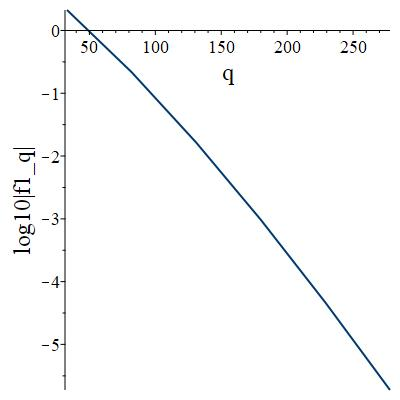
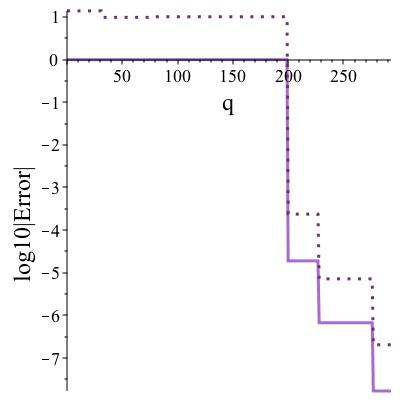
The subject of this paper is the design of efficient and stable spectral methods for time-dependent partial differential equations in unit balls. We commence by sketching the desired features of a spectral method, which is defined by a choice of an orthonormal basis acting in the spatial domain. We continue by considering in detail the choice of a $W$-function basis in a disc in $\mathbb{R}^2$. This is a nontrivial issue because of a clash between two objectives: skew symmetry of the differentiation matrix (which ensures inter alia that the method is stable) and the correct behaviour at the origin. We resolve it by representing the underlying space as an affine space and splitting the underlying functions. This is generalised to any dimension $d \geq 2$ in a natural manner and the paper is concluded with numerical examples that demonstrate how our choice of basis attains the best outcome out of a number of alternatives.
翻译:暂无翻译