A Universal Framework for Featurization of Atomistic Systems

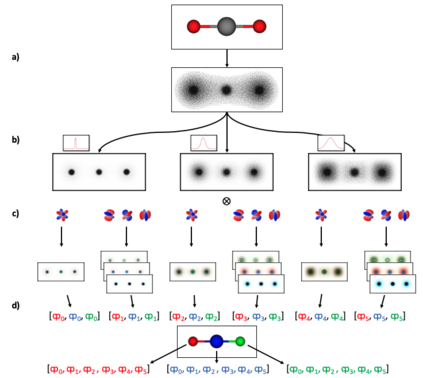
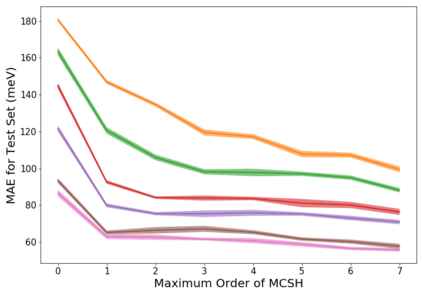
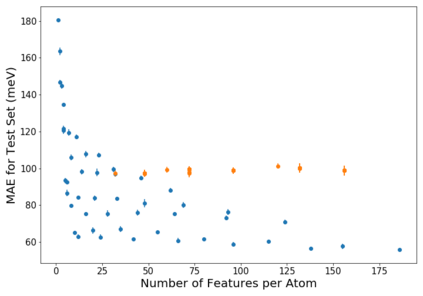
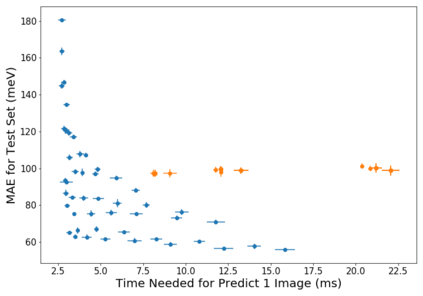
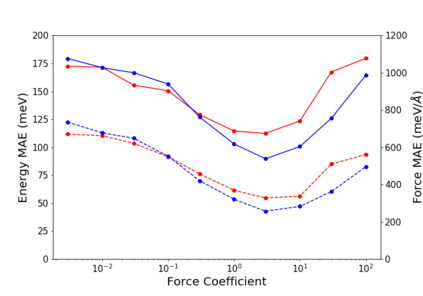
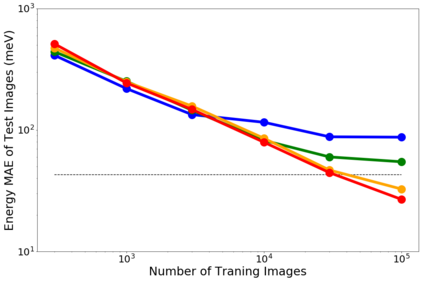
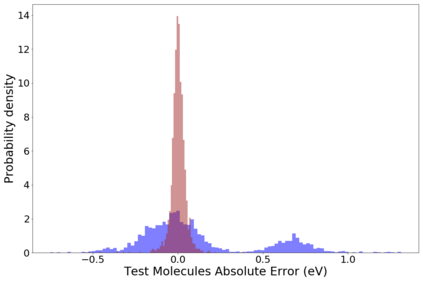
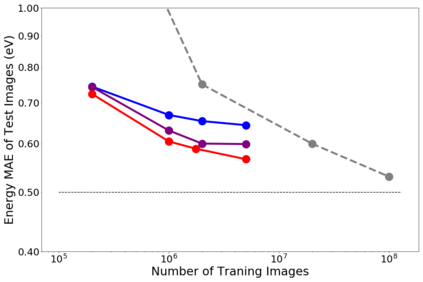
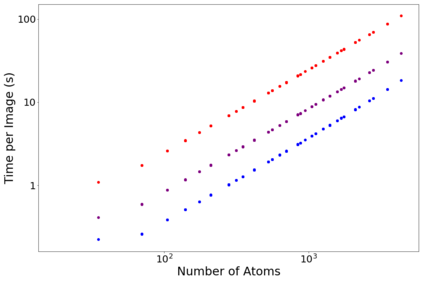
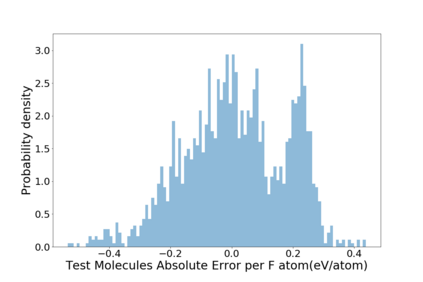
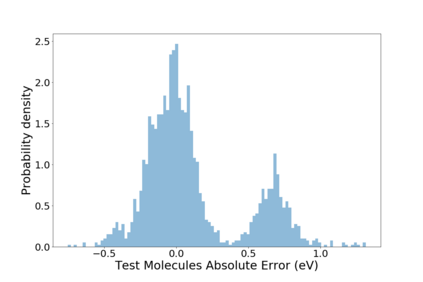
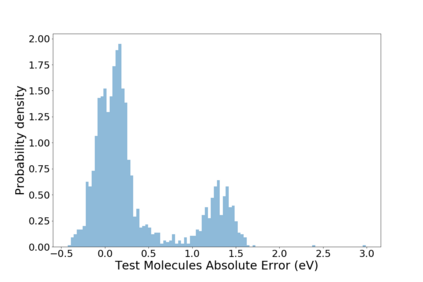
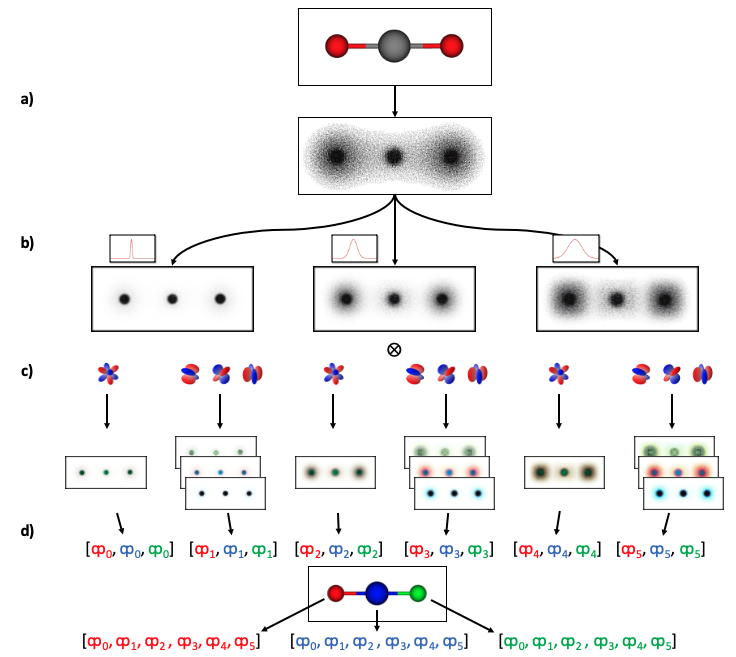
Molecular dynamics simulations are an invaluable tool in numerous scientific fields. However, the ubiquitous classical force fields cannot describe reactive systems, and quantum molecular dynamics are too computationally demanding to treat large systems or long timescales. Reactive force fields based on physics or machine learning can be used to bridge the gap in time and length scales, but these force fields require substantial effort to construct and are highly specific to a given chemical composition and application. A significant limitation of machine learning models is the use of element-specific features, leading to models that scale poorly with the number of elements. This work introduces the Gaussian multipole (GMP) featurization scheme that utilizes physically-relevant multipole expansions of the electron density around atoms to yield feature vectors that interpolate between element types and have a fixed dimension regardless of the number of elements present. We combine GMP with neural networks to directly compare it to the widely used Behler-Parinello symmetry functions for the MD17 dataset, revealing that it exhibits improved accuracy and computational efficiency. Further, we demonstrate that GMP-based models can achieve chemical accuracy for the QM9 dataset, and their accuracy remains reasonable even when extrapolating to new elements. Finally, we test GMP-based models for the Open Catalysis Project (OCP) dataset, revealing comparable performance to graph convolutional deep learning models. The results indicate that this featurization scheme fills a critical gap in the construction of efficient and transferable machine-learned force fields.