A Functional Operator for Model Uncertainty Quantification in the RKHS

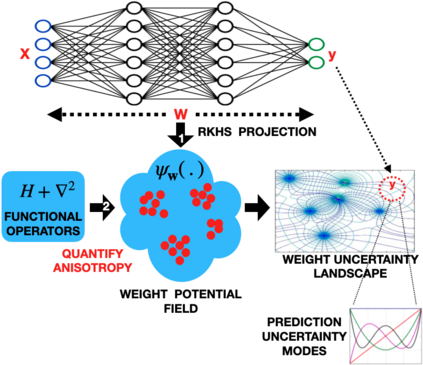
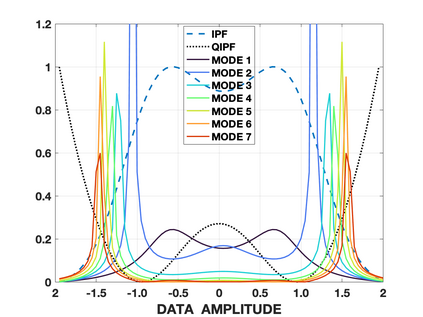
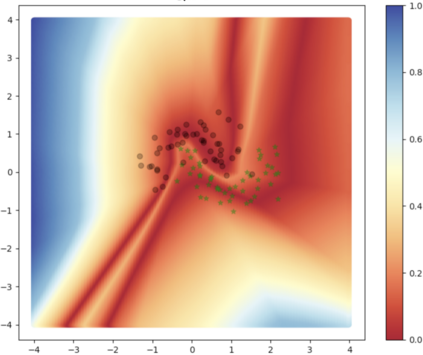
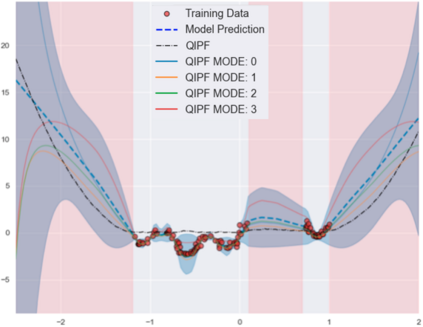
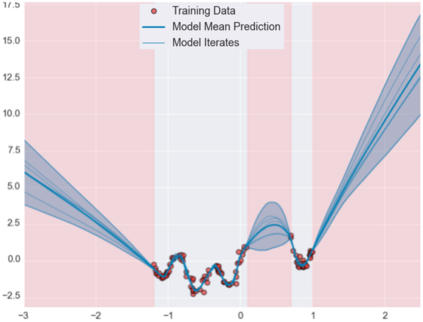
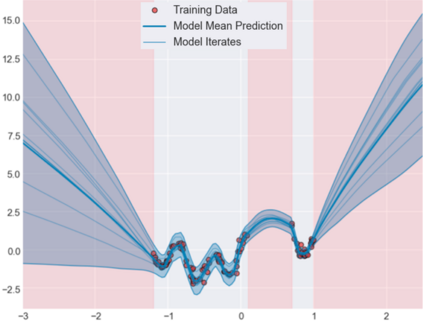
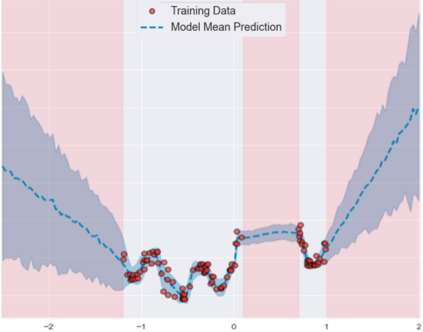
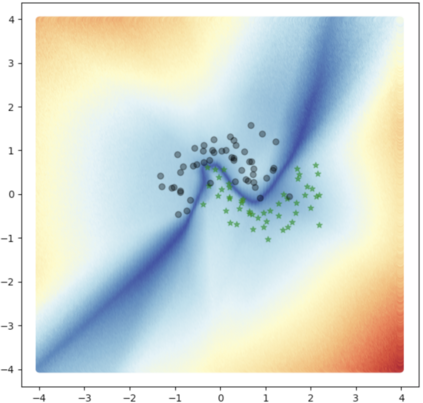
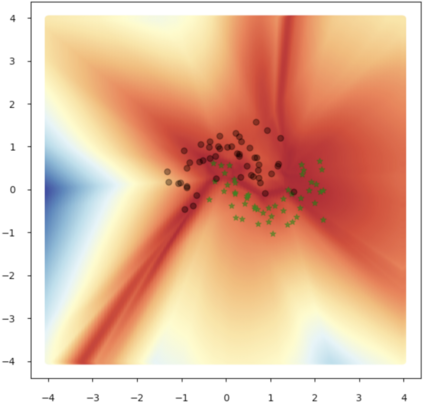
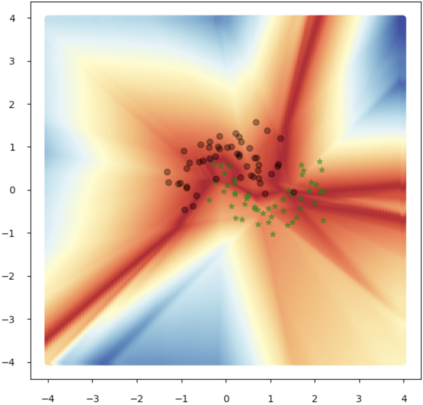
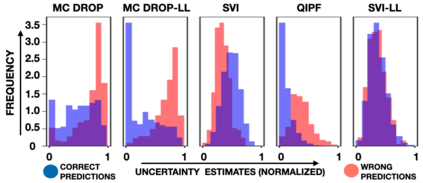
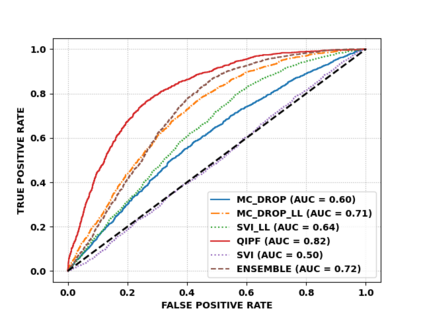
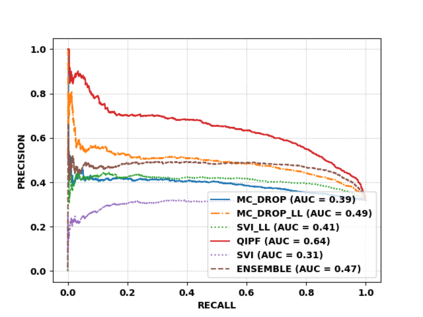
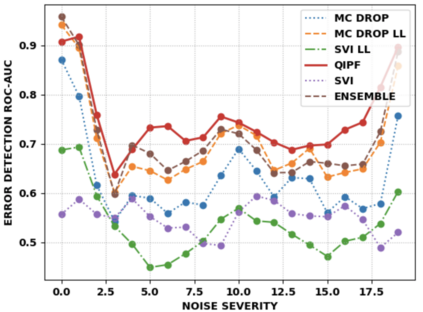
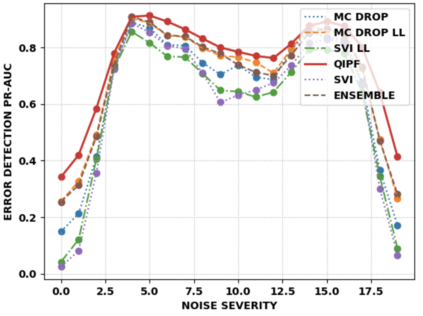
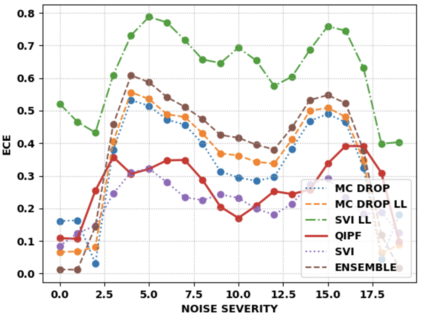
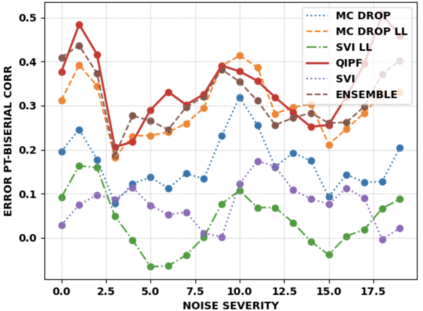
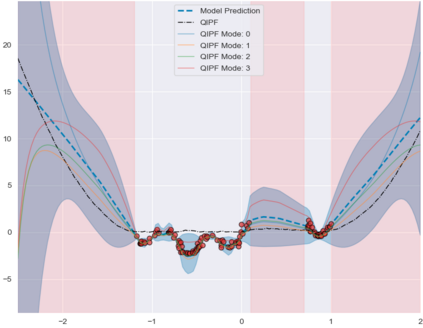
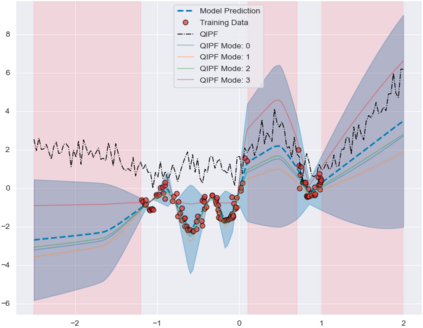
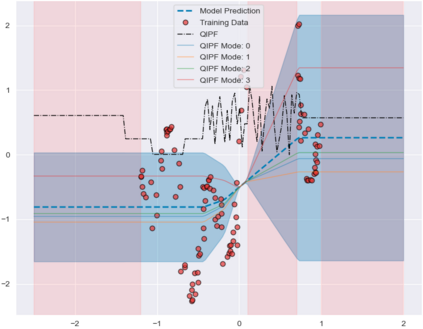
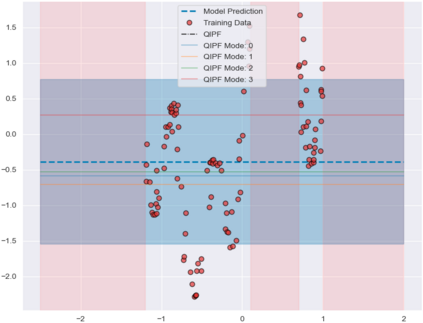
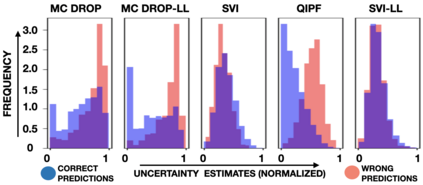
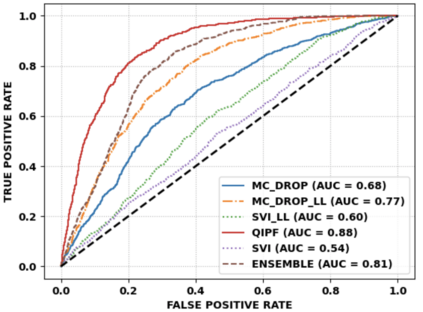
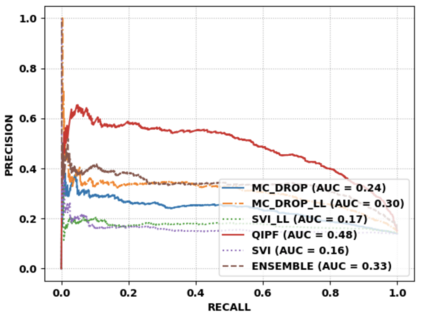
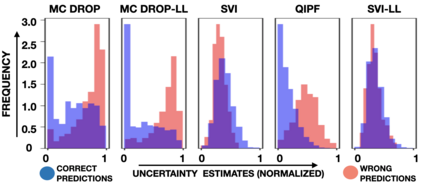
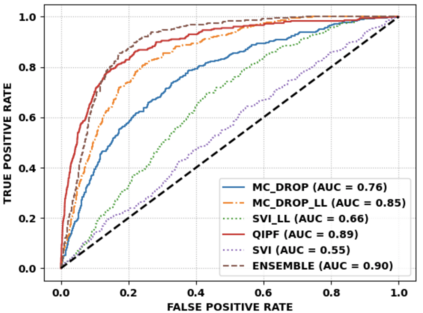
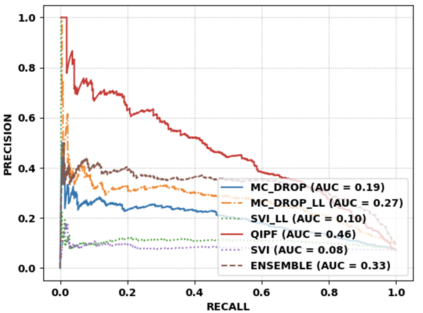
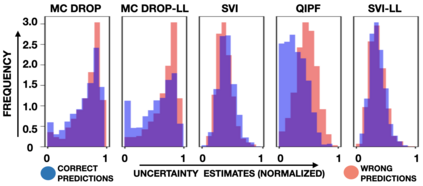
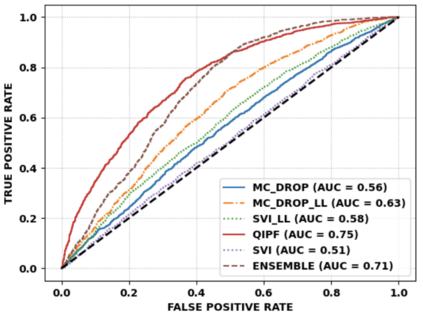
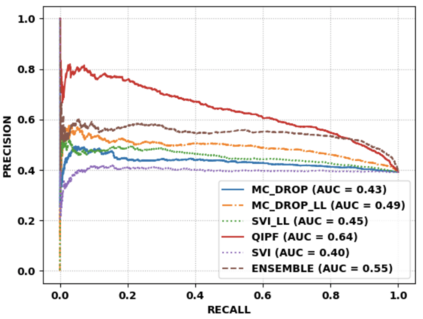
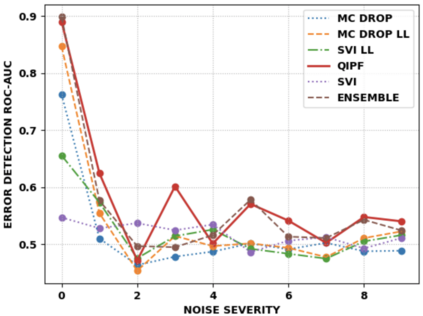
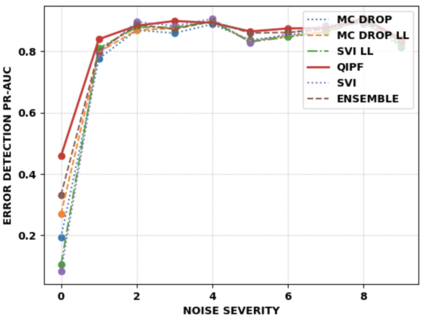
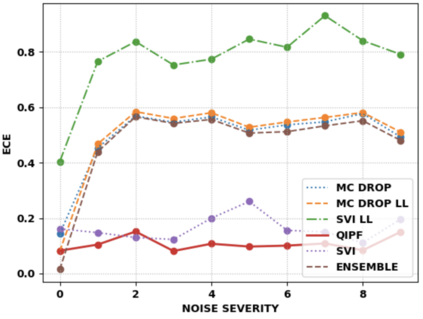
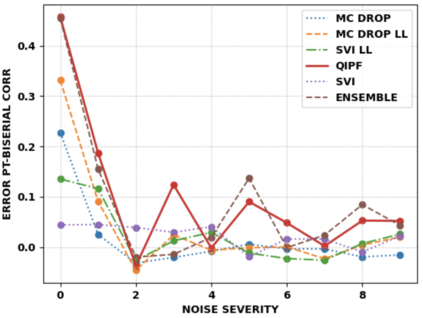
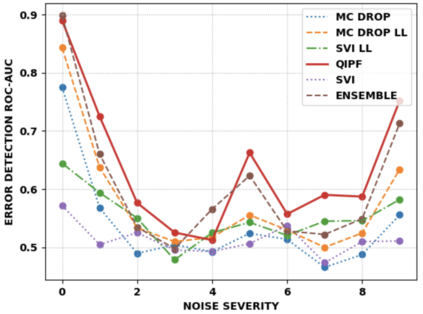
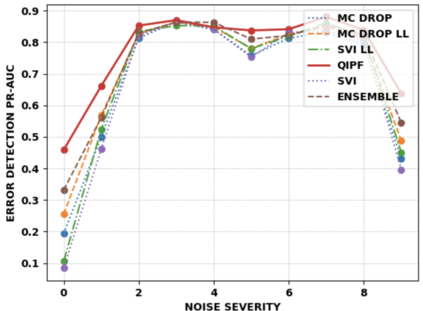
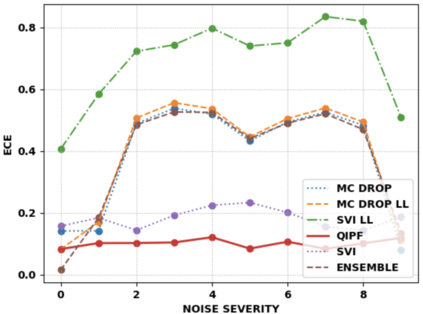
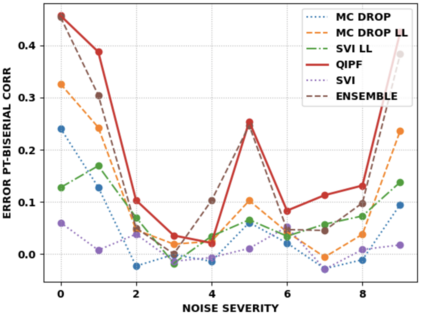
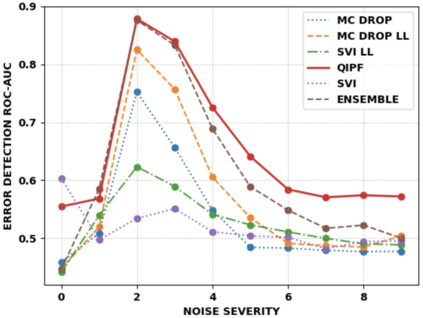
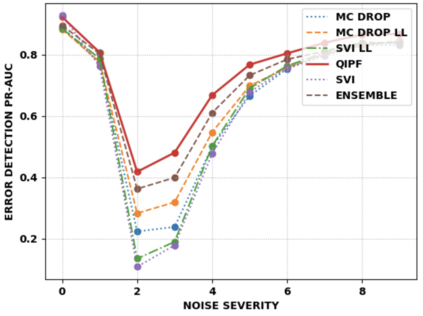
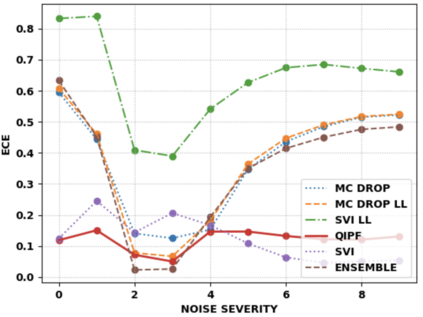
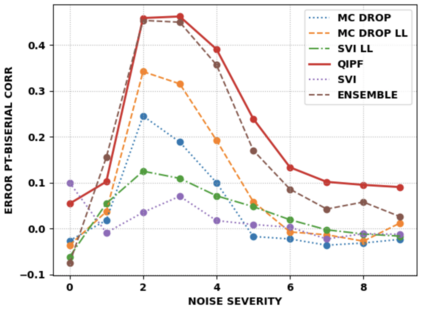
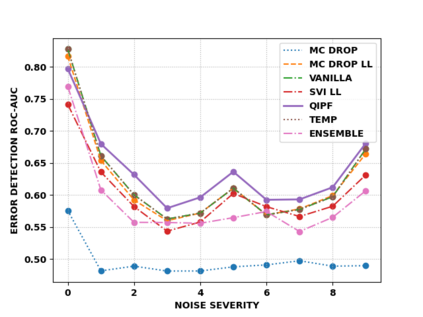
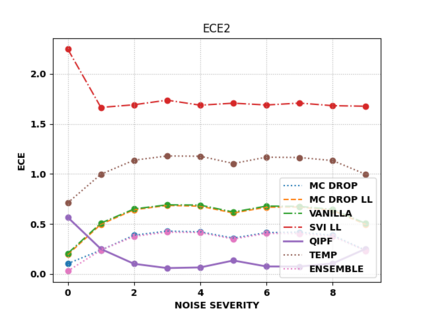
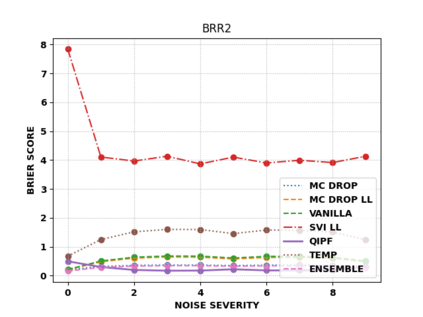
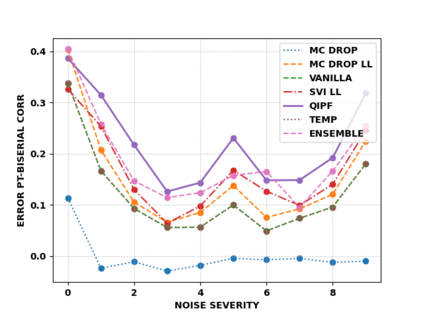
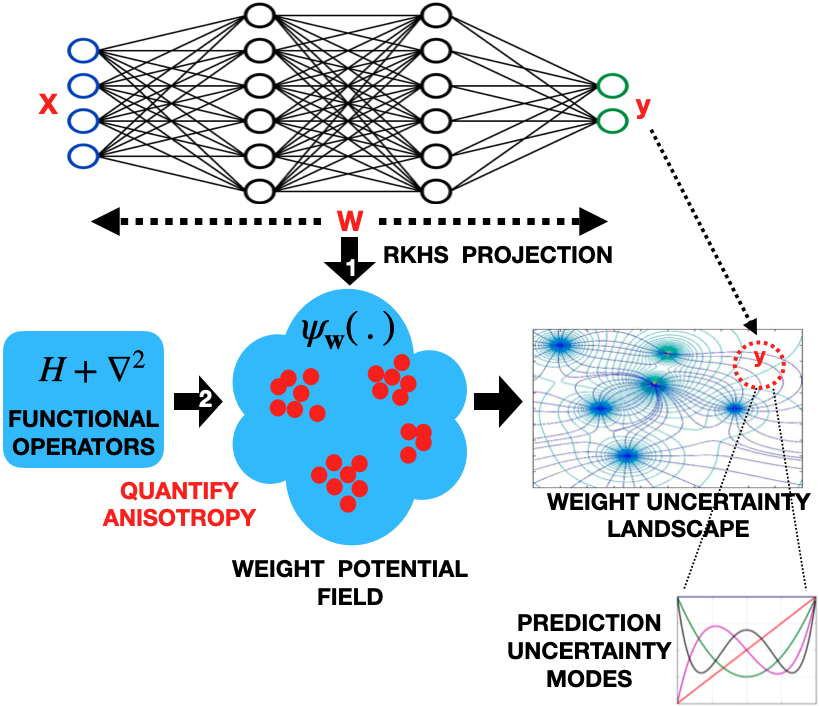
Accurate uncertainty quantification of model predictions is a crucial problem in machine learning. Existing Bayesian methods, relying on iterative procedures or Monte Carlo sampling, are computationally expensive to implement and often fail to capture the true posterior of a model, especially in high dimensional problems. This paper proposes a framework for single-shot predictive uncertainty quantification of a neural network that replaces the conventional Bayesian notion of weight probability density function (PDF) with a functional defined on the model weights in a reproducing kernel Hilbert space (RKHS). The resulting RKHS based analysis yields a potential field based interpretation of the model weight PDF and allows the definition of a functional operator, inspired by perturbation theory, that performs a moment decomposition of the model weight PDF to quantify uncertainty of the model predictions. The extracted moments from this approach automatically decompose the weight PDF around the local neighborhood of the specified model output and determine, with great sensitivity, the local heterogeneity and anisotropy of the weight PDF around a given model prediction output. Consequently, these functional moments provide much more precise and sharper estimates of model predictive uncertainty than the central stochastic moments characterized by Bayesian and ensemble methods. Experimental results demonstrate this by evaluating the error detection capability of the model uncertainty quantification methods on test data that has undergone a covariate shift away from the training PDF learned by the model. We find our proposed measure for uncertainty quantification to be significantly more precise and better calibrated than baseline methods on various benchmark datasets, while also being much faster to compute.