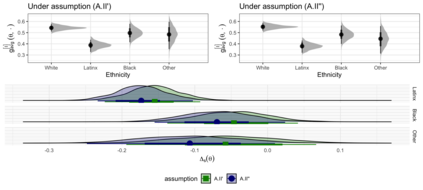
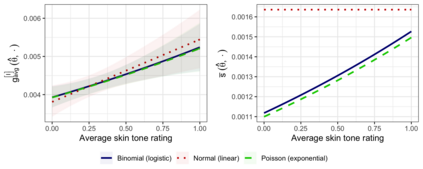
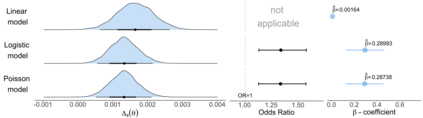
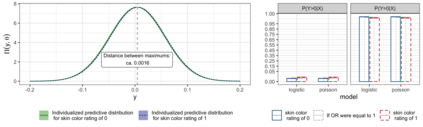
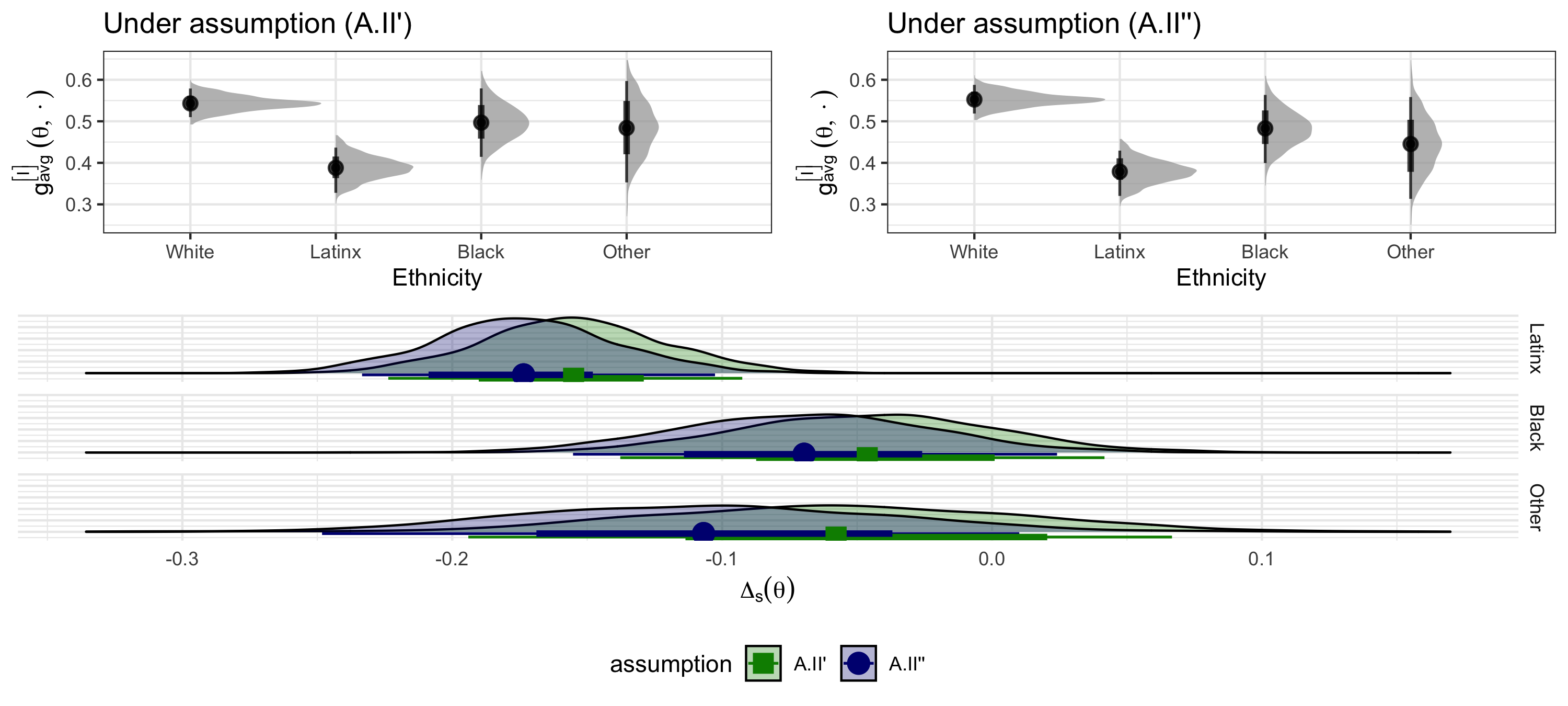
Effect size measures and visualization techniques aimed at maximizing the interpretability and comparability of results from statistical models have long been of great importance and are recently again receiving increased attention in the literature. However, since the methods proposed in this context originate from a wide variety of disciplines and are more often than not practically motivated, they lack a common theoretical framework and many quantities are narrowly or heuristically defined. In this work, we put forward a common mathematical setting for effect size measures and visualization techniques aimed at the results of parametric regression and define a formal framework for the consistent derivation of both existing and new variants of such quantities. Throughout the presented theory, we utilize probability measures to derive weighted means over areas of interest. While we take a Bayesian approach to quantifying uncertainty in order to derive consistent results for every defined quantity, all proposed methods apply to the results of both frequentist and Bayesian inference. We apply selected specifications derived from the proposed framework to data from a clinical trial and a multi-analyst study to illustrate its versatility and relevance.
翻译:旨在尽量扩大统计模型结果的可解释性和可比性的影响尺度和可视化技术长期以来一直非常重要,最近又在文献中受到越来越多的注意。然而,由于在这方面提议的方法来自广泛的学科,而且往往不是实际动机,因此缺乏共同的理论框架,许多数量是狭义或粗略界定的。在这项工作中,我们提出了一个关于影响尺度测量和可视化技术的共同数学设置,目的是得出参数回归的结果,并为统一得出此类数量的现有和新的变异提供了一个正式框架。我们在整个理论中,利用概率计量方法,在利益领域上得出加权手段。我们采取贝耶斯方法量化不确定性,以取得每个确定数量一致的结果,而所有拟议方法都适用于常见和拜耶斯人推论的结果。我们从拟议框架中选定的规格用于临床试验和多分析研究中的数据,以说明其多功能性和相关性。