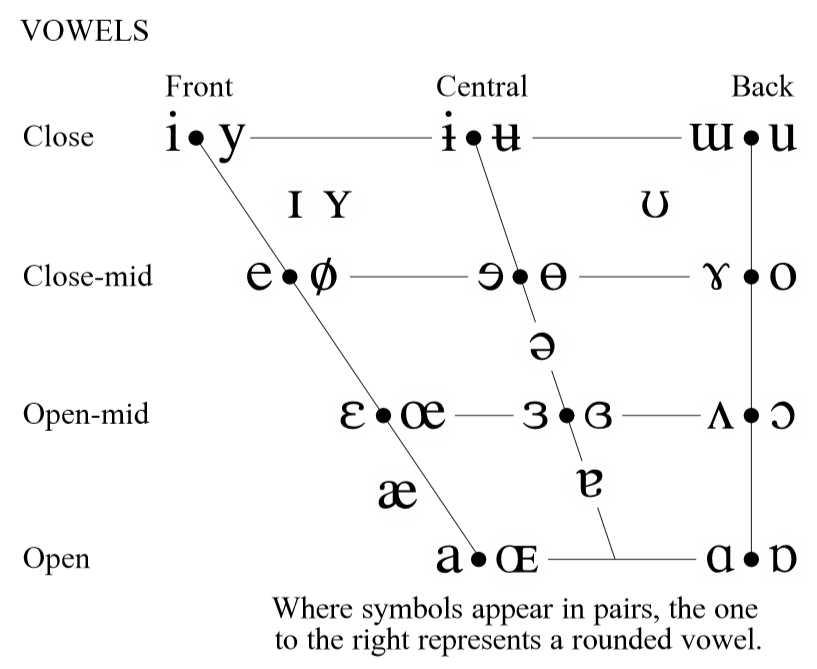
Vast literature on experimental design extends from Fisher and Snedecor to the modern day. When data lies beyond the assumption of univariate normality, nonparametric methods including rank based statistics and permutation tests are enlisted. The permutation test is a versatile exact nonparametric significance test that requires drastically fewer assumptions than similar parametric tests. The main downfall of the permutation test is high computational cost making this approach laborious for complex data and sophisticated experimental designs and completely infeasible in any application requiring speedy results such as high throughput streaming data. We rectify this problem through application of concentration inequalities and thus propose a computation free permutation test -- i.e. a permutation-less permutation test. This general framework is applied to multivariate, matrix-valued, and functional data. We improve these concentration bounds via a novel incomplete beta transform. We extend our theory from 2-sample to $k$-sample testing through the use of weakly dependent Rademacher chaoses and modified decoupling inequalities. We test this methodology on classic functional data sets including the Berkeley growth curves and the phoneme dataset. We further consider analysis of spoken vowel sound under two experimental designs: the Latin square and the randomized block design.
翻译:实验设计的大量文献从Fisher 和 Snecorsor 延伸到现代。 当数据超出单向正常状态假设范围时, 需要使用非参数方法, 包括按级统计和变异测试。 变异测试是一种多功能的、 非参数意义测试, 需要的假设比类似的参数测试少得多。 变异测试的主要下降是高计算成本, 这使得这一方法在复杂数据和尖端实验设计方面耗费大量精力, 在任何需要快速结果的应用程序中完全不可行, 如高吞吐流数据。 我们通过应用浓度不平等来纠正这一问题, 从而提出一个计算自由变异测试 -- -- 即不按级统计和变异测试。 这个总框架适用于多种变异性、 矩阵估值和功能性数据。 我们通过新的不完全的贝塔变来改进这些浓缩的界限。 我们通过使用依赖性不强的Rademacher 混和经修改的分解不平等性数据来扩大我们的理论范围。 我们进一步测试这一方法, 包括伯克利增长曲线 和 语音设计 。