An unfitted radial basis function generated finite difference method applied to thoracic diaphragm simulations

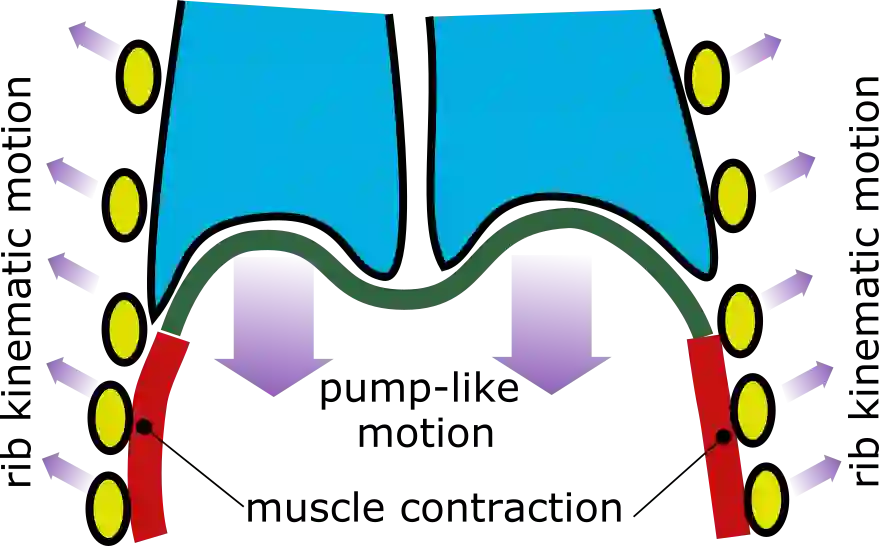
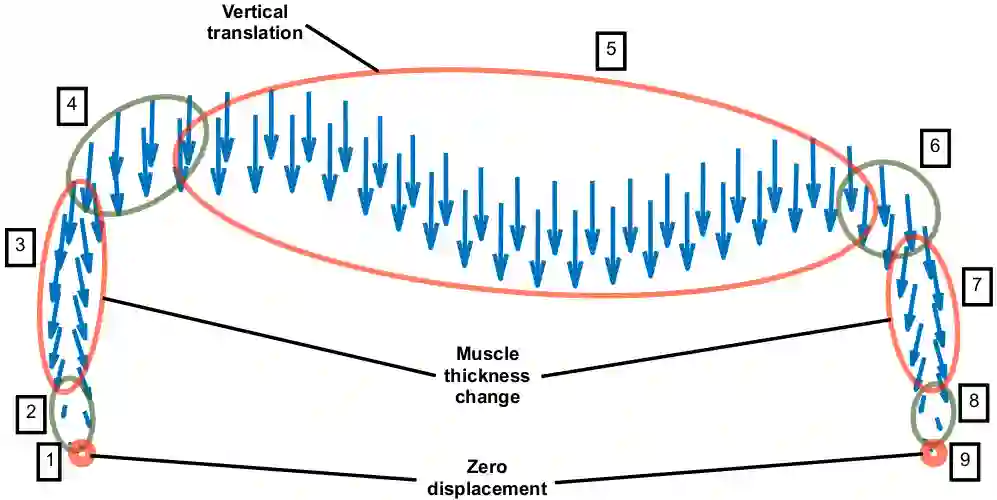
The thoracic diaphragm is the muscle that drives the respiratory cycle of a human being. Using a system of partial differential equations (PDEs) that models linear elasticity we compute displacements and stresses in a two-dimensional cross section of the diaphragm in its contracted state. The boundary data consists of a mix of displacement and traction conditions. If these are imposed as they are, and the conditions are not compatible, this leads to reduced smoothness of the solution. Therefore, the boundary data is first smoothed using the least-squares radial basis function generated finite difference (RBF-FD) framework. Then the boundary conditions are reformulated as a Robin boundary condition with smooth coefficients. The same framework is also used to approximate the boundary curve of the diaphragm cross section based on data obtained from a slice of a computed tomography (CT) scan. To solve the PDE we employ the unfitted least-squares RBF-FD method. This makes it easier to handle the geometry of the diaphragm, which is thin and non-convex. We show numerically that our solution converges with high-order towards a finite element solution evaluated on a fine grid. Through this simplified numerical model we also gain an insight into the challenges associated with the diaphragm geometry and the boundary conditions before approaching a more complex three-dimensional model.