Switched Systems as Hybrid Programs

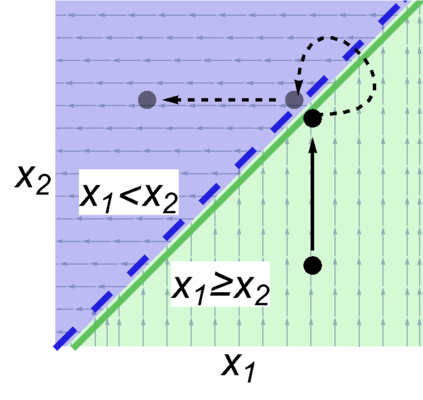
Real world systems of interest often feature interactions between discrete and continuous dynamics. Various hybrid system formalisms have been used to model and analyse this combination of dynamics, ranging from mathematical descriptions, e.g., using impulsive differential equations and switching, to automata-theoretic and language-based approaches. This paper bridges two such formalisms by showing how various classes of switched systems can be modeled using the language of hybrid programs from differential dynamic logic (dL). The resulting models enable the formal specification and verification of switched systems using dL and its existing deductive verification tools such as KeYmaera X. Switched systems also provide a natural avenue for the generalization of dL's deductive proof theory for differential equations. The completeness results for switched system invariants proved in this paper enable effective safety verification of those systems in dL.