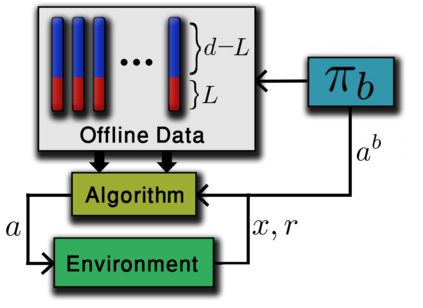
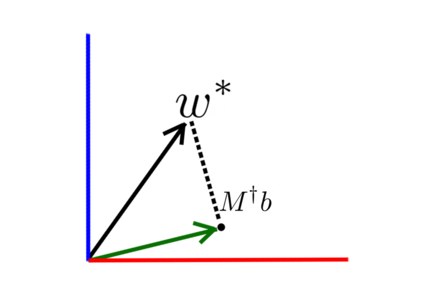
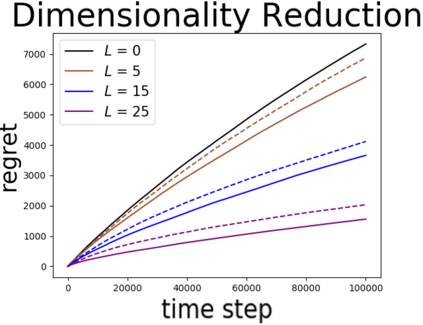
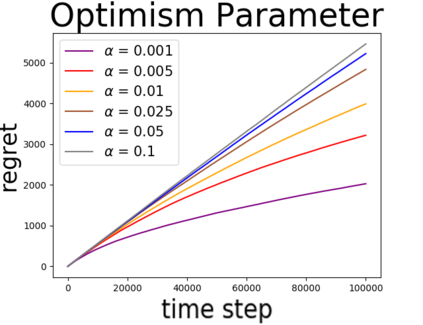
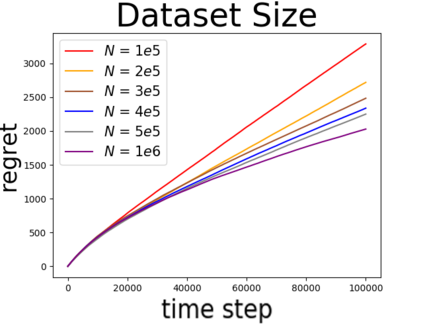
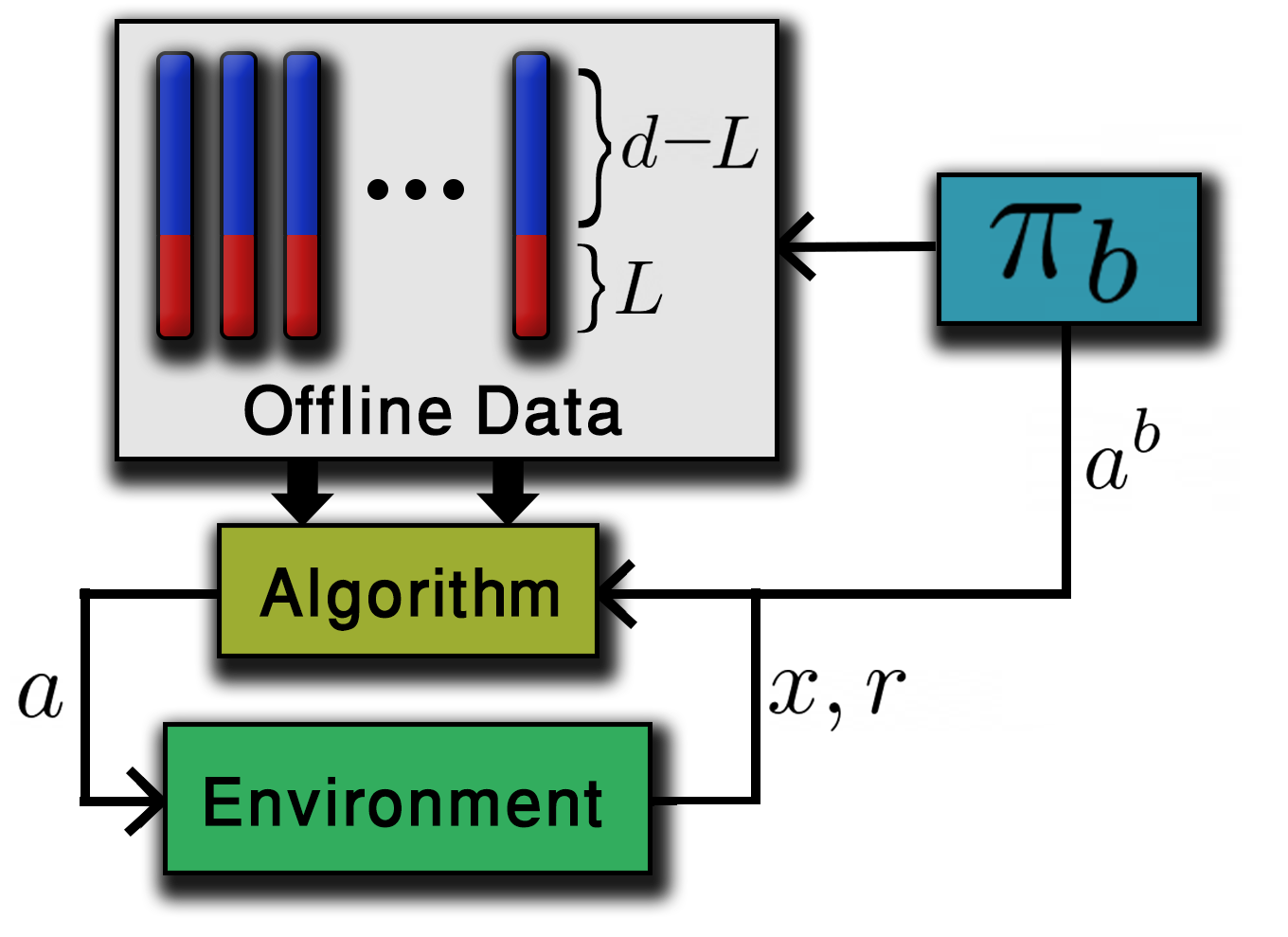
We study linear contextual bandits with access to a large, confounded, offline dataset that was sampled from some fixed policy. We show that this problem is closely related to a variant of the bandit problem with side information. We construct a linear bandit algorithm that takes advantage of the projected information, and prove regret bounds. Our results demonstrate the ability to take advantage of confounded offline data. Particularly, we prove regret bounds that improve current bounds by a factor related to the visible dimensionality of the contexts in the data. Our results indicate that confounded offline data can significantly improve online learning algorithms. Finally, we demonstrate various characteristics of our approach through synthetic simulations.
翻译:我们研究线性背景强盗,可以访问从某种固定政策中抽样的大型、令人困惑的离线数据集。我们发现,这个问题与随身资料的盗匪问题的变种密切相关。我们构建了一个线性土匪算法,利用预测的信息,并证明有悔意界限。我们的结果表明,有能力利用无根据的离线数据。特别是,我们证明,由于数据上下文的可见维度相关因素而改善当前界限的令人遗憾的界限。我们的结果表明,混结的离线性数据能够大大改进在线学习算法。最后,我们通过合成模拟展示了我们方法的各种特征。