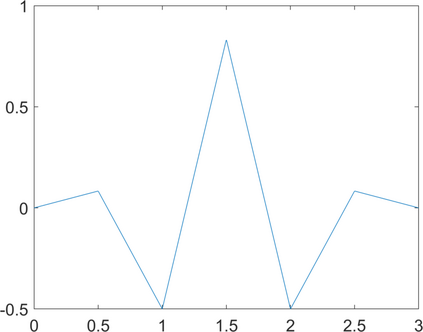
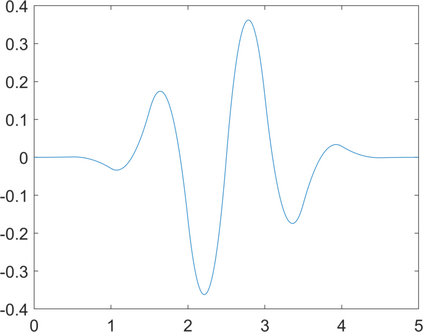
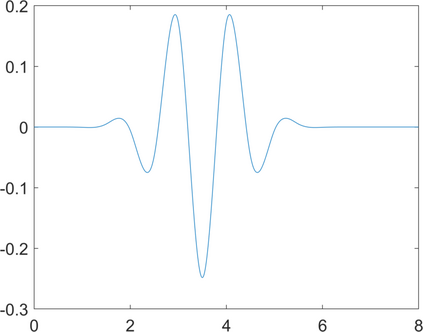
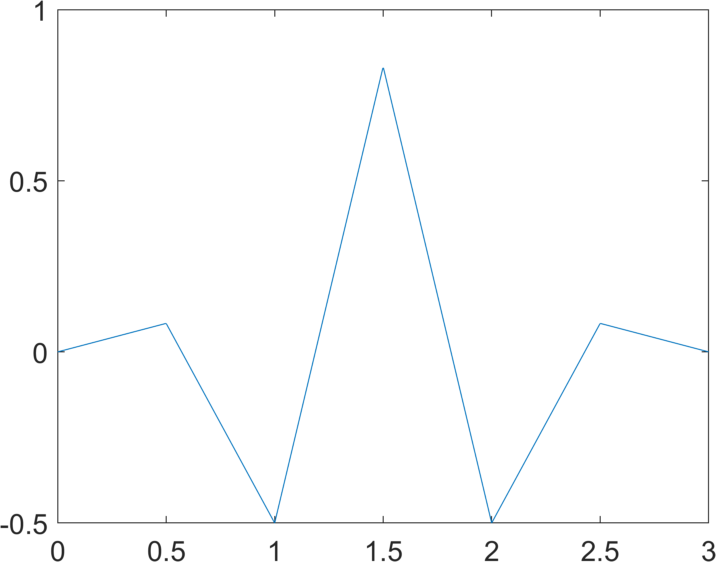
We use hyperbolic wavelet regression for the fast reconstruction of high-dimensional functions having only low dimensional variable interactions. Compactly supported periodic Chui-Wang wavelets are used for the tensorized hyperbolic wavelet basis. In a first step we give a self-contained characterization of tensor product Sobolev-Besov spaces on the $d$-torus with arbitrary smoothness in terms of the decay of such wavelet coefficients. In the second part we perform and analyze scattered-data approximation using a hyperbolic cross type truncation of the basis expansion for the associated least squares method. The corresponding system matrix is sparse due to the compact support of the wavelets, which leads to a significant acceleration of the matrix vector multiplication. In case of i.i.d. samples we can even bound the approximation error with high probability by loosing only $\log$-terms that do not depend on $d$ compared to the best approximation. In addition, if the function has low effective dimension (i.e. only interactions of few variables), we qualitatively determine the variable interactions and omit ANOVA terms with low variance in a second step in order to increase the accuracy. This allows us to suggest an adapted model for the approximation. Numerical results show the efficiency of the proposed method.
翻译:我们使用双曲线波子回归法快速重建仅具有低维变量相互作用的高维函数。 压缩支持的周期清- Wang波子波子用于加压双曲波子基础。 第一步, 我们给 $d- turus 空间上高压产品 Sobolev- Besov 空间进行自足的定性, 在这种波子系数的衰减方面, 任意平稳地将美元乘以美元; 在第二部分, 我们使用相关最小方块法基础扩展的双曲线跨类型轨迹执行并分析分散的数据近似值。 由于波子的紧凑支持, 相应的系统矩阵是稀疏的, 从而导致矩阵矢量的大幅加速倍增。 在 i. d. 样本中, 我们甚至可以将近似误差以很高的概率捆绑绑定, 仅使用美元=log$- terms, 与最佳近似值相比不依赖美元。 此外, 如果函数的低有效维度( 即只有少数变量的交互作用), 我们定性地确定变量的交互作用, 并忽略了相应的系统矩阵矩阵矩阵矩阵矩阵矩阵矩阵矩阵矩阵, 以显示低的精确度。