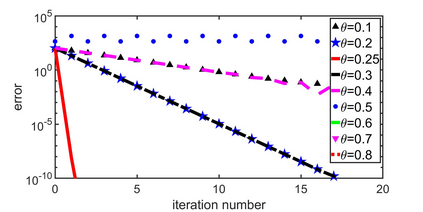
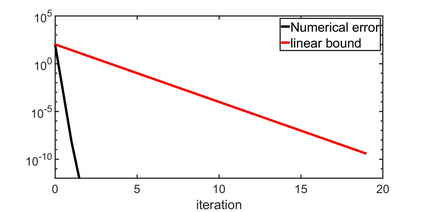
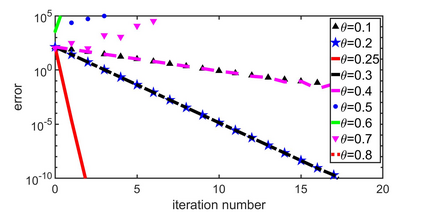
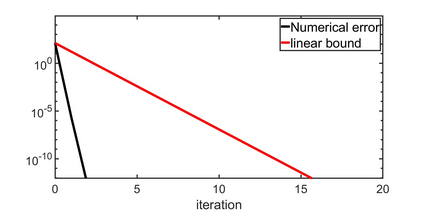
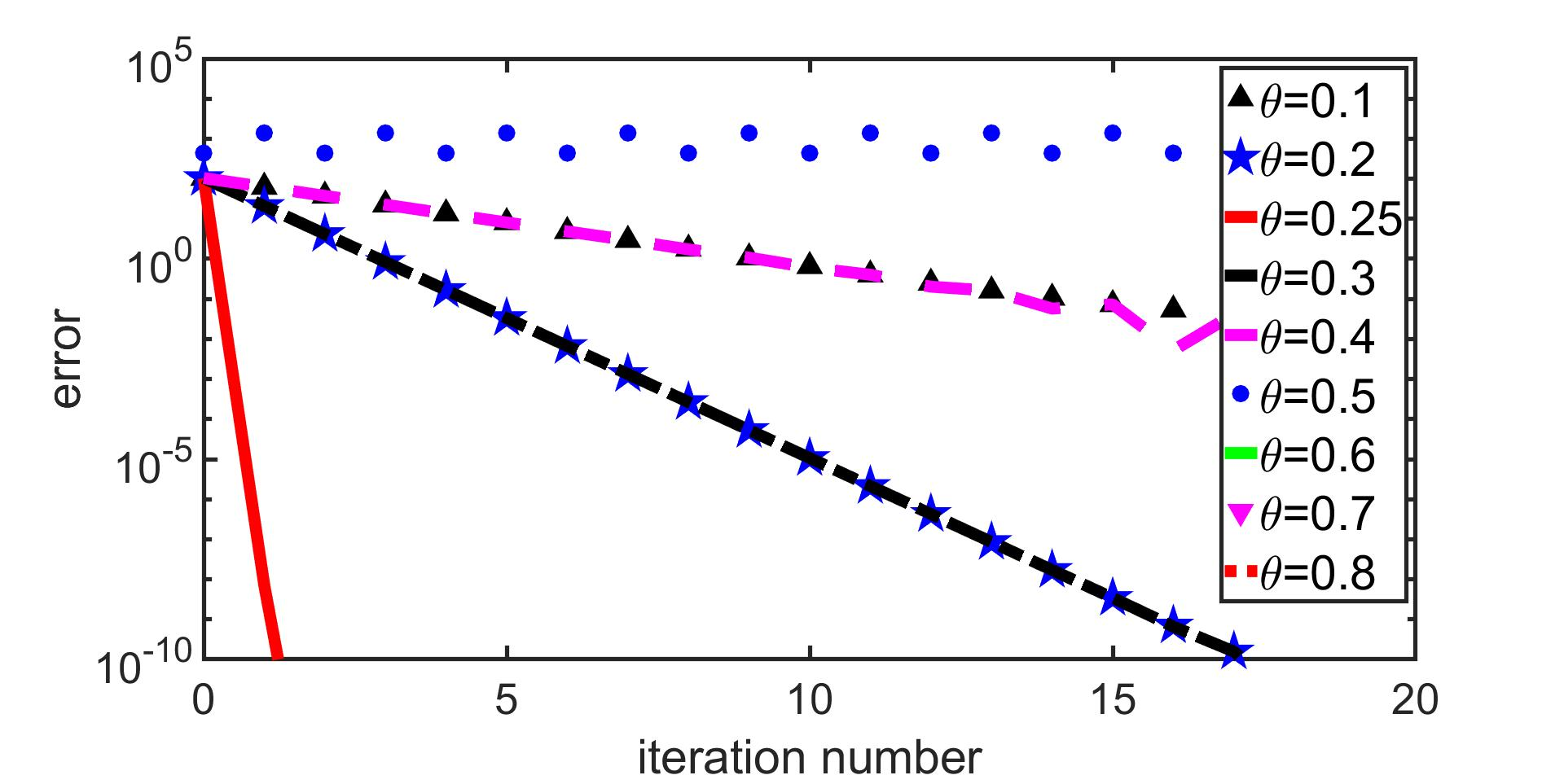
In this paper, we analyze a substructuring type algorithm for the Cahn-Hilliard (CH) equation. Being a nonlinear equation, it is of great importance to develop efficient numerical schemes for investigating the solution behaviour of the CH equation. We present the formulation of Neumann-Neumann (NN) method applied to the CH equation and investigate the convergence behaviour of the same in one and two spatial dimension for two subdomains. We illustrate the theoretical results by providing numerical example.
翻译:在本文中,我们分析了Cahn-Hilliard(CH)等式的亚结构算法类型。作为一个非线性方程式,为调查CH等式的解决方案行为制定有效的数字计划非常重要。我们介绍了适用于CH等式的Neumann-Neumann(NN)方法的提法,并调查了两个子域在一两个空间层面的相同趋同行为。我们通过提供数字示例来说明理论结果。
相关内容
专知会员服务
36+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2021年9月8日
Arxiv
0+阅读 · 2021年9月8日
Arxiv
0+阅读 · 2021年9月8日
Arxiv
0+阅读 · 2021年9月7日
Arxiv
0+阅读 · 2021年9月7日