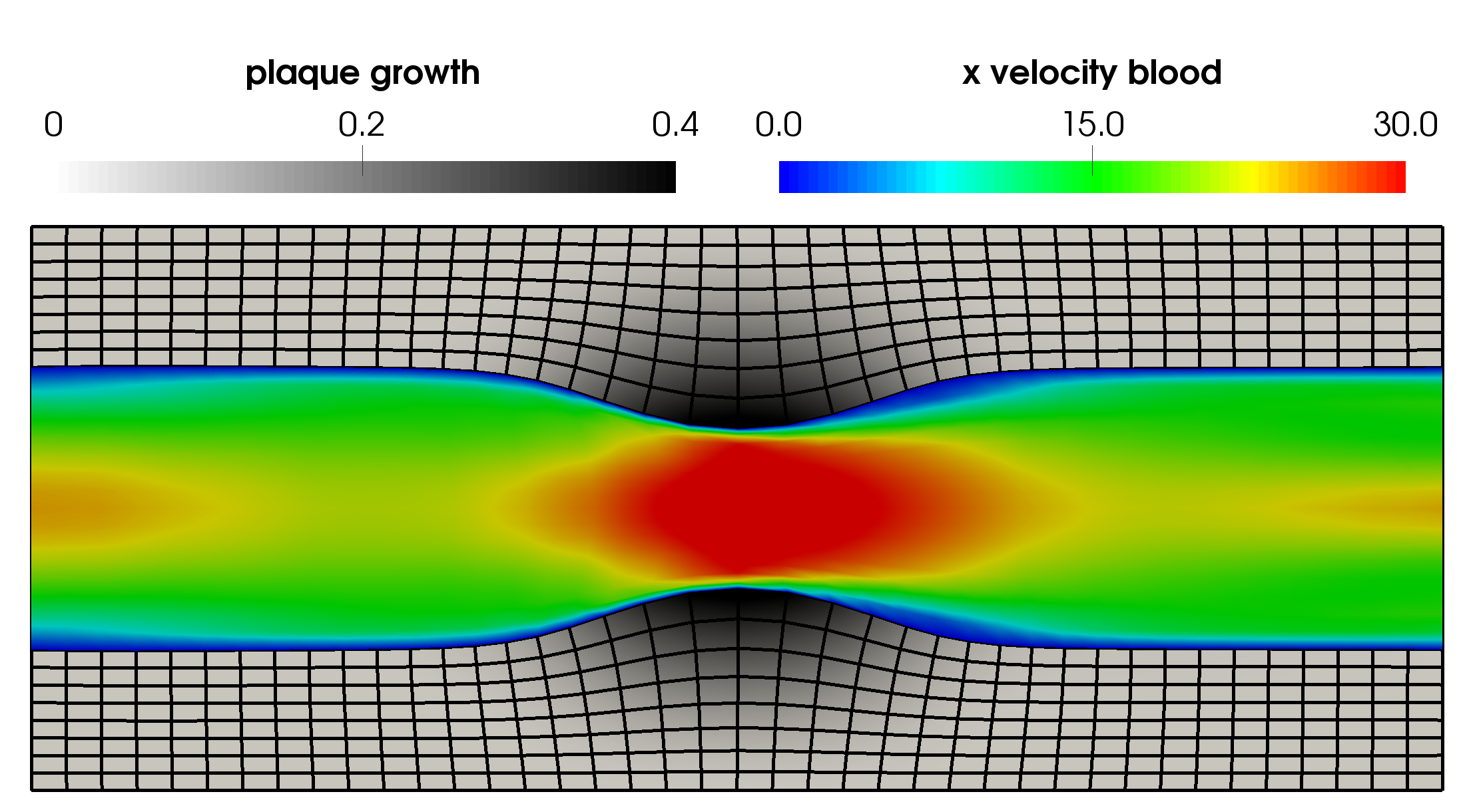
In order to make the numerical simulation of atherosclerotic plaque growth feasible, a temporal homogenization approach is employed. The resulting macro-scale problem for the plaque growth can be further accelerated by using parallel time integration schemes, such as the parareal algorithm. However, the parallel scalability is dominated by the computational cost of the coarse propagator. Therefore, in this paper, an interpolation-based coarse propagator, which uses growth values from previously computed micro-scale problems, is introduced. For a simple model problem, it is shown that this approach reduces both the computational work for a single parareal iteration as well as the required number of parareal iterations.
翻译:为了便于对无神论感应广场增长进行数字模拟,采用了一种时间同质化方法,通过使用平行时间集成办法,例如准正数算法,可以进一步加速产生对白板增长的宏观规模问题,但是,平行的可缩放性主要取决于粗肿传播器的计算成本。因此,本文件采用了一种基于内插的粗发传播器,它使用以前计算过的微观规模问题的增长值。对于一个简单的模型问题,它表明这种方法既减少了单次真实变异的计算工作,又减少了所要求的假变异数。