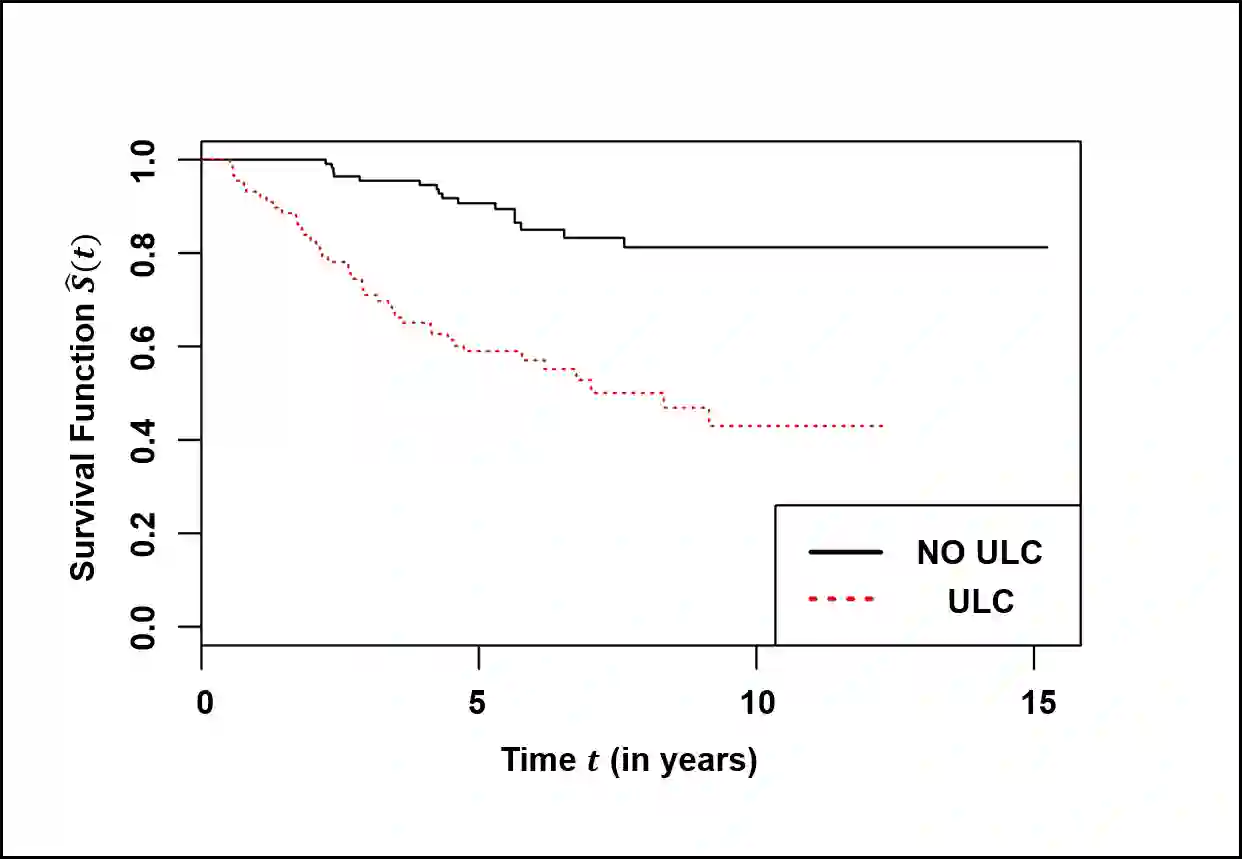
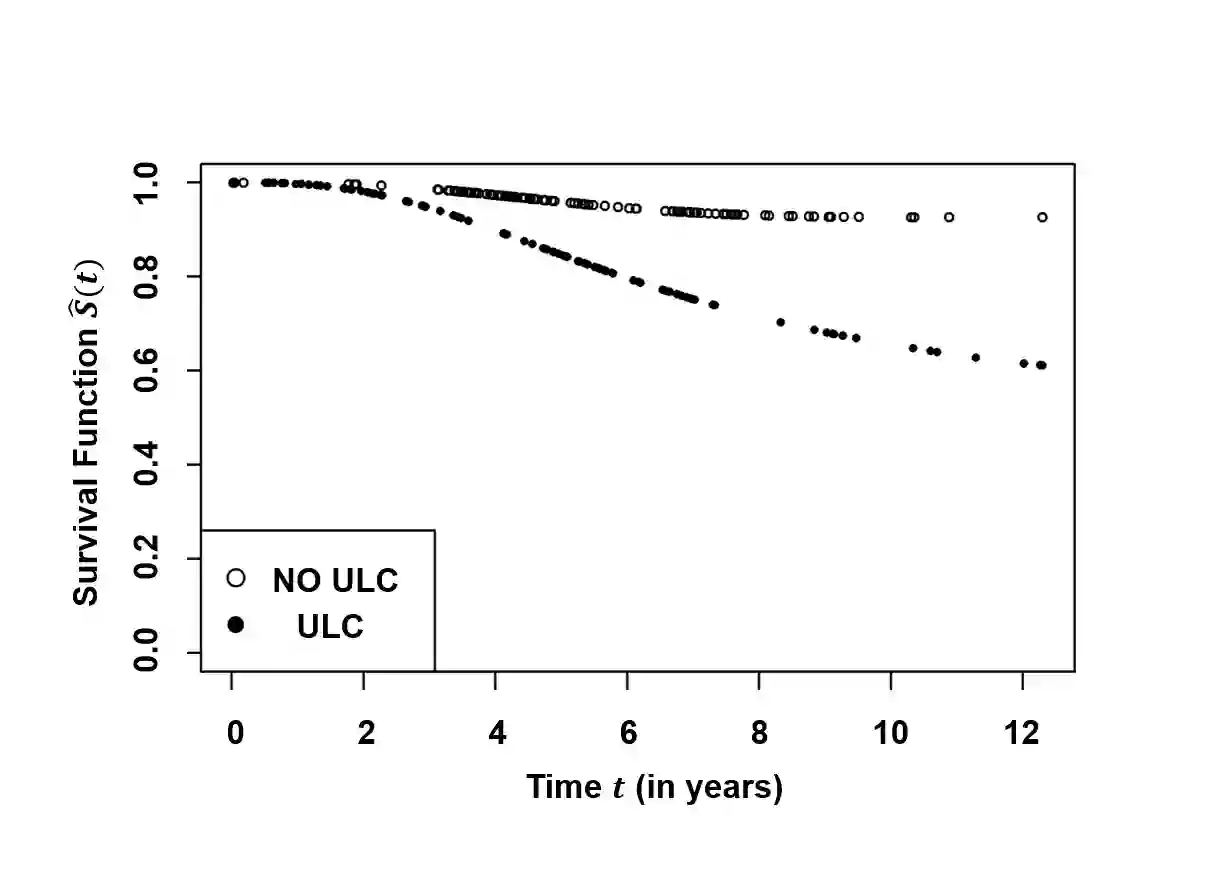
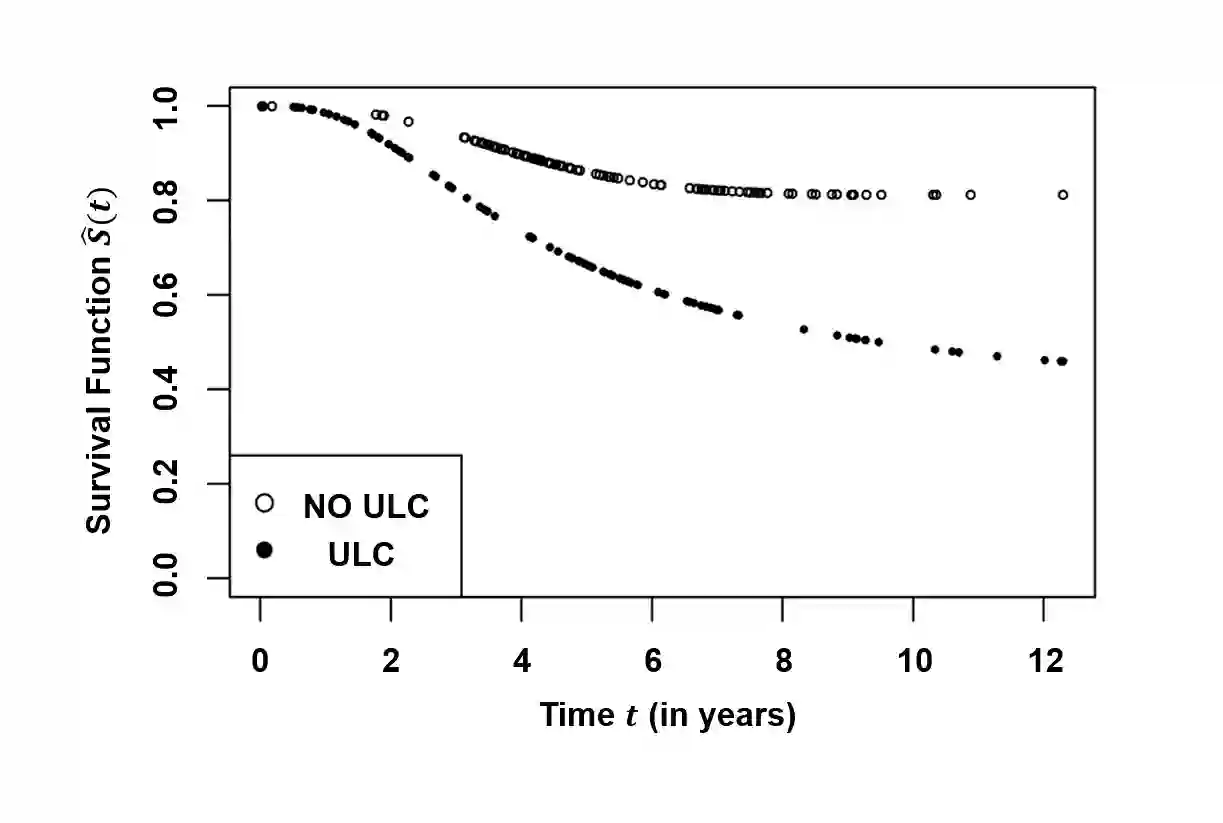
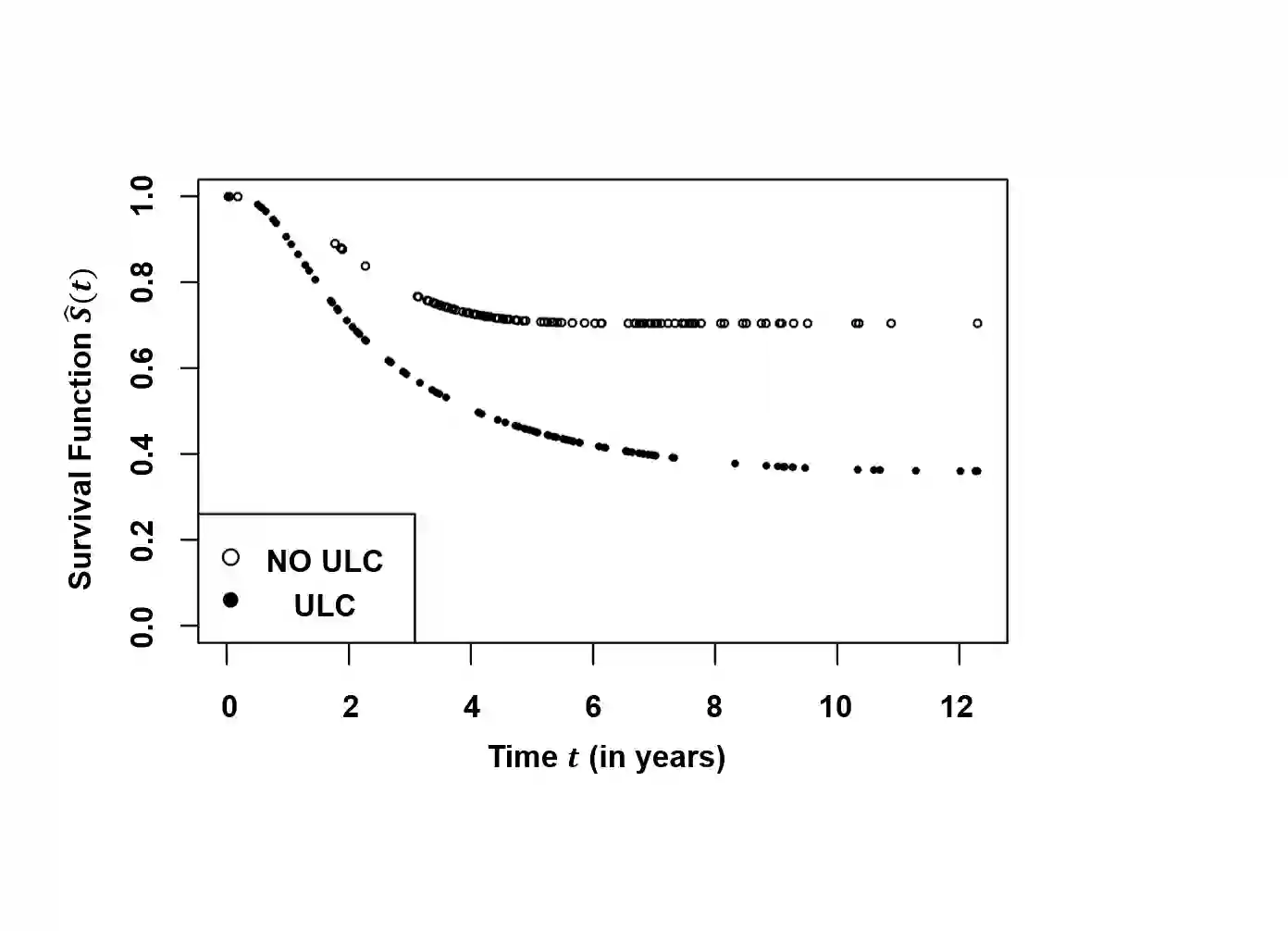
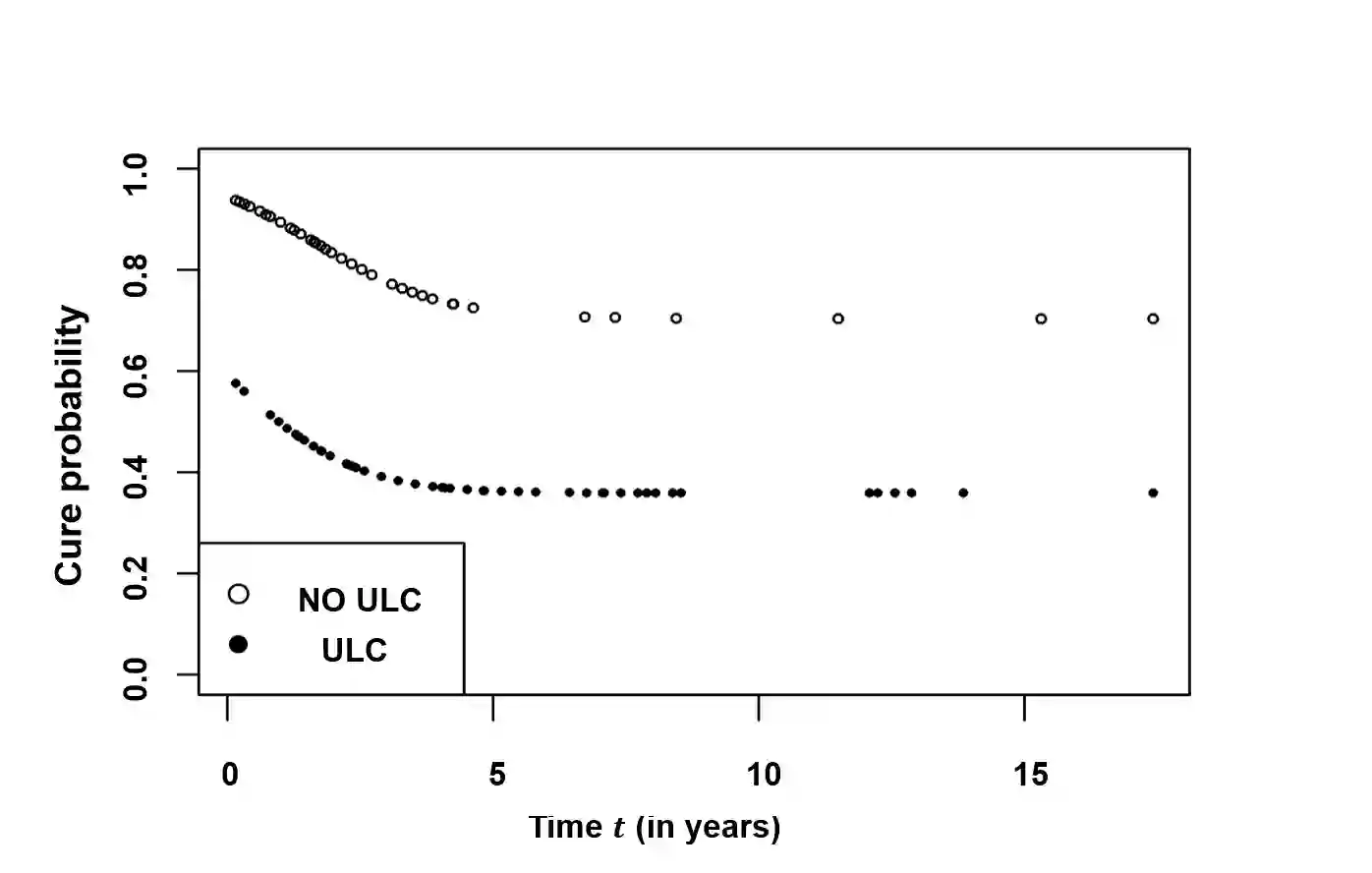
In survival analysis, cure models have gained much importance due to rapid advancements in medical sciences. More recently, a subset of cure models, called destructive cure models, have been studied extensively under competing risks scenario wherein initial competing risks undergo a destructive process, such as under a chemotherapy. In this article, we study destructive cure models by assuming a flexible weighted Poisson distribution (exponentially weighted Poisson, length biased Poisson and negative binomial distributions) for the initial number of competing causes and with lifetimes of the susceptible individuals following proportional hazards. The expectation-maximization (EM) algorithm and profile likelihood approach are made use of for estimating the model parameters. An extensive simulation study is carried out under various parameter settings to examine the properties of the models, and the accuracy and robustness of the proposed estimation technique. Effects of model misspecification on the parameter estimates are also discussed in detail. Finally, for the illustration of the proposed methodology, a real-life cutaneous melanoma data set is analyzed.
翻译:在生存分析中,由于医学的迅速进步,治愈模型的重要性已大增;最近,在相互竞争的风险假设下,广泛研究了一系列治疗模型,称为破坏性治疗模型,在相互竞争的风险假设下,最初相互竞争的风险经历破坏性过程,例如在化疗下;在本篇文章中,我们研究破坏性治疗模型,假设对相竞争原因的最初数量和受感染者在相称危害之后的寿命,采用灵活的加权Poisson分布(Excential graphy Poisson,长度偏差Poisson和负二进制分布),对参数估计的影响进行灵活加权加权分析;在估计模型参数参数时,利用预期-最大化算法和剖析可能性方法进行估计;在各种参数设置下进行广泛的模拟研究,审查模型的特性,以及拟议的估计技术的准确性和稳健性;还详细讨论了模型对参数估计的偏差影响。最后,为了说明拟议方法,分析了真实生命切度的黑皮瘤数据集。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem