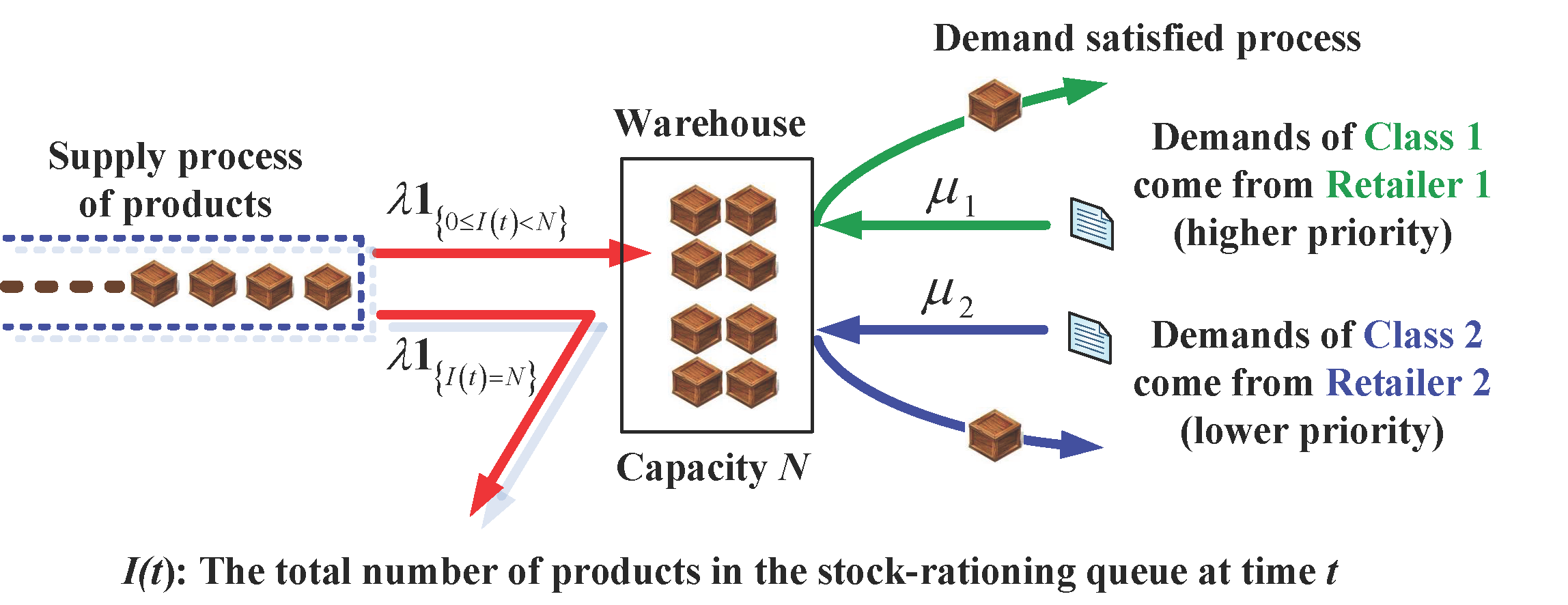
In this paper, we study a stock-rationing queue with two demand classes by means of the sensitivity-based optimization, and develop a complete algebraic solution to the optimal dynamic rationing policy. We show that the optimal dynamic rationing policy must be of transformational threshold type. Based on this finding, we can refine three sufficient conditions under each of which the optimal dynamic rationing policy is of threshold type (i.e., critical rationing level). To do this, we use the performance difference equation to characterize the monotonicity and optimality of the long-run average profit of this system, and thus establish some new structural properties of the optimal dynamic rationing policy by observing any given reference policy. Finally, we use numerical experiments to demonstrate our theoretical results of the optimal dynamic rationing policy. We believe that the methodology and results developed in this paper can shed light on the study of stock-rationing queues and open a series of potentially promising research.
翻译:在本文中,我们通过基于敏感度的优化,研究以两个需求类别排列的库存分级队列,并为最佳动态配给政策开发一个完整的代数解决方案。我们表明,最佳动态配给政策必须是转型门槛型的。根据这一发现,我们可以完善三个充分的条件,其中最佳动态配给政策属于门槛型(即关键配给水平 ) 。 为此,我们使用性能差异方程式来描述这一系统长期平均利润的单调性和最佳性,从而通过观察任何特定的参考政策,为最佳动态配给政策建立一些新的结构特性。最后,我们利用数字实验来展示我们最佳动态配给政策理论结果。 我们相信,本文中制定的方法和结果可以说明对配给队列进行的研究,并开启一系列可能很有希望的研究。