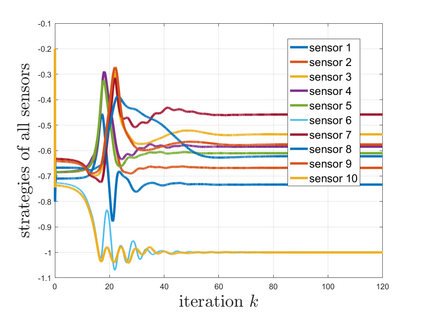
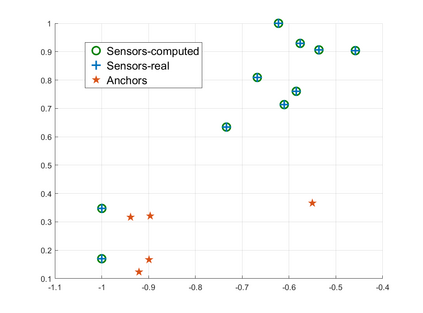
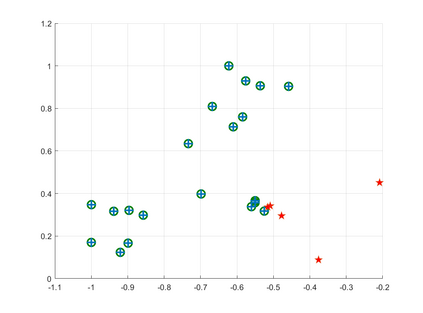
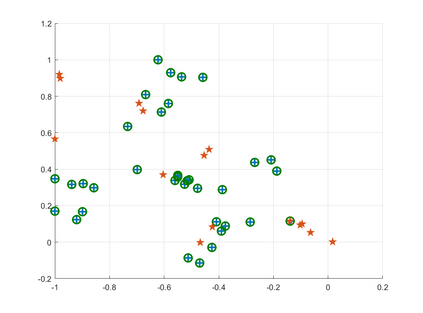
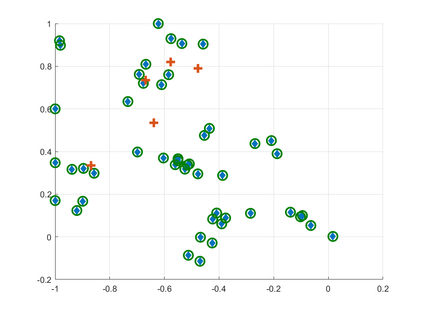
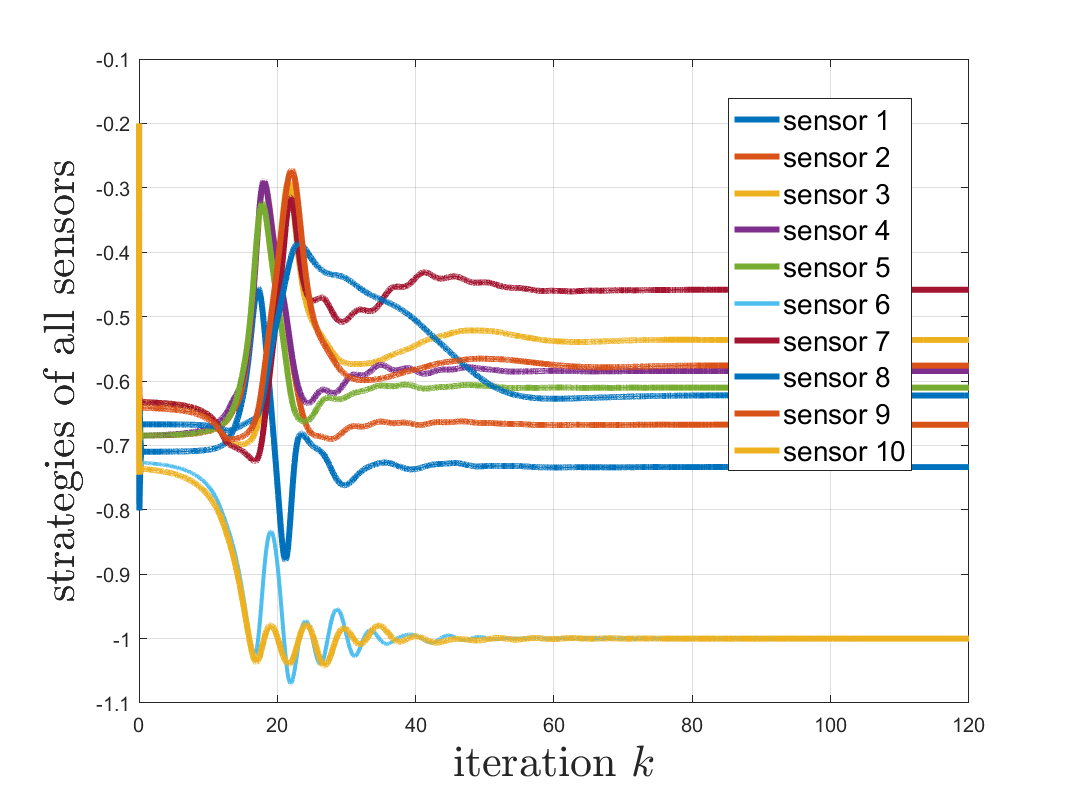
Sensor network localization (SNL) problems require determining the physical coordinates of all sensors in a network. This process relies on the global coordinates of anchors and the available measurements between non-anchor and anchor nodes. Attributed to the intrinsic non-convexity, obtaining a globally optimal solution to SNL is challenging, as well as implementing corresponding algorithms. In this paper, we formulate a non-convex multi-player potential game for a generic SNL problem to investigate the identification condition of the global Nash equilibrium (NE) therein, where the global NE represents the global solution of SNL. We employ canonical duality theory to transform the non-convex game into a complementary dual problem. Then we develop a conjugation-based algorithm to compute the stationary points of the complementary dual problem. On this basis, we show an identification condition of the global NE: the stationary point of the proposed algorithm satisfies a duality relation. Finally, simulation results are provided to validate the effectiveness of the theoretical results.
翻译:暂无翻译