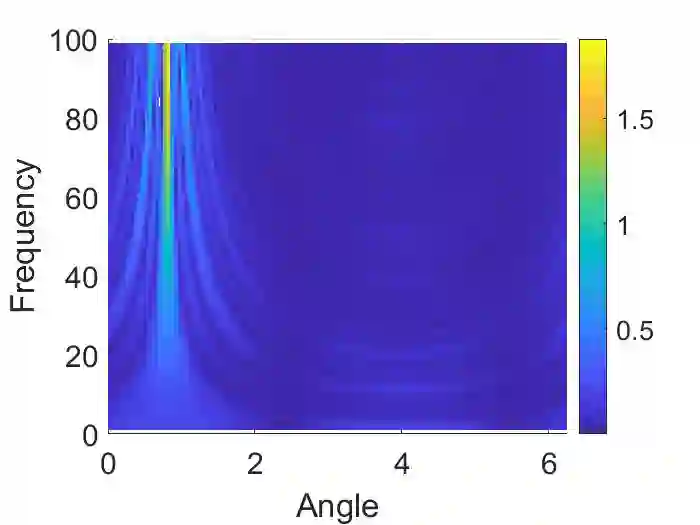
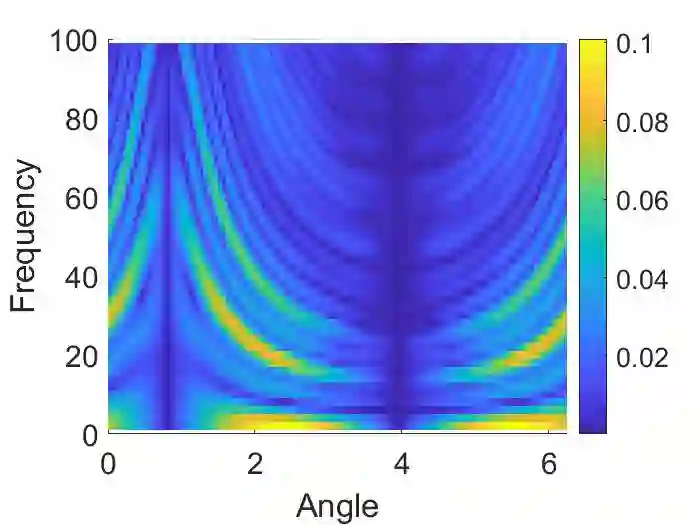
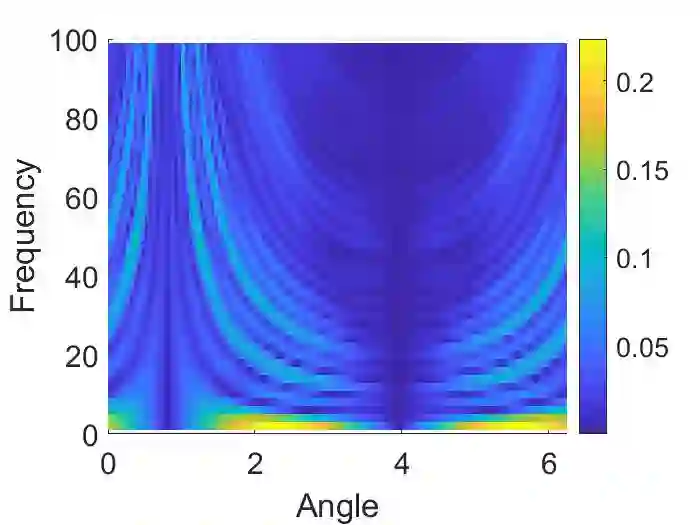
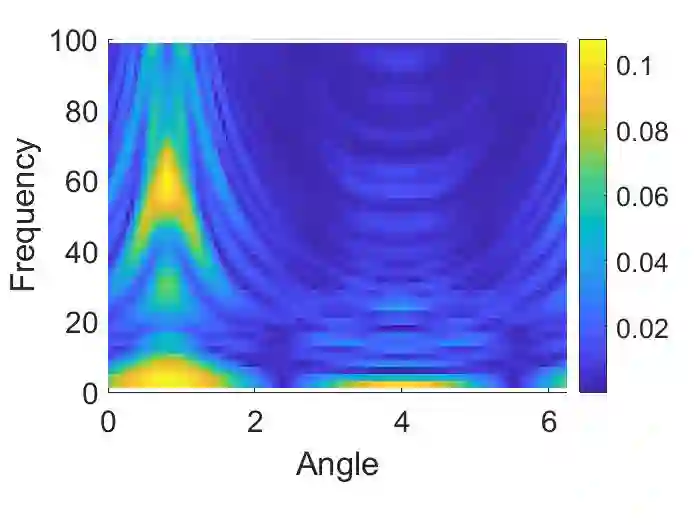
We propose a numerical method to approximate the scattering amplitudes for the elasticity system with a non-constant matrix potential in dimensions $d=2$ and $3$. This requires to approximate first the scattering field, for some incident waves, which can be written as the solution of a suitable Lippmann-Schwinger equation. In this work we adapt the method introduced by G. Vainikko in \cite{V} to solve such equations when considering the Lam\'e operator. Convergence is proved for sufficiently smooth potentials. Implementation details and numerical examples are also given.
翻译:我们提出一个数字方法,将弹性系统的散射振幅与非恒定矩阵潜力相近,在维度上为$d=2美元和$3美元。这要求首先对一些事件波的散射场进行近似,可以写成适当的Lipppmann-Schwinger等式的解决方案。在这项工作中,我们调整了G. Vainikko在\cite{V}中采用的方法,以便在考虑Lam\'e操作员时解决这些方程。一致性证明具有充分顺利的潜力。还给出了实施细节和数字实例。