Convergence, error analysis and longtime behavior of the Scalar Auxiliary Variable method for the nonlinear Schrödinger equation

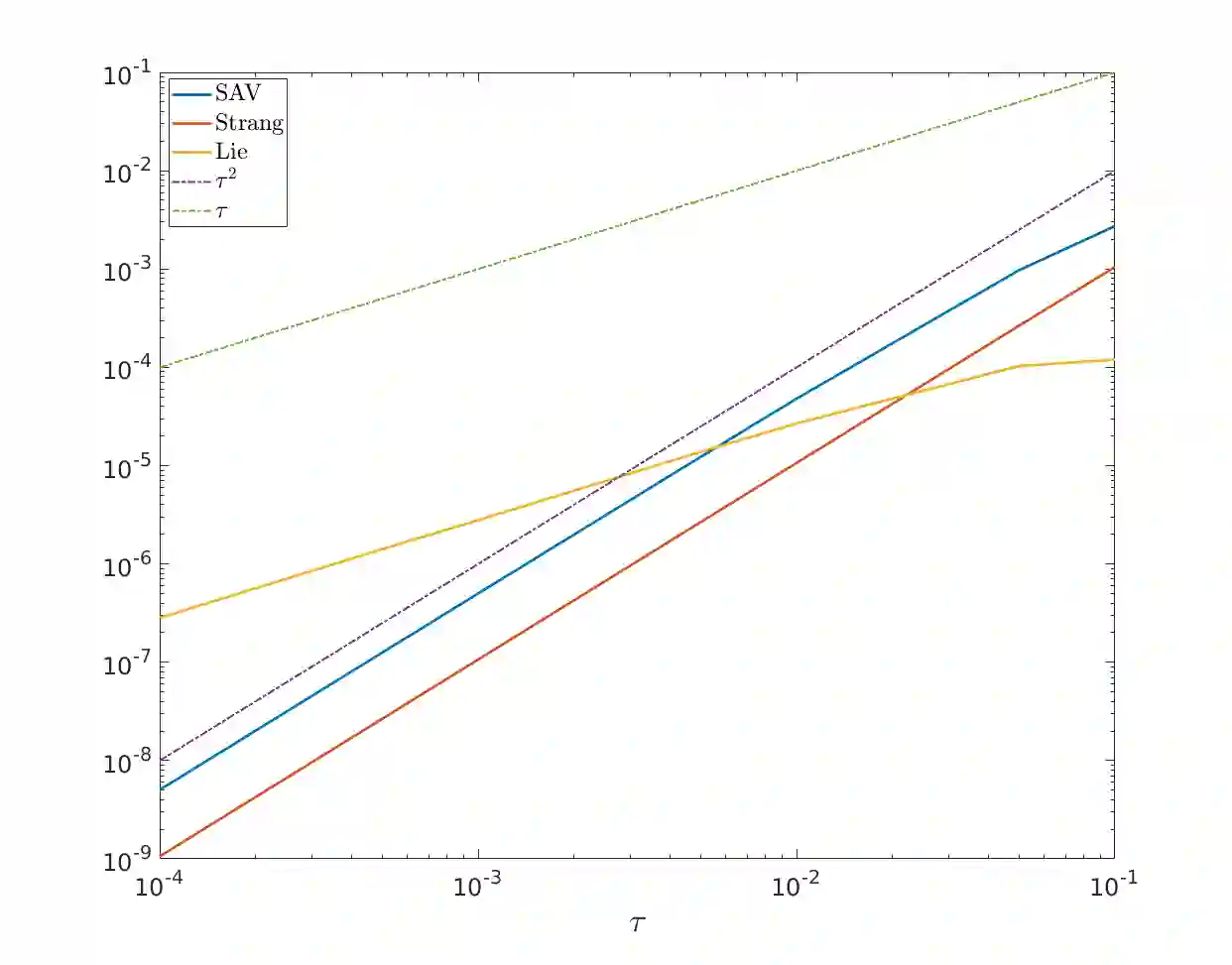
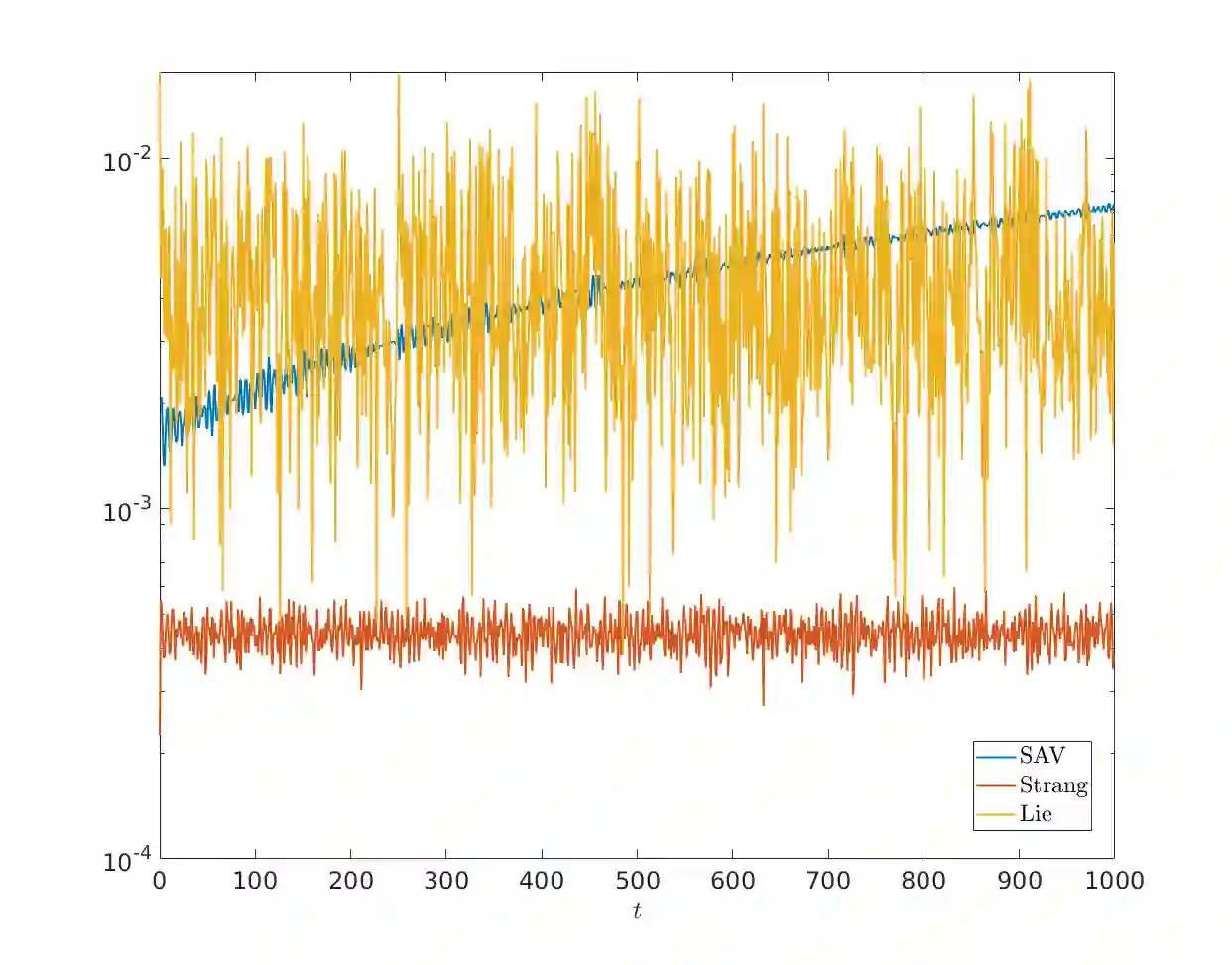
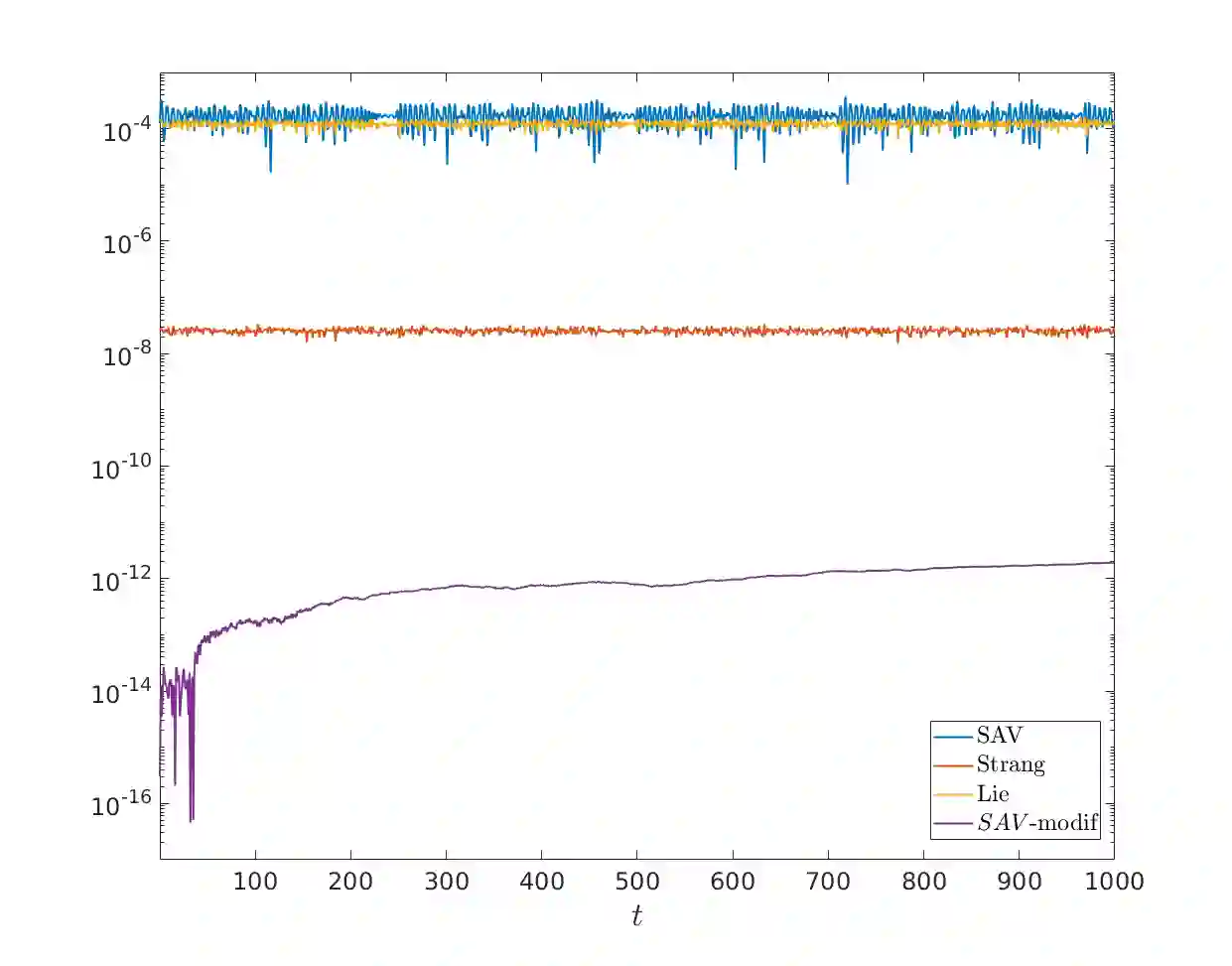
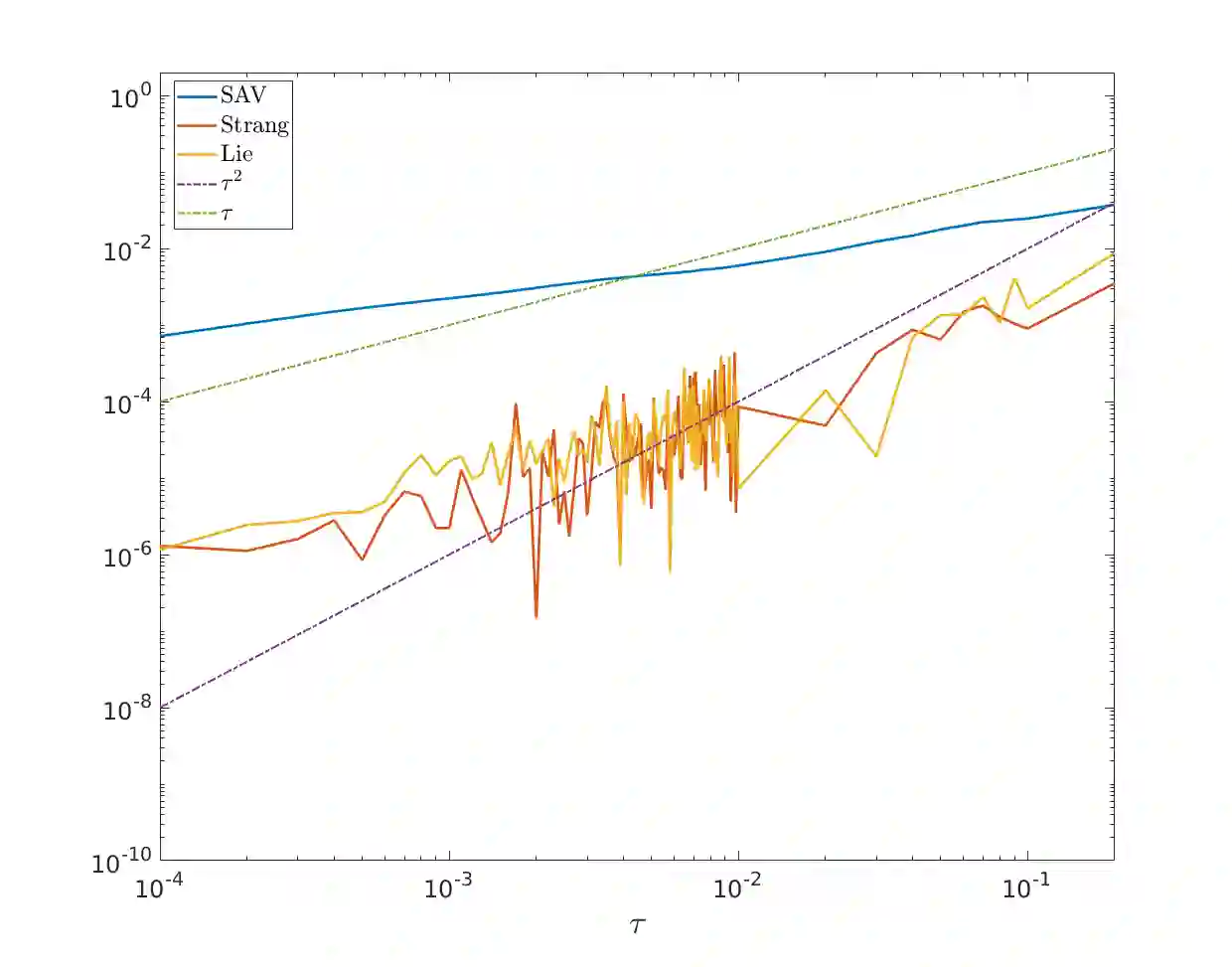
We carry out the convergence analysis of the Scalar Auxiliary Variable (SAV) method applied to the nonlinear Schr\"odinger equation which preserves a modified Hamiltonian on the discrete level. We derive a weak and strong convergence result, establish second-order global error bounds and present long time error estimates on the modified Hamiltonian. In addition, we illustrate the favorable energy conservation of the SAV method compared to classical splitting schemes in certain applications.