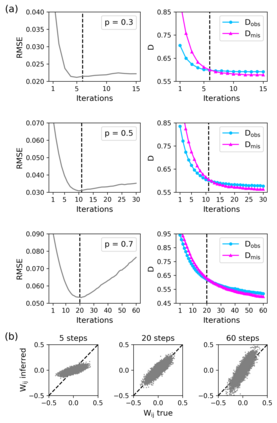
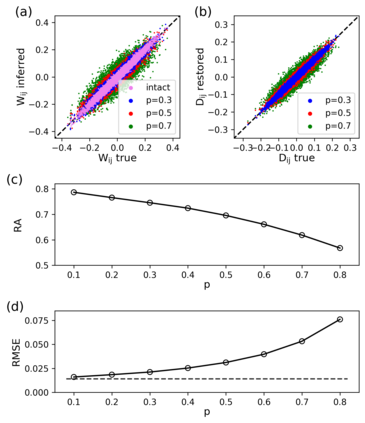
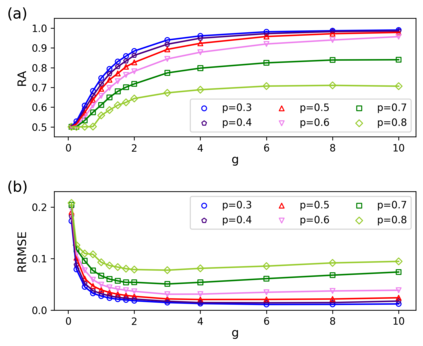
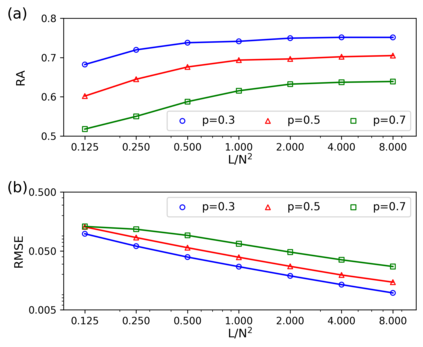
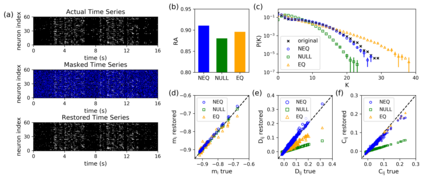
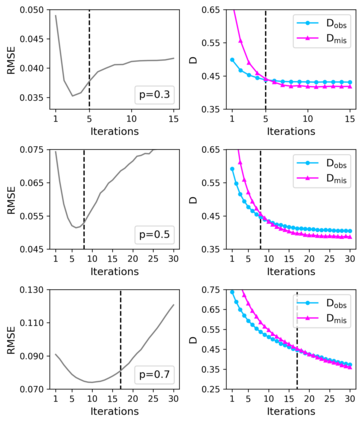
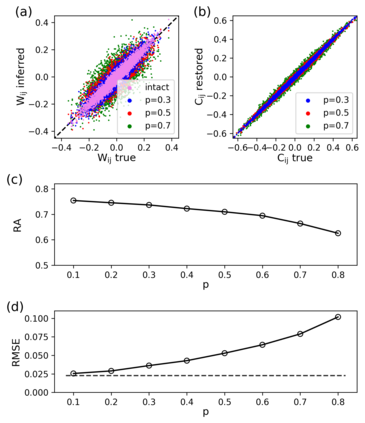
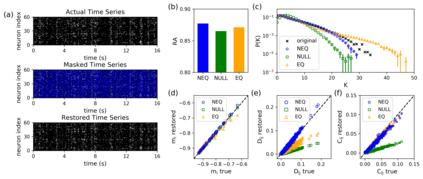
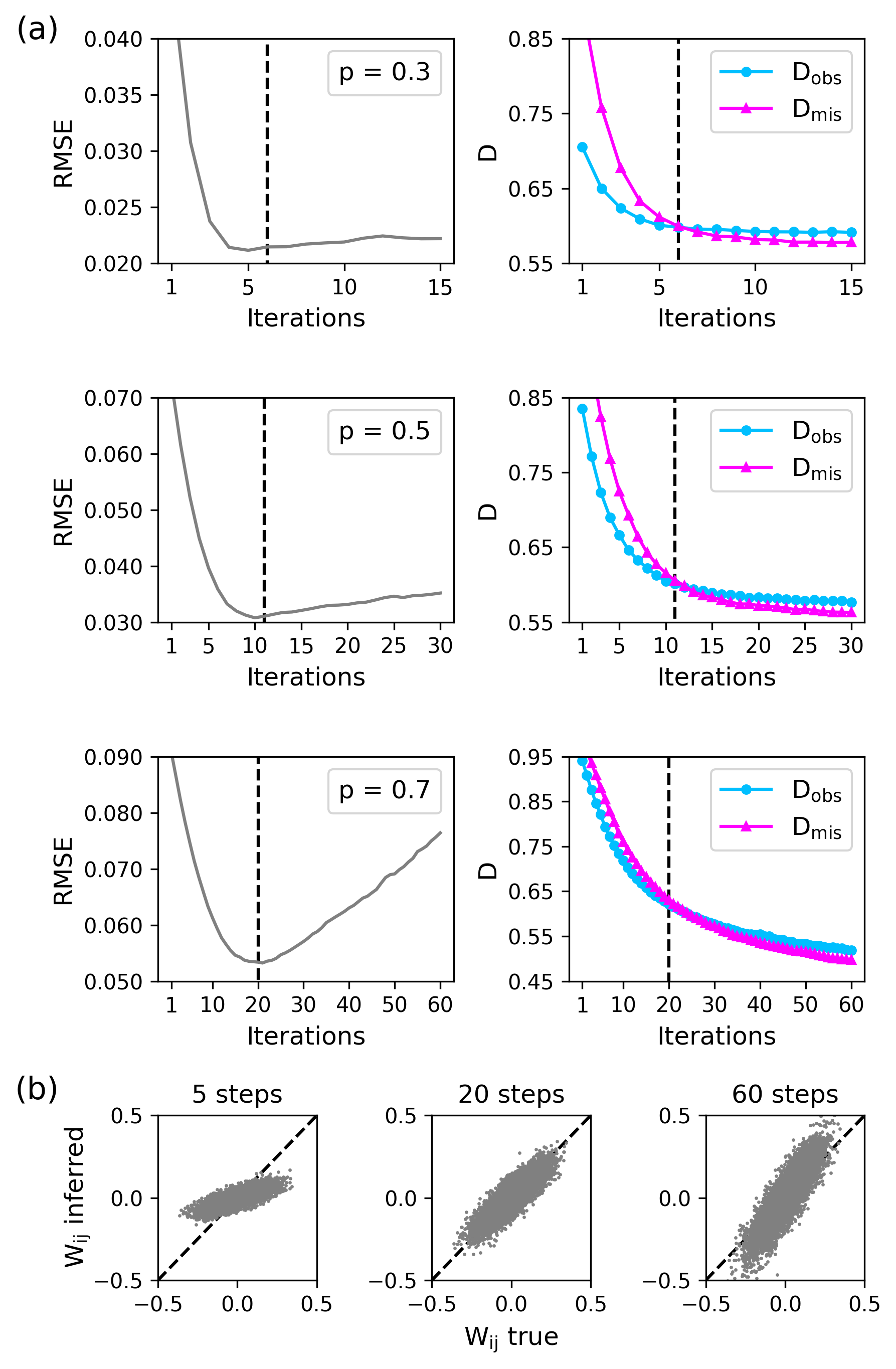
Inferring dynamics from time series is an important objective in data analysis. In particular, it is challenging to infer stochastic dynamics given incomplete data. We propose an expectation maximization (EM) algorithm that iterates between alternating two steps: E-step restores missing data points, while M-step infers an underlying network model of restored data. Using synthetic data generated by a kinetic Ising model, we confirm that the algorithm works for restoring missing data points as well as inferring the underlying model. At the initial iteration of the EM algorithm, the model inference shows better model-data consistency with observed data points than with missing data points. As we keep iterating, however, missing data points show better model-data consistency. We find that demanding equal consistency of observed and missing data points provides an effective stopping criterion for the iteration to prevent overshooting the most accurate model inference. Armed with this EM algorithm with this stopping criterion, we infer missing data points and an underlying network from a time-series data of real neuronal activities. Our method recovers collective properties of neuronal activities, such as time correlations and firing statistics, which have previously never been optimized to fit.
翻译:从时间序列中推断动态是数据分析的一个重要目标。特别是,从数据不完整的数据中推断出随机动态是具有挑战性的。我们建议了一种预期最大化算法,在交替两个步骤之间进行迭代:电子步骤恢复缺失的数据点,而M步骤推断出一个基础网络模型。使用动脉轴模型产生的合成数据,我们确认算法有助于恢复缺失的数据点并推断基本模型。在EM算法的初始迭代中,模型推论显示模型数据点与观察到的数据点比缺失的数据点更加一致。然而,随着我们不断进行迭代,缺失的数据点显示出更好的模型数据点的一致性。我们发现,要求所观察到和缺失的数据点的同等一致性为迭代提供了一个有效的停止标准,以防止过度解析最准确的模型推论。我们用这种停止标准的算法,从真实神经活动的时间序列数据中推断出缺失的数据点和基础网络更加一致。我们的方法恢复了神经系统活动的集体特性,如以往从未与发射时序数据一样,因此与时间相适应。