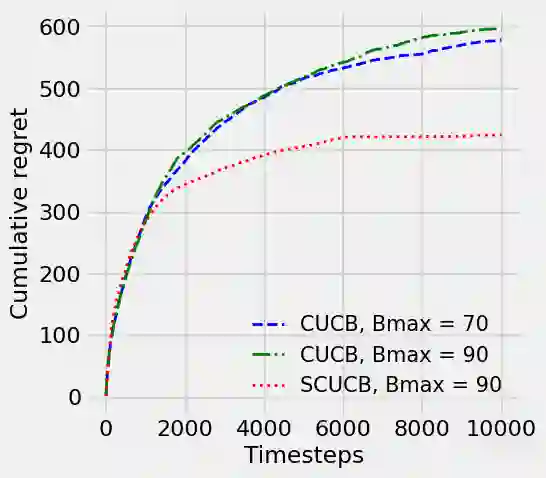
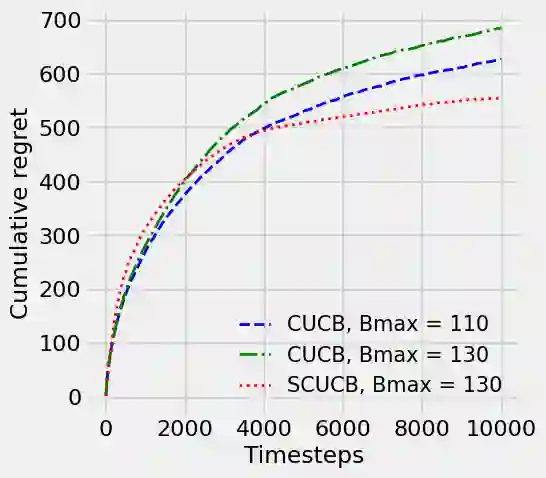
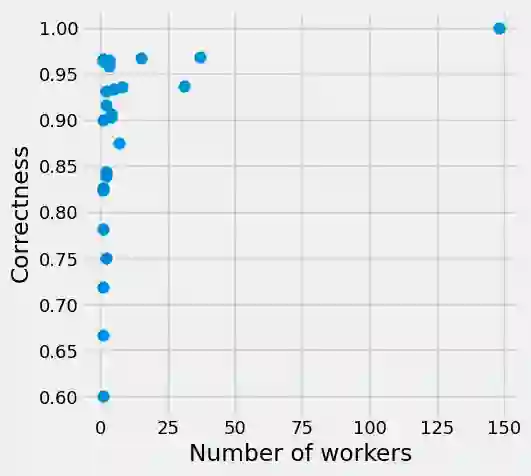
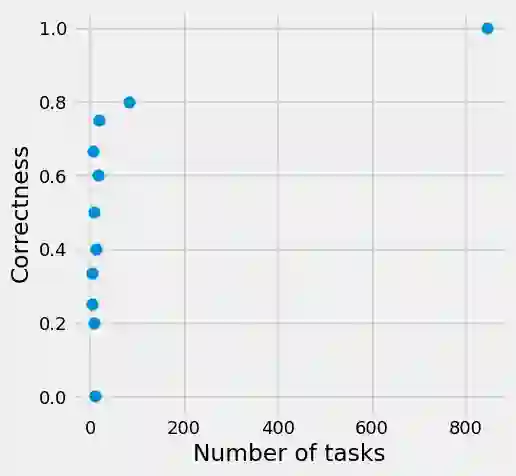
Strategic behavior against sequential learning methods, such as "click framing" in real recommendation systems, have been widely observed. Motivated by such behavior we study the problem of combinatorial multi-armed bandits (CMAB) under strategic manipulations of rewards, where each arm can modify the emitted reward signals for its own interest. This characterization of the adversarial behavior is a relaxation of previously well-studied settings such as adversarial attacks and adversarial corruption. We propose a strategic variant of the combinatorial UCB algorithm, which has a regret of at most $O(m\log T + m B_{max})$ under strategic manipulations, where $T$ is the time horizon, $m$ is the number of arms, and $B_{max}$ is the maximum budget of an arm. We provide lower bounds on the budget for arms to incur certain regret of the bandit algorithm. Extensive experiments on online worker selection for crowdsourcing systems, online influence maximization and online recommendations with both synthetic and real datasets corroborate our theoretical findings on robustness and regret bounds, in a variety of regimes of manipulation budgets.
翻译:对抗性行为的特征是放松了先前研究周密的环境,如对抗性攻击和对抗性腐败。我们提出了一个组合式UCB算法的战略变体,该算法对在战略操纵下花费最多为$O(m\log T+m B ⁇ max})的负数($O(m\log T+m B ⁇ max})的负数($T)的负数($T)是时间范围,$m是武器的数量,$B ⁇ max}是武器的最大预算。我们提供了较低的武器预算约束,以引起强盗算法的某些遗憾。我们用合成和真实数据集对在线工人选择众包系统、在线影响最大化和在线建议进行了广泛的实验,证实了我们在各种操纵预算制度中对稳健和遗憾界限的理论结论。