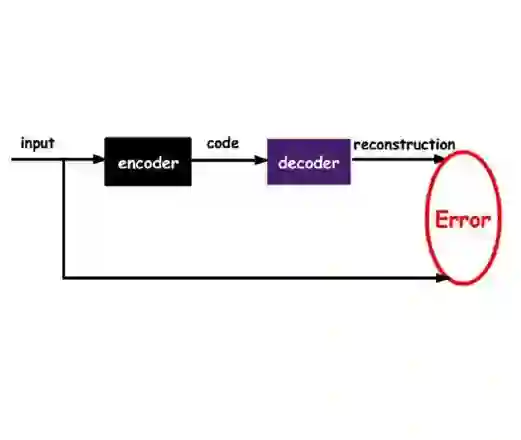
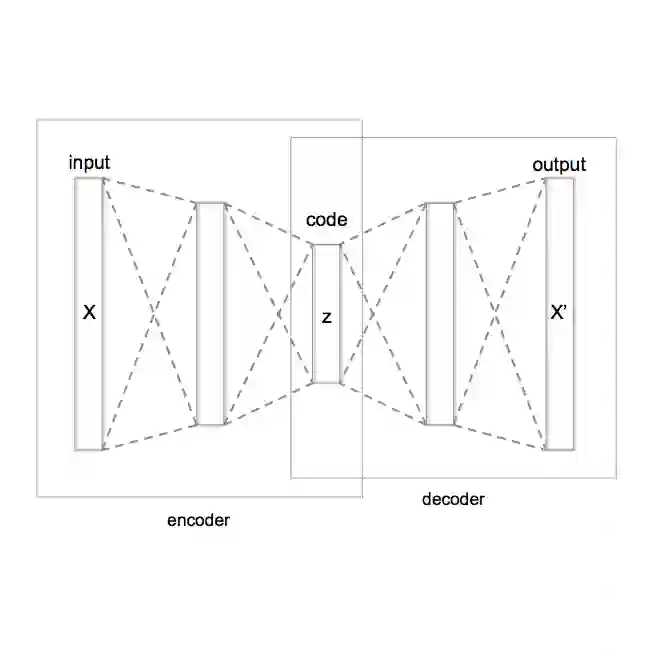
Graph Neural Networks (GNNs) and Variational Autoencoders (VAEs) have been widely used in modeling and generating graphs with latent factors. However, there is no clear explanation of what these latent factors are and why they perform well. In this work, we present Dirichlet Graph Variational Autoencoder (DGVAE) with graph cluster memberships as latent factors. Our study connects VAEs based graph generation and balanced graph cut, and provides a new way to understand and improve the internal mechanism of VAEs based graph generation. Specifically, we first interpret the reconstruction term of DGVAE as balanced graph cut in a principled way. Furthermore, motivated by the low pass characteristics in balanced graph cut, we propose a new variant of GNN named Heatts to encode the input graph into cluster memberships. Heatts utilizes the Taylor series for fast computation of heat kernels and has better low pass characteristics than Graph Convolutional Networks (GCN). Through experiments on graph generation and graph clustering, we demonstrate the effectiveness of our proposed framework.
翻译:在模拟和生成带有潜在因素的图形时,广泛使用神经网络和动态自动电解码器(VAEs)来模拟和生成带有潜伏因素的图形,但是,对这些潜在因素是什么以及为什么它们表现良好没有清楚的解释。在这项工作中,我们将Drichlet 图形自动电解码器(DGVAE)与图形群成份作为潜伏因素。我们的研究将基于VAEs的图形生成和平衡的图形切割联系起来,并提供了理解和改进基于VAEs的图形生成的内部机制的新方法。具体地说,我们首先将这些DGVAE的重建术语解释为以有原则的方式削减的平衡的图形。此外,由于平衡的图形切割中的低通过特性,我们提出了名为Heatts的GNNNN的新变量,将输入图编码为集成成份。Heatts利用泰勒系列快速计算热内核和比图形革命网络(GCN)更低的通过特性。我们通过对图形生成和图形组合的实验,展示了我们提议的框架的有效性。