Deep Neural Networks Guided Ensemble Learning for Point Estimation in Finite Samples

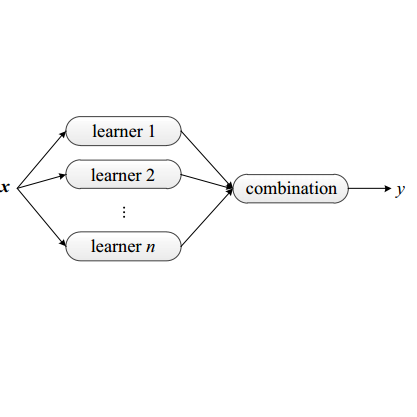
As one of the most important estimators in classical statistics, the uniformly minimum variance unbiased estimator (UMVUE) has been adopted for point estimation in many statistical studies, especially for small sample problems. Moving beyond typical settings in the exponential distribution family, it is usually challenging to prove the existence and further construct such UMVUE in finite samples. For example in the ongoing Adaptive COVID-19 Treatment Trial (ACTT), it is hard to characterize the complete sufficient statistics of the underlying treatment effect due to pre-planned modifications to design aspects based on accumulated unblinded data. As an alternative solution, we propose a Deep Neural Networks (DNN) guided ensemble learning framework to construct an improved estimator from existing ones. We show that our estimator is consistent and asymptotically reaches the minimal variance within the class of linearly combined estimators. Simulation studies are further performed to demonstrate that our proposed estimator has considerable finite-sample efficiency gain. In the ACTT on COVID-19 as an important application, our method essentially contributes to a more ethical and efficient adaptive clinical trial with fewer patients enrolled.