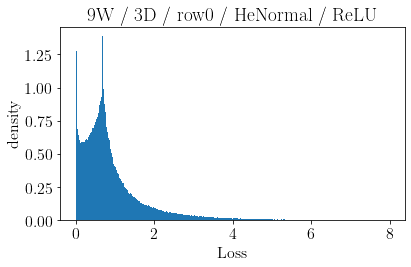
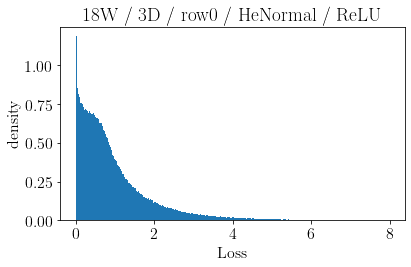
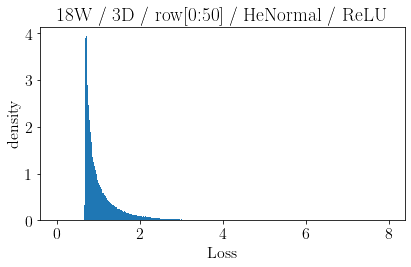
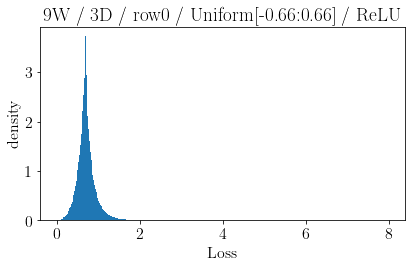
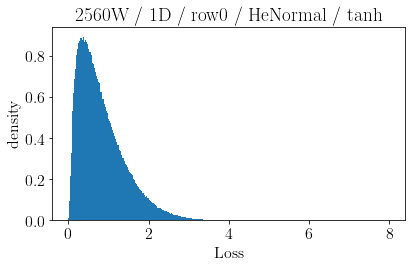
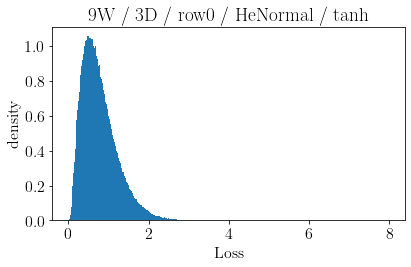
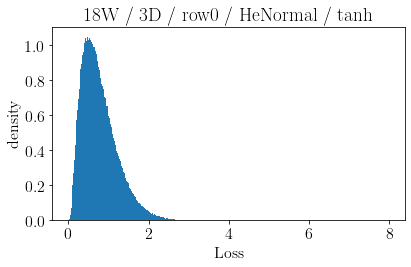
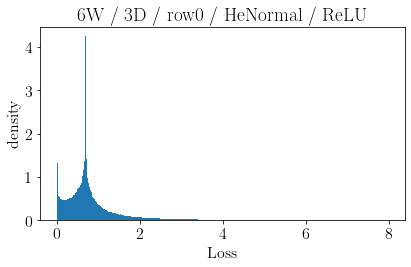
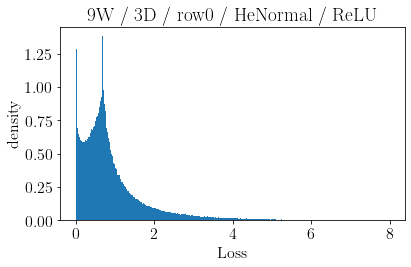
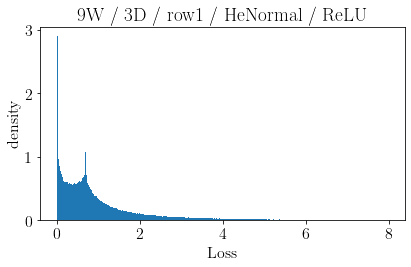
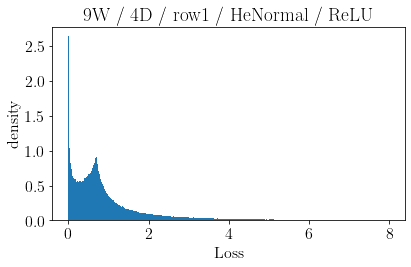
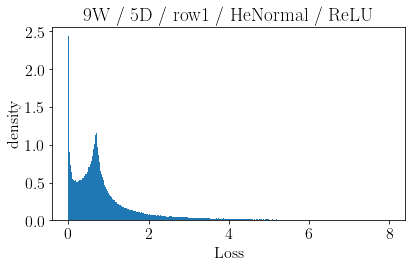
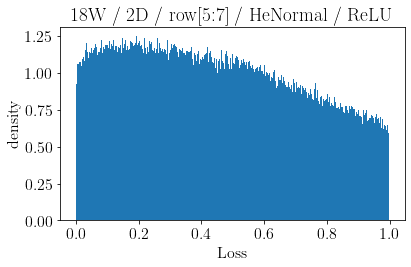
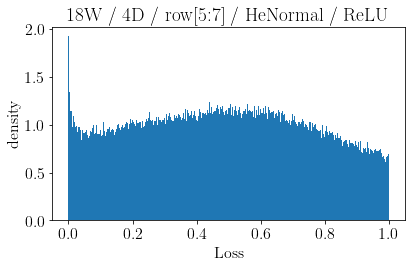
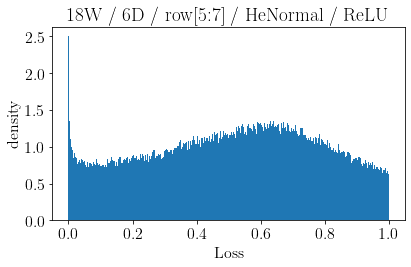
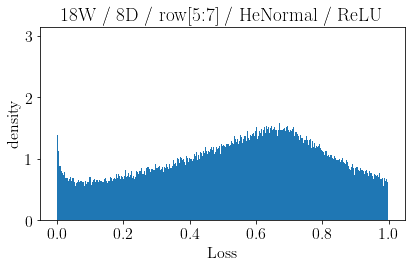
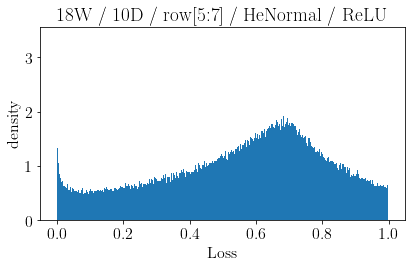
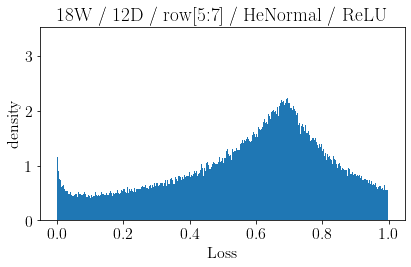
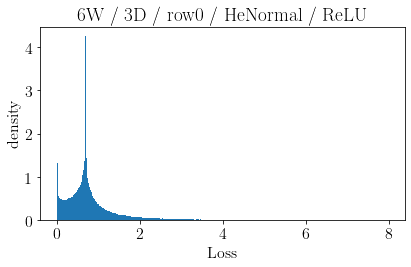
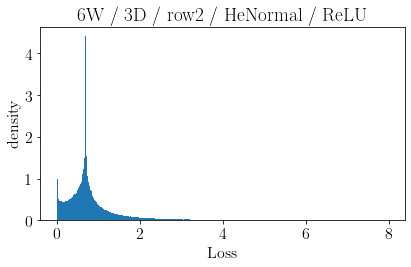
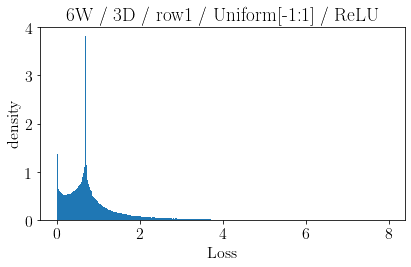
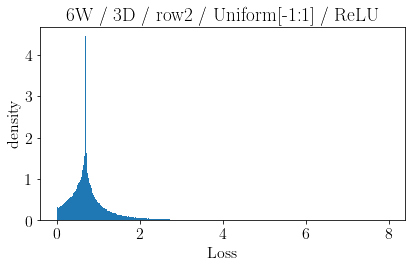
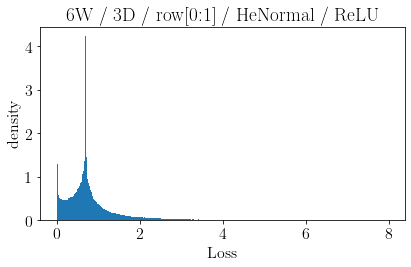
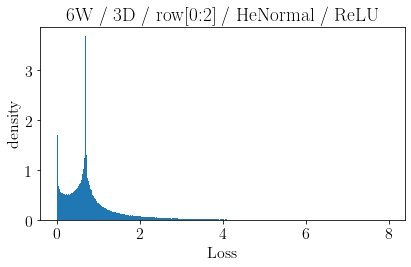
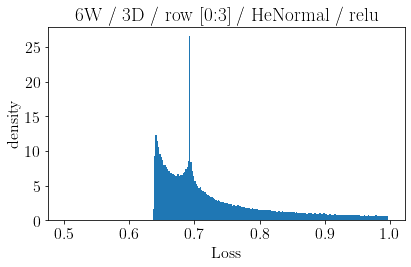
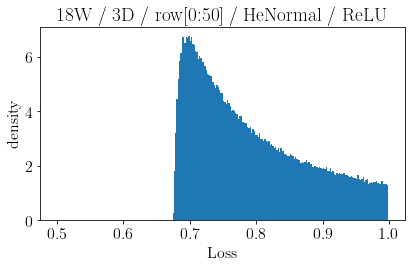
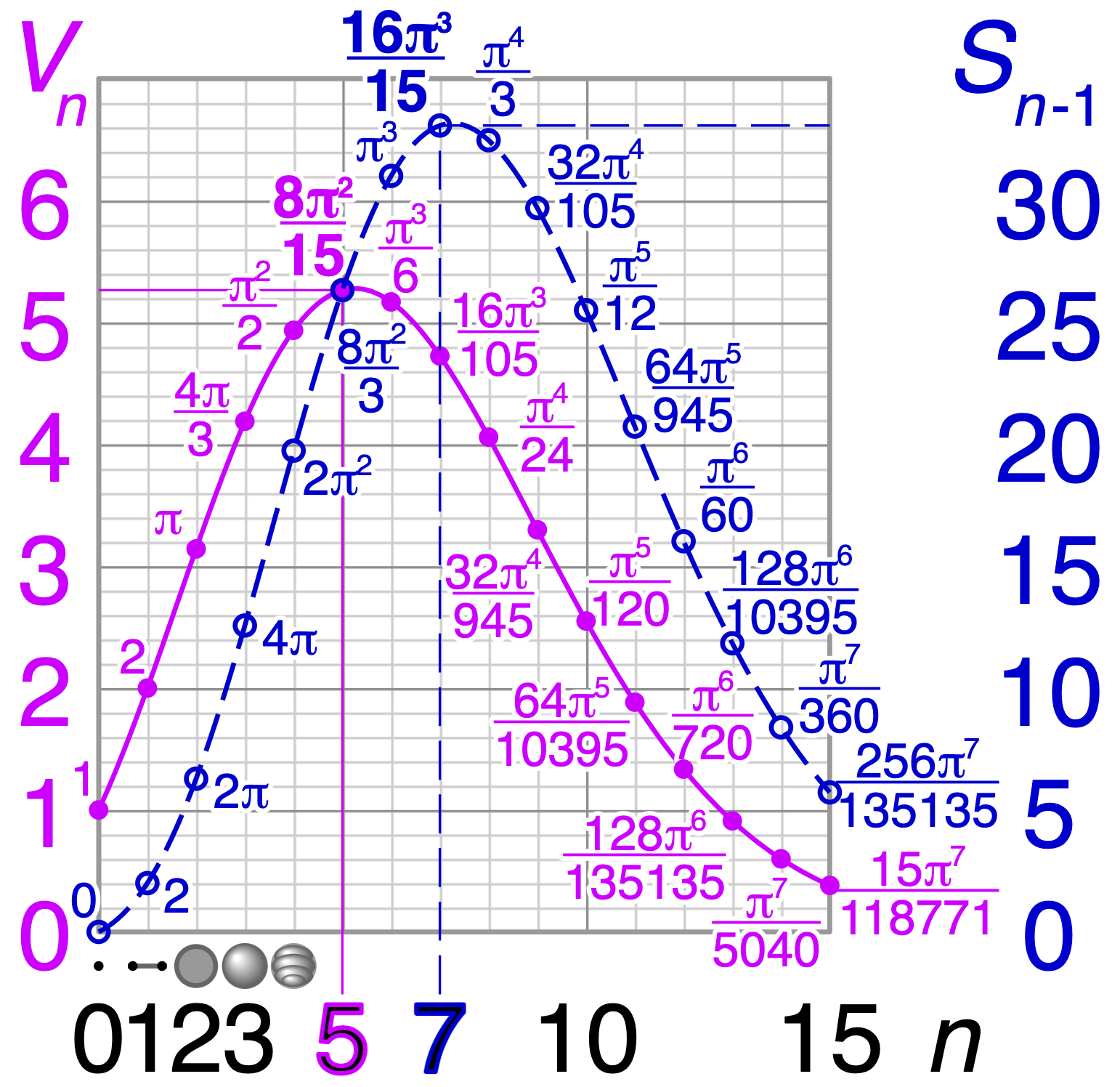
The volume of the distribution of possible weight configurations associated with a loss value may be the source of implicit regularization from overparameterization due to the phenomenon of contracting volume with increasing dimensions for geometric figures demonstrated by hyperspheres. This paper introduces geometric regularization and explores potential applicability to several unexplained phenomenon including double descent, the differences between wide and deep networks, the benefits of He initialization and retained proximity in training, gradient confusion, fitness landscape properties, double descent in other learning paradigms, and other findings for overparameterized learning. Experiments are conducted by aggregating histograms of loss values corresponding to randomly sampled initializations in small setups, which find directional correlations in zero or central mode dominance from deviations in width, depth, and initialization distributions. Double descent is likely due to a regularization phase change when a training path reaches low enough loss that the loss manifold volume contraction from a reduced range of potential weight sets is amplified by an overparameterized geometry.
翻译:与损失价值相关的可能重量配置分布量的分布可能是由于超高参数化现象造成的超度化的隐性正规化现象,其原因可能是超光速显示的几何数字在数量上呈日益扩大的收缩现象。本文介绍了几何正规化,并探讨了若干无法解释的现象的潜在适用性,包括双向下降、广度和深度网络之间的差异、He初始化的好处和在培训中保持接近性、梯度混乱、健康景观特性、其他学习模式中的双度下降以及超度化学习的其他发现。实验通过将小装置随机抽样初始化相应的损失值直方图汇总进行实验,这些小装置从宽度、深度和初始化分布的偏差中发现零度或中位模式主导度。如果培训路径达到足够低的损失程度,可能使减少的潜在重力组合体积损失因过度的几何测量而加剧,则可能发生双重下降。