Learning of Causal Observable Functions for Koopman-DFL Lifting Linearization of Nonlinear Controlled Systems and Its Application to Excavation Automation

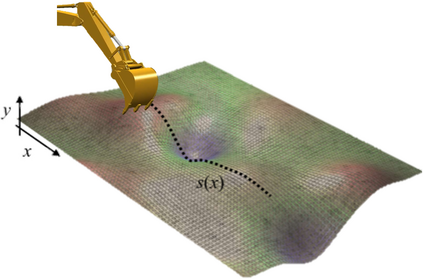
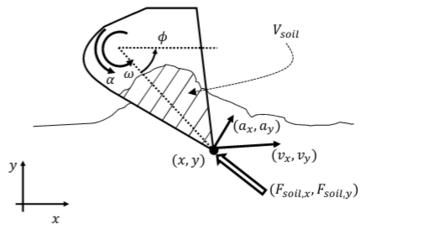
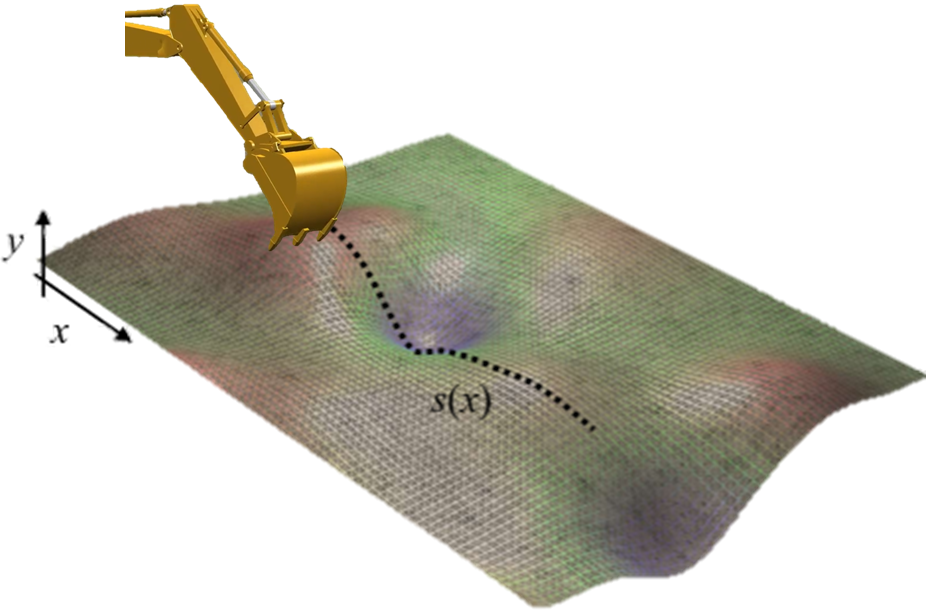
Effective and causal observable functions for low-order lifting linearization of nonlinear controlled systems are learned from data by using neural networks. While Koopman operator theory allows us to represent a nonlinear system as a linear system in an infinite-dimensional space of observables, exact linearization is guaranteed only for autonomous systems with no input, and finding effective observable functions for approximation with a low-order linear system remains an open question. Dual Faceted Linearization uses a set of effective observables for low-order lifting linearization, but the method requires knowledge of the physical structure of the nonlinear system. Here, a data-driven method is presented for generating a set of nonlinear observable functions that can accurately approximate a nonlinear control system to a low-order linear control system. A caveat in using data of measured variables as observables is that the measured variables may contain input to the system, which incurs a causality contradiction when lifting the system, i.e. taking derivatives of the observables. The current work presents a method for eliminating such anti-causal components of the observables and lifting the system using only causal observables. The method is applied to excavation automation, a complex nonlinear dynamical system, to obtain a low-order lifted linear model for control design.