Combinatorics of Reduced Ordered Binary Decision Diagrams: Application to uniform random sampling

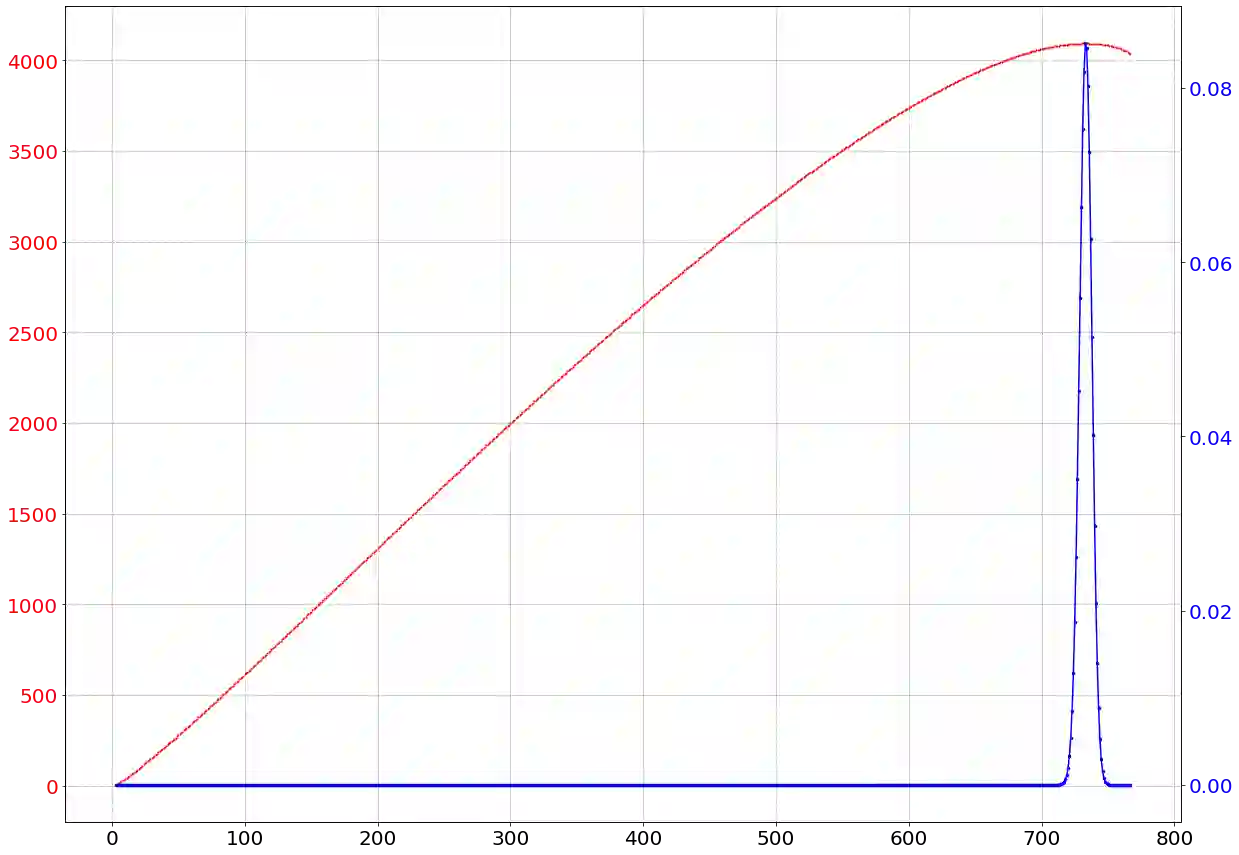
Since three decades binary decision diagrams, representing efficiently Boolean functions, are widely used, in many distinct contexts like model verification, machine learning. The most famous variant, called reduced ordered binary decision diagram (ROBDD for short), can be viewed as the result of a compaction procedure on the full decision tree. In this paper we aim at computing the exact distribution of the Boolean functions in $k$~variables according to the ROBDD size, where the ROBDD size is equal to the size of the underlying directed acyclic graph (DAG) structure. Recall the number of Boolean functions is equal to $2^{2^k}$, which is of double exponential growth; hence a combinatorial explosion is to be expected. The maximal size of a ROBDD with $k$ variables is $M_k \sim 2^k / k$ and thus, the support of the ROBDD size distribution is also of length $M_k$, making $M_k$ a natural complexity unit for our problem. In this paper, we develop the first polynomial algorithm to derive the distribution of the Boolean functions with respect to their ROBDD sizes. The algorithm is essentially quartic in $M_k$ for the time complexity and quadratic for the space complexity. The main obstacle is to take into account dependencies inside the DAG structure, and we propose a new combinatorial counting procedure reminiscent of the inclusion-exclusion principle. As a by-product, we present an efficient polynomial unranking algorithm for ROBDDs, which in turn yields a uniform random sampler over the set of ROBDDs of a given size or of a given profile. This is a great improvement to the uniform sampler over the set of all Boolean functions in $k$ variables. Indeed, due to the Shannon effect, the uniform distribution over Boolean functions is heavily biased to extremely complex functions, with near maximal ROBDD size, thus preventing to sample small ROBDDs