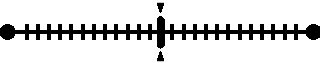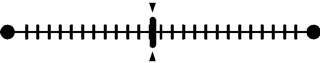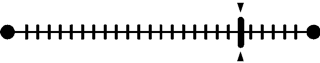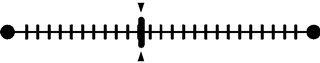深入机器学习系列之：隐式狄利克雷分布(1)

会员服务 ·

深入机器学习系列之：隐式狄利克雷分布(1)

2018 年 12 月 27 日 数据猿

导读

这一系列我们将会分两篇推送来详细介绍隐式狄利克雷分布，今天为大家带来LDA的数学预备知识以及LDA主题模型的介绍。

来源：星环科技丨作者： endymecy

数据猿官网 | www.datayuan.cn

今日头条丨一点资讯丨腾讯丨搜狐丨网易丨凤凰丨阿里UC大鱼丨新浪微博丨新浪看点丨百度百家丨博客中国丨趣头条丨腾讯云·云+社区

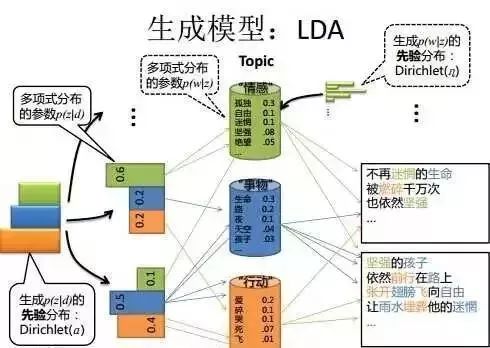
LDA是一种概率主题模型：隐式狄利克雷分布（Latent Dirichlet Allocation，简称LDA）。LDA是2003年提出的一种主题模型，它可以将文档集中每篇文档的主题以概率分布的形式给出。通过分析一些文档，我们可以抽取出它们的主题（分布），根据主题（分布）进行主题聚类或文本分类。同时，它是一种典型的词袋模型，即一篇文档是由一组词构成，词与词之间没有先后顺序的关系。一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

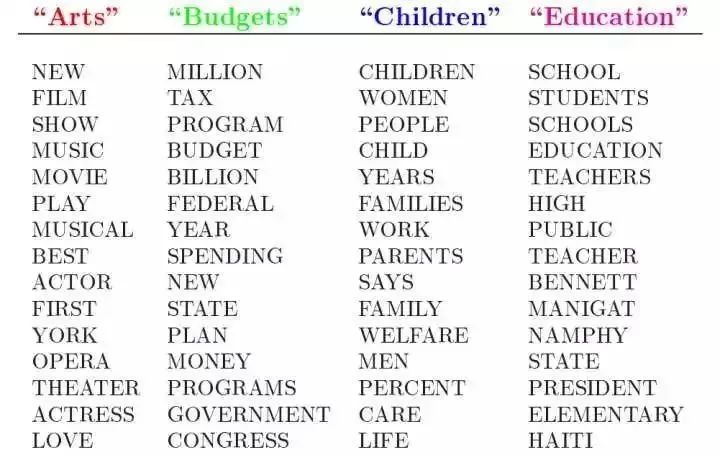
举一个简单的例子，比如假设事先给定了这几个主题：Arts、Budgets、Children、Education，然后通过学习的方式，获取每个主题Topic对应的词语，如下图所示：

然后以一定的概率选取上述某个主题，再以一定的概率选取那个主题下的某个单词，不断的重复这两步，最终生成如下图所示的一篇文章（不同颜色的词语分别表示不同主题）。

我们看到一篇文章后，往往会推测这篇文章是如何生成的，我们通常认为作者会先确定几个主题，然后围绕这几个主题遣词造句写成全文。LDA要干的事情就是根据给定的文档，判断它的主题分布。在LDA模型中，生成文档的过程有如下几步：

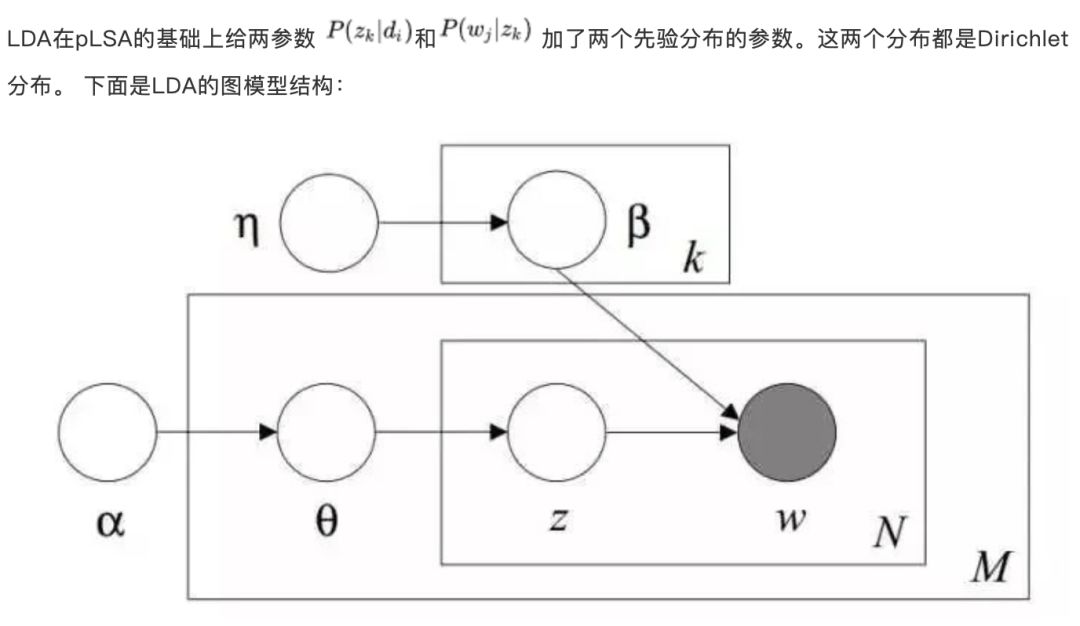
LDA的图模型结构如下图所示：

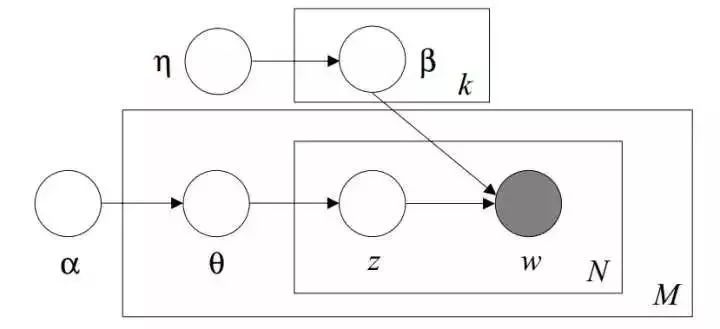
LDA会涉及很多数学知识，后面的章节我会首先介绍LDA涉及的数学知识，然后在这些数学知识的基础上详细讲解LDA的原理。

1数学预备

1.1 Gamma函数

在高等数学中，有一个长相奇特的Gamma函数

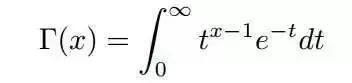
通过分部积分，可以推导gamma函数有如下递归性质

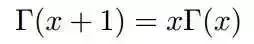
通过该递归性质，我们可以很容易证明，gamma函数可以被当成阶乘在实数集上的延拓，具有如下性质

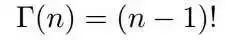
1.2 Digamma函数

如下函数被称为Digamma函数，它是Gamma函数对数的一阶导数

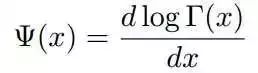
这是一个很重要的函数，在涉及Dirichlet分布相关的参数的极大似然估计时，往往需要用到这个函数。Digamma函数具有如下一个漂亮的性质

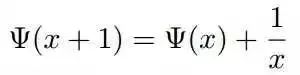
1.3 二项分布（Binomial distribution）

二项分布是由伯努利分布推出的。伯努利分布，又称两点分布或0-1分布，是一个离散型的随机分布，其中的随机变量只有两类取值，即0或者1。二项分布是重复n次的伯努利试验。简言之，只做一次实验，是伯努利分布，重复做了n次，是二项分布。二项分布的概率密度函数为：

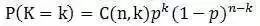
对于k=1,2，...,n，其中C(n,k)是二项式系数（这就是二项分布的名称的由来）

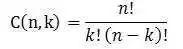
1.4 多项分布

多项分布是二项分布扩展到多维的情况。多项分布是指单次试验中的随机变量的取值不再是0-1，而是有多种离散值可能（1,2,3...,k）。比如投掷6个面的骰子实验，N次实验结果服从K=6的多项分布。其中：

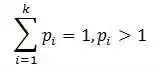
多项分布的概率密度函数为：

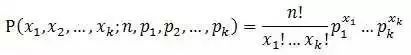
1.5 Beta分布

1.5.1 Beta分布

首先看下面的问题1（问题1到问题4都取自于文献【1】）。

问题1：

为解决这个问题，可以尝试计算落在区间[x,x+delta x]的概率。首先，把[0,1]区间分成三段[0,x),[x,x+delta x]，(x+delta x,1]，然后考虑下简单的情形：即假设n个数中只有1个落在了区间[x,x+delta x]内，由于这个区间内的数X(k)是第k大的，所以[0,x)中应该有k−1个数，(x+delta x,1]这个区间中应该有n−k个数。如下图所示：

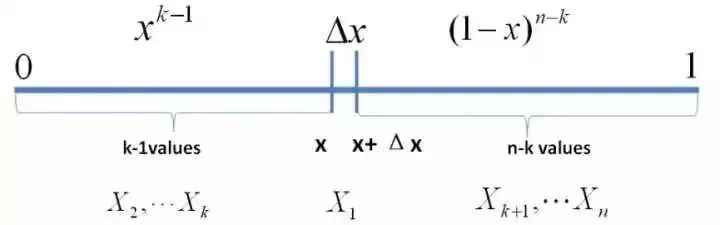
上述问题可以转换为下述事件E：

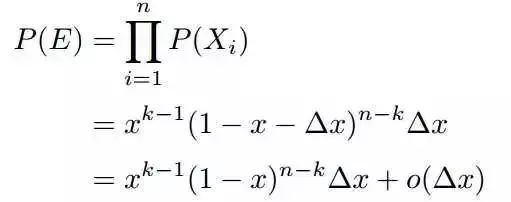
对于上述事件E，有：

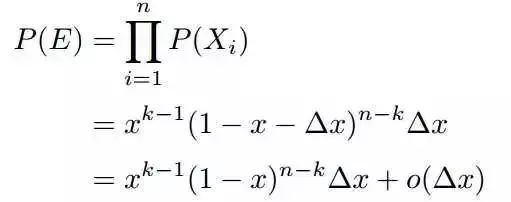
其中，o(delta x)表示delta x的高阶无穷小。显然，由于不同的排列组合，即n个数中有一个落在[x,x+delta x]区间的有n种取法，余下n−1个数中有k−1个落在[0,x)的有C(n-1,k-1)种组合。所以和事件E等价的事件一共有nC(n-1,k-1)个。

文献【1】中证明，只要落在[x,x+delta x]内的数字超过一个，则对应的事件的概率就是o(delta x)。所以的概率密度函数为：

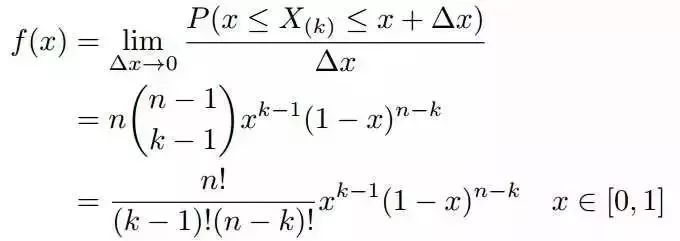
利用Gamma函数，我们可以将f(x)表示成如下形式：

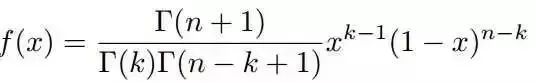
在上式中，我们用alpha=k，beta=n-k+1替换，可以得到beta分布的概率密度函数

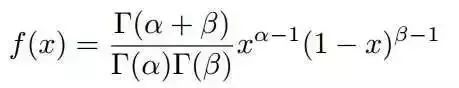
1.5.2 共轭先验分布

什么是共轭呢？轭的意思是束缚、控制。共轭从字面上理解，则是共同约束，或互相约束。在贝叶斯概率理论中，如果后验概率P(z|x)和先验概率p(z)满足同样的分布，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

1.5.3 Beta-Binomial 共轭

我们在问题1的基础上增加一些观测数据，变成问题2：

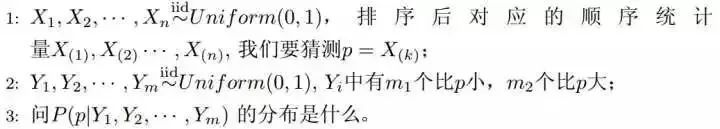
根据1.5.1的介绍，我们知道事件p服从beta分布,它的概率密度函数为：

按照贝叶斯推理的逻辑，把以上过程整理如下：

1、p是我们要猜测的参数，我们推导出p的分布为f(p)=Beta(p|k,n-k+1),称为p的先验分布

2、根据Yi中有m1个比p小，有m2个比p大，Yi相当是做了m次伯努利实验，所以m1服从二项分布B(m,p)

3、在给定了来自数据提供(m1,m2)知识后，p的后验分布变为f(p|m1,m2)=Beta(p|k+m1,n-k+1+m2)

贝叶斯估计的基本过程是：

先验分布 + 数据的知识 = 后验分布

以上贝叶斯分析过程的简单直观的表示就是：

Beta(p|k,n-k+1) + BinomCount(m1,m2) = Beta(p|k+m1,n-k+1+m2)

更一般的，对于非负实数alpha和beta，我们有如下关系：

Beta(p|alpha,beta) + BinomCount(m1,m2) = Beta(p|alpha+m1,beta+m2)

针对于这种观测到的数据符合二项分布，参数的先验分布和后验分布都是Beta分布的情况，就是Beta-Binomial共轭。换言之，Beta分布是二项式分布的共轭先验概率分布。二项分布和Beta分布是共轭分布意味着，如果我们为二项分布的参数p选取的先验分布是Beta分布，那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布。

1.6 Dirichlet 分布

1.6.1 Dirichlet 分布

Dirichlet分布，是beta分布在高维度上的推广。Dirichlet分布的的密度函数形式跟beta分布的密度函数类似：

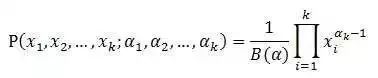
其中

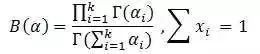
至此，我们可以看到二项分布和多项分布很相似，Beta分布和Dirichlet分布很相似。并且Beta分布是二项式分布的共轭先验概率分布。那么Dirichlet分布呢？Dirichlet分布是多项式分布的共轭先验概率分布。下文来论证这点。

1.6.2 Dirichlet-Multinomial 共轭

在1.5.3章问题2的基础上，我们更进一步引入问题3：

类似于问题1的推导，我们可以容易推导联合分布。为了简化计算，我们取x3满足x1+x2+x3=1,x1和x2是变量。如下图所示。

概率计算如下：

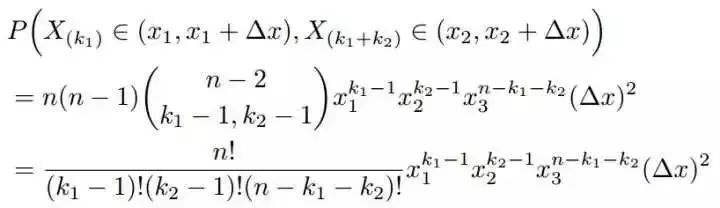
于是我们得到联合分布为：

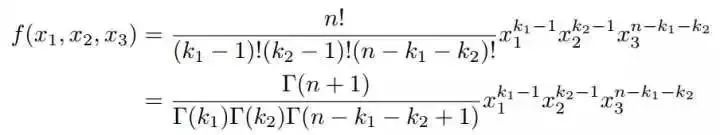
观察上述式子的最终结果，可以看出上面这个分布其实就是3维形式的Dirichlet分布。令alpha1=k1,alpha2=k2,alpha3=n-k1-k2+1，分布密度函数可以写为：

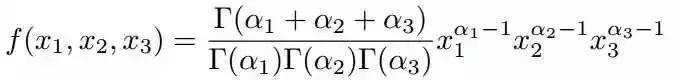
为了论证Dirichlet分布是多项式分布的共轭先验概率分布，在上述问题3的基础上再进一步，提出问题4。

为了方便计算，我们记

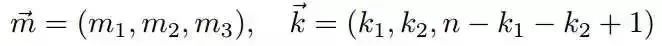
根据问题中的信息，我们可以推理得到p1,p2在X;Y这m+n个数中分别成为了第k1+m1,k1+k2+m1+m2大的数。后验分布p应该为

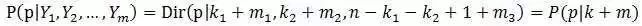
同样的，按照贝叶斯推理的逻辑，可将上述过程整理如下：

我们要猜测参数P=(p1,p2,p3)，其先验分布为Dir(p|k);

数据Yi落到三个区间[0,p1),[p1,p2],(p2,1]的个数分别是m1,m2,m3,所以m=(m1,m2,m3)服从多项分布Mult(m|p);

在给定了来自数据提供的知识m后，p的后验分布变为Dir(P|k+m)

上述贝叶斯分析过程的直观表述为：

Dir(p|k) + Multcount(m) = Dir(p|k+m)

针对于这种观测到的数据符合多项分布，参数的先验分布和后验分布都是Dirichlet分布的情况，就是Dirichlet-Multinomial共轭。这意味着，如果我们为多项分布的参数p选取的先验分布是Dirichlet分布，那么以p为参数的多项分布用贝叶斯估计得到的后验分布仍然服从Dirichlet分布。

1.7 Beta和Dirichlet分布的一个性质

如果p=Beta(t|alpha,beta)，那么

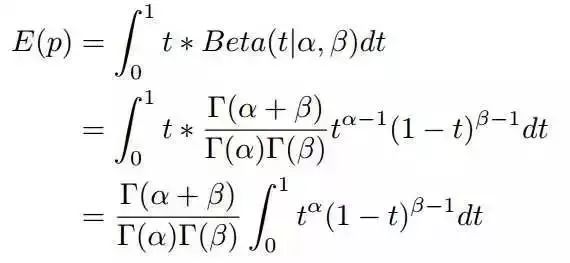
上式右边的积分对应到概率分布Beta(t|alpha+1,beta)，对于这个分布，我们有:

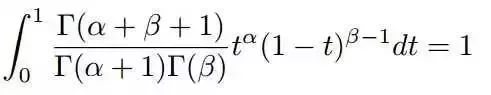
把上式带人E(p)的计算式，可以得到：

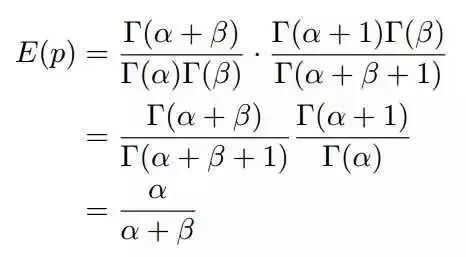
这说明，对于Beta分布的随机变量，其期望可以用上式来估计。Dirichlet分布也有类似的结论。对于p=Dir(t|alpha)，有

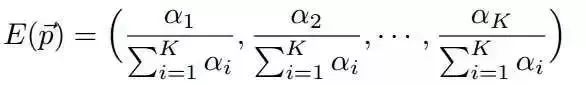
这个结论在后文的推导中会用到。

1.8 总结

LDA涉及的数学知识较多，需要认真体会，以上大部分的知识来源于文献【1,2,3】,如有不清楚的地方，参见这些文献以了解更多。

主题模型LDA

在介绍LDA之前，我们先介绍几个基础模型：Unigram model、mixture of unigrams model、pLSA model。为了方便描述，首先定义一些变量：

1 w表示词，V表示所有词的个数

2 z表示主题，k表示主题的个数

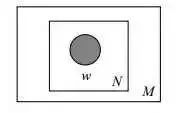
2.1 一元模型(Unigram model)

其图模型为（图中被涂色的w表示可观测变量，N表示一篇文档中总共N个单词，M表示M篇文档）：

2.2 混合一元模型(Mixture of unigrams model)

该模型的生成过程是：给某个文档先选择一个主题Z，再根据该主题生成文档，该文档中的所有词都来自一个主题。生成文档的概率为：

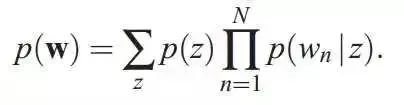
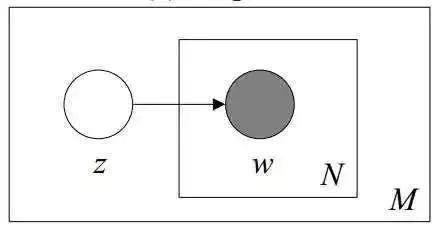
其图模型为（图中被涂色的w表示可观测变量，未被涂色的z表示未知的隐变量，N表示一篇文档中总共N个单词，M表示M篇文档）：

2.3 pLSA模型

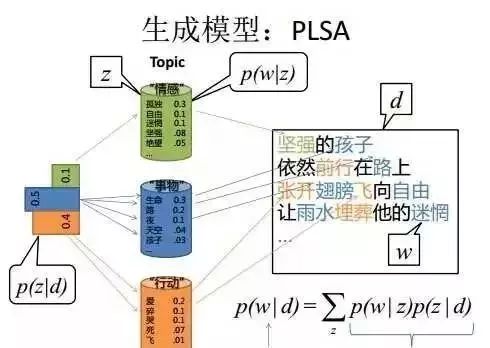
在混合一元模型中，假定一篇文档只由一个主题生成，可实际中，一篇文章往往有多个主题，只是这多个主题各自在文档中出现的概率大小不一样。在pLSA中，假设文档由多个主题生成。下面通过一个投色子的游戏（取自文献【2】的例子）说明pLSA生成文档的过程。

首先，假定你一共有K个可选的主题，有V个可选的词。假设你每写一篇文档会制作一颗K面的“文档-主题”骰子（扔此骰子能得到K个主题中的任意一个），和K个V面的“主题-词项”骰子（每个骰子对应一个主题，K个骰子对应之前的K个主题，且骰子的每一面对应要选择的词项，V个面对应着V个可选的词）。比如可令K=3，即制作1个含有3个主题的“文档-主题”骰子，这3个主题可以是：教育、经济、交通。然后令V = 3，制作3个有着3面的“主题-词项”骰子，其中，教育主题骰子的3个面上的词可以是：大学、老师、课程，经济主题骰子的3个面上的词可以是：市场、企业、金融，交通主题骰子的3个面上的词可以是：高铁、汽车、飞机。

其次，每写一个词，先扔该“文档-主题”骰子选择主题，得到主题的结果后，使用和主题结果对应的那颗“主题-词项”骰子，扔该骰子选择要写的词。先扔“文档-主题”的骰子，假设以一定的概率得到的主题是：教育，所以下一步便是扔教育主题筛子，以一定的概率得到教育主题筛子对应的某个词大学。

上面这个投骰子产生词的过程简化一下便是：“先以一定的概率选取主题，再以一定的概率选取词”。事实上，一开始可供选择的主题有3个：教育、经济、交通，那为何偏偏选取教育这个主题呢？其实是随机选取的，只是这个随机遵循一定的概率分布。比如可能选取教育主题的概率是0.5，选取经济主题的概率是0.3，选取交通主题的概率是0.2，那么这3个主题的概率分布便是{教育：0.5，经济：0.3，交通：0.2}，我们把各个主题z在文档d中出现的概率分布称之为主题分布，且是一个多项分布。

同样的，从主题分布中随机抽取出教育主题后，依然面对着3个词：大学、老师、课程，这3个词都可能被选中，但它们被选中的概率也是不一样的。比如大学这个词被选中的概率是0.5，老师这个词被选中的概率是0.3，课程被选中的概率是0.2，那么这3个词的概率分布便是{大学：0.5，老师：0.3，课程：0.2}，我们把各个词语w在主题z下出现的概率分布称之为词分布，这个词分布也是一个多项分布。

所以，选主题和选词都是两个随机的过程，先从主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该主题对应的词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。

最后，你不停的重复扔“文档-主题”骰子和”主题-词项“骰子，重复N次（产生N个词），完成一篇文档，重复这产生一篇文档的方法M次，则完成M篇文档。

上述过程抽象出来即是pLSA的文档生成模型。在这个过程中，我们并未关注词和词之间的出现顺序，所以pLSA是一种词袋模型。定义如下变量:

表示隐藏的主题；

表示海量文档中某篇文档被选中的概率；

表示词在文档中出现的概率；针对海量文档，对所有文档进行分词后，得到一个词汇列表，这样每篇文档就是一个词语的集合。对于每个词语，用它在文档中出现的次数除以文档中词语总的数目便是它在文档中出现的概率；

表示主题在文档中出现的概率；

表示词在主题中出现的概率。与主题关系越密切的词其条件概率越大。

我们可以按照如下的步骤得到“文档-词项”的生成模型：

1 按照选择一篇文档；

2 选定文档之后，从主题分布中按照概率选择主题；

3 选定主题后，从词分布中按照概率选择一个词。

利用看到的文档推断其隐藏的主题（分布）的过程，就是主题建模的目的：自动地发现文档集中的主题（分布）。文档d和单词w是可被观察到的，但主题z却是隐藏的。如下图所示（图中被涂色的d、w表示可观测变量，未被涂色的z表示未知的隐变量，N表示一篇文档中总共N个单词，M表示M篇文档）。

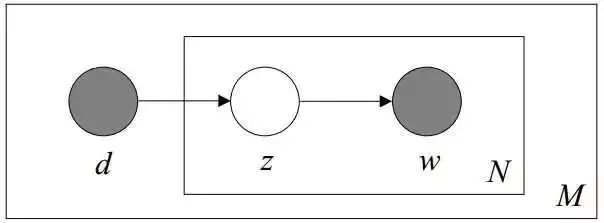
上图中，文档d和词w是我们得到的样本，可观测得到，所以对于任意一篇文档，其是已知的。根据这个概率可以训练得到文档-主题概率以及主题-词项概率。即：

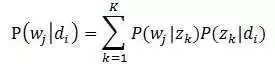
故得到文档中每个词的生成概率为：

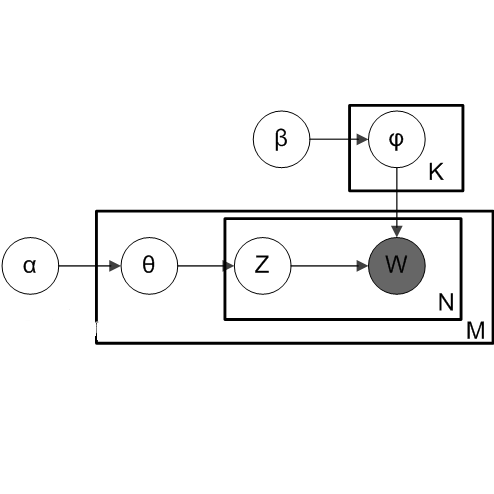
2.4 LDA模型

LDA的不同之处在于，pLSA的主题的概率分布P(c|d)是一个确定的概率分布，也就是虽然主题c不确定，但是c符合的概率分布是确定的，比如符合某个多项分布，这个多项分布的各参数是确定的。但是在LDA中，这个多项分布都是不确定的，高斯分布又服从一个狄利克雷先验分布(Dirichlet prior)。即LDA就是pLSA的贝叶斯版本,正因为LDA被贝叶斯化了，所以才会加的两个先验参数。

LDA模型中一篇文档生成的方式如下所示:

从上面的过程可以看出，LDA在pLSA的基础上，为主题分布和词分布分别加了两个Dirichlet先验。

拿之前讲解pLSA的例子进行具体说明。如前所述，在pLSA中，选主题和选词都是两个随机的过程，先从主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该主题对应的词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。在LDA中，选主题和选词依然都是两个随机的过程。但在LDA中，主题分布和词分布不再唯一确定不变，即无法确切给出。例如主题分布可能是{教育：0.5，经济：0.3，交通：0.2}，也可能是{教育：0.6，经济：0.2，交通：0.2}，到底是哪个我们不能确定，因为它是随机的可变化的。但再怎么变化，也依然服从一定的分布，主题分布和词分布由Dirichlet先验确定。

举个文档d产生主题z的例子。

在pLSA中，给定一篇文档d，主题分布是一定的，比如{ P(zi|d), i = 1,2,3 }可能就是{0.4,0.5,0.1}，表示z1、z2、z3这3个主题被文档d选中的概率都是个固定的值：P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1，如下图所示:

在LDA中，主题分布（各个主题在文档中出现的概率分布）和词分布（各个词语在某个主题下出现的概率分布）是唯一确定的。LDA为提供了两个Dirichlet先验参数，Dirichlet先验为某篇文档随机抽取出主题分布和词分布。

给定一篇文档d，现在有多个主题z1、z2、z3，它们的主题分布{ P(zi|d), i = 1,2,3 }可能是{0.4,0.5,0.1}，也可能是{0.2,0.2,0.6}，即这些主题被d选中的概率都不再是确定的值，可能是P(z1|d) = 0.4、P(z2|d) = 0.5、P(z3|d) = 0.1，也有可能是P(z1|d) = 0.2、P(z2|d) = 0.2、P(z3|d) = 0.6，而主题分布到底是哪个取值集合我们不确定，但其先验分布是dirichlet分布，所以可以从无穷多个主题分布中按照dirichlet先验随机抽取出某个主题分布出来。如下图所示