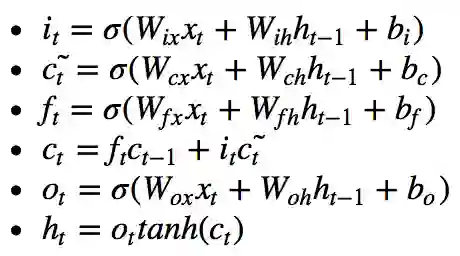【年度系列】使用LSTM预测股票市场基于Tensorflow
本期作者:Thushan Ganegedara
本期编辑:1+1=3
近 期 文 章 预 告
01、【年度系列】预测股市比你理解中的更加容易
03、【年度系列】MICI因子模型、风险模型解读系列
04、【年度系列】使用LSTM预测股票市场基于Tensorflow
05、【年度系列】如何使用LSTM预测金融时序是有效的
06、【年度系列】解析预测财务和经济时间序列的神经网络
07、【年度系列】金融领域中白箱AI
08、【年度系列】如何训练机器学会“低买高卖”
09、【年度系列】深度Q空间神经网络交易解析
10、【年度系列】深度解析均值回归交系列易1—4
13、【机器学习】使用递归神经网络(RNN)预测时序Values
14、【华尔街量化金融面试Q&A系列】第四——十期
前言
在本文开始前,作者并没有提倡LSTM是一种高度可靠的模型,它可以很好地利用股票数据中的内在模式,或者可以在没有任何人参与的情况下使用。写这篇文章,纯粹是出于对机器学习的热爱。在我看来,该模型已经观察到了数据中的某些模式,因此它可以在大多数时候正确预测股票的走势。但是,这个模型是否可以用于实际,有待用更多回测和实践去验证。
为什么需要时间序列模型?
你想要正确地模拟股票价格,因此作为股票买家,你可以合理地决定什么时候买股票,什么时候卖股票。这就是时间序列建模的切入点。你需要良好的机器学习模型,可以查看数据序列的历史记录,并正确地预测序列的未来元素是什么。
提示:股市价格高度不可预测且不稳定。这意味着在数据中没有一致的模式可以让你近乎完美地模拟股票价格。就像普林斯顿大学经济学家Burton Malkiel在他1973年的书中写到的:“随机漫步华尔街”,如果市场确实是有效的,那么当股票价格反应的所有因素一旦被公开时,那我们闭着眼睛都可以做的和专业投资者一样好。
但是,我们不要一直相信这只是一个随机过程,觉得机器学习是没有希望的。你不需要预测未来的股票确切的价格,而是股票价格的变动。做到这点就很不错了!
数据准备
使用以下数据源:
地址:https://www.kaggle.com/borismarjanovic/price-volume-data-for-all-us-stocks-etfs
当然你也可基于Wind数据库去研究。因为Wind数据相对于其他平台和数据商而言,总体上在国内算是比较全面和准确的。
从Kaggle获得数据
在Kaggle上找到的数据是csv文件,所以,你不需要再进行任何的预处理,因此你可以直接将数据加载到DataFrame中。同时你还应该确保数据是按日期排序的,因为数据的顺序在时间序列建模中至关重要。
df = df.sort_values('Date')
df.head()数据可视化
plt.figure(figsize = (18,9))
plt.plot(range(df.shape[0]),(df['Low']+df['High'])/2.0)
plt.xticks(range(0,df.shape[0],500),df['Date'].loc[::500],rotation=45)
plt.xlabel('Date',fontsize=18)
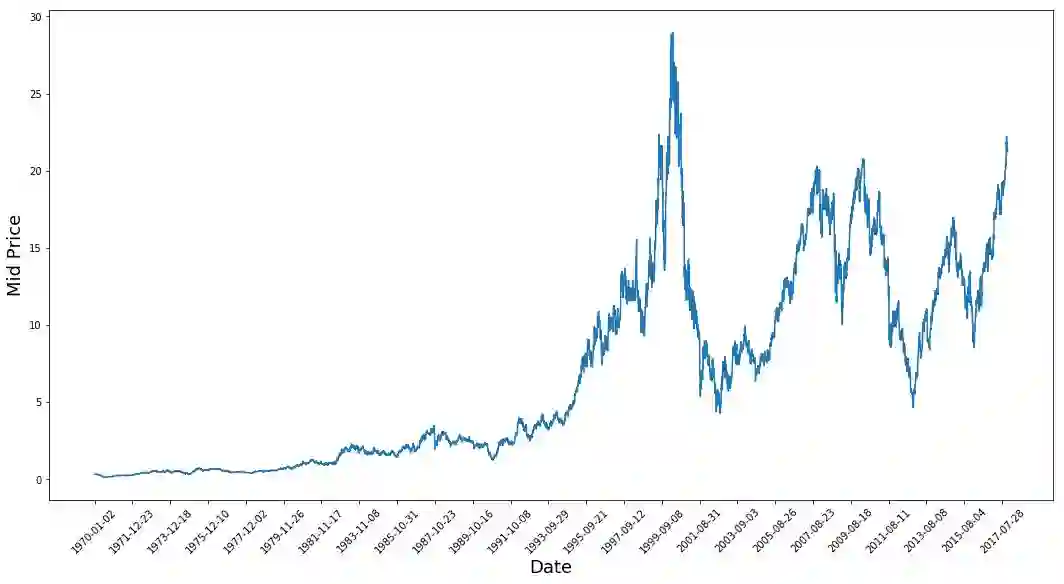
plt.ylabel('Mid Price',fontsize=18)
plt.show()上图已经说明了很多东西。我选择这家公司而不是其他公司的具体原因是,随着时间的推移,这张图中展现了不同的股价行为。这将使学习更加稳健,并且可以更改以便测试各种情况下预测的好坏程度。
数据拆分训练集和测试集
计算一天中最高和最低价的平均值来计算的中间价格。
high_prices = df.loc[:,'High'].as_matrix()
low_prices = df.loc[:,'Low'].as_matrix()
mid_prices = (high_prices+low_prices)/2.0现在你可以分离训练数据和测试数据。训练数据是时间序列的前11000个数据,其余的是测试数据。
train_data = mid_prices[:11000]
test_data = mid_prices[11000:]现在需要定义一个标准对数据进行归一化。MinMaxScalar方法将所有数据归到0和1之间。你还可以将训练和测试数据重新组为[data_size, num_features]。
scaler = MinMaxScaler()
train_data = train_data.reshape(-1,1)
test_data = test_data.reshape(-1,1)根据之前得数据,可以看出不同时间段有不同的取值范围,你可以将整个序列拆分为窗口来进行归一化。如果不这样做,早期的数据接近于0,并且不会给学习过程增加太多价值。这里你选择的窗口大小是2500。
当选择窗口大小时,确保它不是太小,因为当执行窗口规范化时,它会在每个窗口的末尾引入一个中断,因为每个窗口都是独立规范化的。
在本例中,4个数据点将受此影响。但假设你有11000个数据点,4个点不会引起任何问题。
smoothing_window_size = 2500
for di in range(0,10000,smoothing_window_size):
scaler.fit(train_data[di:di+smoothing_window_size,:])
train_data[di:di+smoothing_window_size,:] = scaler.transform(train_data[di:di+smoothing_window_size,:])
# You normalize the last bit of remaining data
scaler.fit(train_data[di+smoothing_window_size:,:])
train_data[di+smoothing_window_size:,:] = scaler.transform(train_data[di+smoothing_window_size:,:])将数据重新塑造为[data_size]的Shape:
train_data = train_data.reshape(-1)
test_data = scaler.transform(test_data).reshape(-1)现在可以使用指数移动平均平滑数据。可以帮助你避免股票价格数据的杂乱,并产生更平滑的曲线。
我们只使用训练数据来训练MinMaxScaler,通过将MinMaxScaler与测试数据进行匹配来规范化测试数据是错误的。
注意:你应该只平滑训练数据。
EMA = 0.0
gamma = 0.1
for ti in range(11000):
EMA = gamma*train_data[ti] + (1-gamma)*EMA
train_data[ti] = EMA
all_mid_data = np.concatenate([train_data,test_data],axis=0)下面是平均结果。它非常接近股票的实际行为。接下来您将看到一个更精确的一步预测方法:
上面的图(和MSE)说明了什么呢?对于非常短的predictiosn(一天之后)来说,这个模型似乎不算太坏。考虑到股票价格在一夜之间不会从0变化到100,这种行为是明智的。接下来我们来看一种更有趣的平均技术,称为指数移动平均。
指数移动平均线
你可能在互联网上看到过一些文章使用非常复杂的模型来预测股票市场的行为。但是要小心!我所看到的这些都只是视觉错觉,不是因为学习了有用的东西。下面你将看到如何使用简单的平均方法复制这种行为。
window_size = 100
N = train_data.size
run_avg_predictions = []
run_avg_x = []
mse_errors = []
running_mean = 0.0
run_avg_predictions.append(running_mean)
decay = 0.5
for pred_idx in range(1,N):
running_mean = running_mean*decay + (1.0-decay)*train_data[pred_idx-1]
run_avg_predictions.append(running_mean)
mse_errors.append((run_avg_predictions[-1]-train_data[pred_idx])**2)
run_avg_x.append(date)
print('MSE error for EMA averaging: %.5f'%(0.5*np.mean(mse_errors)))
MSE error for EMA averaging: 0.00003
如果指数移动平均线很好,为什么需要更好的模型呢?
可以看到,它符合遵循真实分布的完美直线(通过非常低的MSE证明了这一点)。实际上,仅凭第二天的股票市值,你就做不了什么。就我个人而言,我想要的不是第二天股市的确切价格,而是未来30天股市的价格会上涨还是下跌
让我们试着在窗口中进行预测(假设你预测接下来两天的窗口,而不是第二天)。然后你就会意识到EMA会有多么的失败。让我们通过一个例子来理解这一点。
不管你预测未来的步骤是多少,你都会得到相同的答案。
输出有用信息的一种解决方案是查看基于动量算法。他们的预测是基于过去的近期值是上升还是下降(而不是精确的数值)。例如,如果过去几天的价格一直在下降,第二天的价格可能会更低。这听起来很合理。然而,我们将使用更复杂的模型:LSTM。
评价结果
我们将使用均值平方误差来计算我们的模型有多好。均值平方误差(MSE)的计算方法是先计算真实值与预测值之间的平方误差,然后对所有的预测进行平均。但是:
平均预测是一种很好的预测方法(这对股票市场的预测不是很有用),但对未来的预测并不是很有用。
LSTM简介
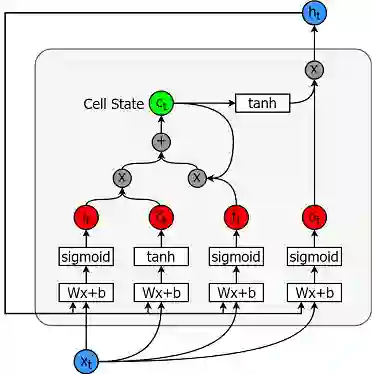
长短时记忆模型是非常强大的时间序列模型。它们可以预测未来任意数量的步骤。LSTM模块(或单元)有5个基本组件,可以对长期和短期数据进行建模。
LSTM单元格如下所示:
计算方程如下:
Tensorflow为实现时间序列模型提供了一个很好的子API。后面我们会使用到它。
LSTM数据生成器
首先要实现一个数据生成器来训练LSTM。这个数据生成器将有一个名为unroll_batch(…)的方法,该方法将输出一组按顺序批量获取num_unrollings的输入数据,其中批数据的大小为[batch_size, 1]。然后每批输入数据都有相应的输出数据。
例如,如果num_unrollings=3和batch_size=4则看起来像一组展开的批次。
输入数据: [x0,x10,x20,x30],[x1,x11,x21,x31],[x2,x12,x22,x32]
输出数据: [x1,x11,x21,x31],[x2,x12,x22,x32],[x3,x13,x23,x33]
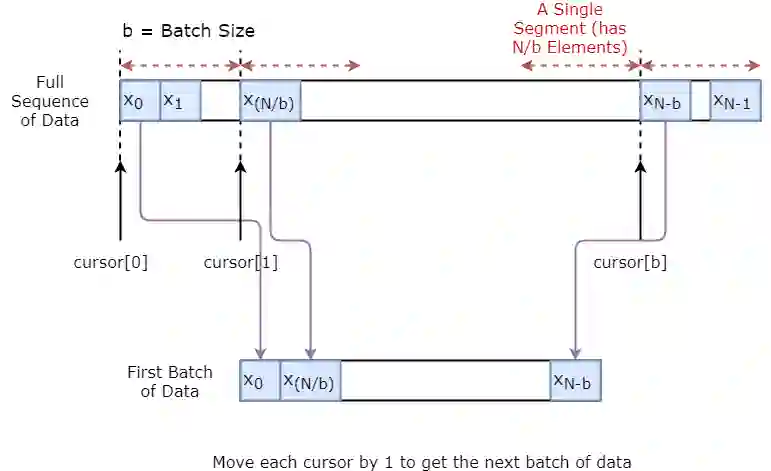
数据生成器
下面将演示如何可视化创建一批数据。基本思想是将数据序列划分为N / b段,使每个段的大小为b,然后定义游标每段为1。然后对单个数据进行抽样,我们得到一个输入(当前段游标索引)和一个真实预测(在[当前段游标+1,当前段游标+5]之间随机抽样)。请注意,我们并不总是得到输入旁边的值,就像它的预测一样。这是一个减少过拟合的步骤。在每次抽样结束时,我们将光标增加1。
定义超参数
在本节中,将定义几个超参数。D是输入的维数。很简单,你以之前的股票价格作为输入并预测下一个应该为1。
然后是num_unrollings,它表示单个优化步骤需要考虑多少连续时间步骤。越大越好。
然后是batch_size。批量处理大小是在单个时间步骤中考虑的数据样本的数量。越大越好,因为在给定的时间内数据的可见性越好。
接下来定义num_nodes,它表示每个单元格中隐藏的神经元数量。在这个示例中,你可以看到有三层LSTM。
D = 1
num_unrollings = 50
batch_size = 500
num_nodes = [200,200,150]
n_layers = len(num_nodes)
dropout = 0.2
tf.reset_default_graph()定义输入和输出
接下来为训练输入和标签定义占位符。这非常简单,因为你有一个输入占位符列表,其中每个占位符包含一批数据。 该列表包含num_unrollings占位符,它将用于单个优化步骤。
train_inputs, train_outputs = [],[]
for ui in range(num_unrollings):
train_inputs.append(tf.placeholder(tf.float32, shape=[batch_size,D],name='train_inputs_%d'%ui))
train_outputs.append(tf.placeholder(tf.float32, shape=[batch_size,1], name = 'train_outputs_%d'%ui))定义LSTM和回归层的参数
用三个LSTM层和一个线性回归层,用w和b表示,该层提取最后一个长短期内存单元的输出并输出对下一个时间步骤的预测。你可以使用TensorFlow中的MultiRNNCell来封装创建的三个LSTMCell对象。此外,还可以使用dropout实现LSTM单元格,因为它们可以提高性能并减少过拟合。
lstm_cells = [
tf.contrib.rnn.LSTMCell(num_units=num_nodes[li],
state_is_tuple=True,
initializer= tf.contrib.layers.xavier_initializer()
)
for li in range(n_layers)]
drop_lstm_cells = [tf.contrib.rnn.DropoutWrapper(
lstm, input_keep_prob=1.0,output_keep_prob=1.0-dropout, state_keep_prob=1.0-dropout
) for lstm in lstm_cells]
drop_multi_cell = tf.contrib.rnn.MultiRNNCell(drop_lstm_cells)
multi_cell = tf.contrib.rnn.MultiRNNCell(lstm_cells)
w = tf.get_variable('w',shape=[num_nodes[-1], 1], initializer=tf.contrib.layers.xavier_initializer())
b = tf.get_variable('b',initializer=tf.random_uniform([1],-0.1,0.1))计算LSTM输出并将其输入回归层,得到最终预测结果
首先创建TensorFlow变量(c和h),它将保持单元状态和长短期记忆单元的隐藏状态。 然后将train_input列表转换为[num_unrollings, batch_size, D],使用tf.nn.dynamic_rnn计算所需输出。然后使用tf.nn.dynamic_rnn计算LSTM输出。并将输出分解为一列num_unrolling的张量。预测和真实股价之间的损失。
c, h = [],[]
initial_state = []
for li in range(n_layers):
c.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
h.append(tf.Variable(tf.zeros([batch_size, num_nodes[li]]), trainable=False))
initial_state.append(tf.contrib.rnn.LSTMStateTuple(c[li], h[li]))
all_inputs = tf.concat([tf.expand_dims(t,0) for t in train_inputs],axis=0)
all_lstm_outputs, state = tf.nn.dynamic_rnn(
drop_multi_cell, all_inputs, initial_state=tuple(initial_state),
time_major = True, dtype=tf.float32)
all_lstm_outputs = tf.reshape(all_lstm_outputs, [batch_size*num_unrollings,num_nodes[-1]])
all_outputs = tf.nn.xw_plus_b(all_lstm_outputs,w,b)
split_outputs = tf.split(all_outputs,num_unrollings,axis=0)损失计算和优化器
现在,要计算损失。然而,在计算损失时,你应该注意到有一个独特的特征。对于每一批预测和真实输出,计算均方误差。然后把所有这些均方损失加起来(不是平均值)。最后,定义要用来优化神经网络的优化器在这种情况下,您可以使用Adam,这是一个非常新且性能良好的优化器。
print('Defining training Loss')
loss = 0.0
with tf.control_dependencies([tf.assign(c[li], state[li][0]) for li in range(n_layers)]+
[tf.assign(h[li], state[li][1]) for li in range(n_layers)]):
for ui in range(num_unrollings):
loss += tf.reduce_mean(0.5*(split_outputs[ui]-train_outputs[ui])**2)
print('Learning rate decay operations')
global_step = tf.Variable(0, trainable=False)
inc_gstep = tf.assign(global_step,global_step + 1)
tf_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
tf_min_learning_rate = tf.placeholder(shape=None,dtype=tf.float32)
learning_rate = tf.maximum(
tf.train.exponential_decay(tf_learning_rate, global_step, decay_steps=1, decay_rate=0.5, staircase=True),
tf_min_learning_rate)
# Optimizer.
print('TF Optimization operations')
optimizer = tf.train.AdamOptimizer(learning_rate)
gradients, v = zip(*optimizer.compute_gradients(loss))
gradients, _ = tf.clip_by_global_norm(gradients, 5.0)
optimizer = optimizer.apply_gradients(
zip(gradients, v))
print('\tAll done')这里定义了与预测相关的TensorFlow操作。首先,为输入(sample_inputs)定义一个占位符,然后与训练阶段类似,定义预测的状态变量(sample_c和sample_h)。最后用tf.nn.dynamic_rnn计算预测。后通过回归层(w和b)发送输出。 还应该定义reset_sample_state操作,该操作将重置单元状态和隐藏状态。 每次进行一系列预测时,都应该在开始时执行此操作。
print('Defining prediction related TF functions')
sample_inputs = tf.placeholder(tf.float32, shape=[1,D])
sample_c, sample_h, initial_sample_state = [],[],[]
for li in range(n_layers):
sample_c.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
sample_h.append(tf.Variable(tf.zeros([1, num_nodes[li]]), trainable=False))
initial_sample_state.append(tf.contrib.rnn.LSTMStateTuple(sample_c[li],sample_h[li]))
reset_sample_states = tf.group(*[tf.assign(sample_c[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)],
*[tf.assign(sample_h[li],tf.zeros([1, num_nodes[li]])) for li in range(n_layers)])
sample_outputs, sample_state = tf.nn.dynamic_rnn(multi_cell, tf.expand_dims(sample_inputs,0),
initial_state=tuple(initial_sample_state),
time_major = True,
dtype=tf.float32)
with tf.control_dependencies([tf.assign(sample_c[li],sample_state[li][0]) for li in range(n_layers)]+
[tf.assign(sample_h[li],sample_state[li][1]) for li in range(n_layers)]):
sample_prediction = tf.nn.xw_plus_b(tf.reshape(sample_outputs,[1,-1]), w, b)
print('\tAll done')运行LSTM
在这里,你将训练和预测几个时期的股票价格走势,看看这些预测是否会随着时间的推移而变得更好或更糟。按照以下步骤操作:
在时间序列上定义一组测试起点(test_points_seq)来计算LSTM
对于每一个epoch
用于训练数据的完整序列长度
展开一组num_unrollings批次
使用展开的批次LSTM进行训练
计算平均训练损失
对于测试集中的每个起点
通过迭代在测试点之前找到的以前的num_unrollings数据点来更新LSTM状态
使用先前的预测作为当前输入,连续预测n_predict_once步骤
计算预测到的n_predict_once点与当时股票价格之间的MSE损失
部分代码
epochs = 30
valid_summary = 1
n_predict_once = 50
train_seq_length = train_data.size
train_mse_ot = []
test_mse_ot = []
predictions_over_time = []
session = tf.InteractiveSession()
tf.global_variables_initializer().run()
loss_nondecrease_count = 0
loss_nondecrease_threshold = 2
print('Initialized')
average_loss = 0
data_gen = DataGeneratorSeq(train_data,batch_size,num_unrollings)
x_axis_seq = []
test_points_seq = np.arange(11000,12000,50).tolist()
for ep in range(epochs):
# ========================= Training =====================================
for step in range(train_seq_length//batch_size):
u_data, u_labels = data_gen.unroll_batches()
feed_dict = {}
for ui,(dat,lbl) in enumerate(zip(u_data,u_labels)):
feed_dict[train_inputs[ui]] = dat.reshape(-1,1)
feed_dict[train_outputs[ui]] = lbl.reshape(-1,1)
feed_dict.update({tf_learning_rate: 0.0001, tf_min_learning_rate:0.000001})
_, l = session.run([optimizer, loss], feed_dict=feed_dict)可视化预测
可以看到MSE损失是如何随着训练量的减少而减少的。这是一个好迹象,表明模型正在学习一些有用的东西。你可以看到LSTM比标准平均值做得更好。标准平均(虽然不完美)合理地跟随真实的股票价格运动。
best_prediction_epoch = 28
plt.figure(figsize = (18,18))
plt.subplot(2,1,1)
plt.plot(range(df.shape[0]),all_mid_data,color='b')
predictions with high alpha
start_alpha = 0.25
alpha = np.arange(start_alpha,1.1,(1.0-start_alpha)/len(predictions_over_time[::3]))
for p_i,p in enumerate(predictions_over_time[::3]):
for xval,yval in zip(x_axis_seq,p):
plt.plot(xval,yval,color='r',alpha=alpha[p_i])
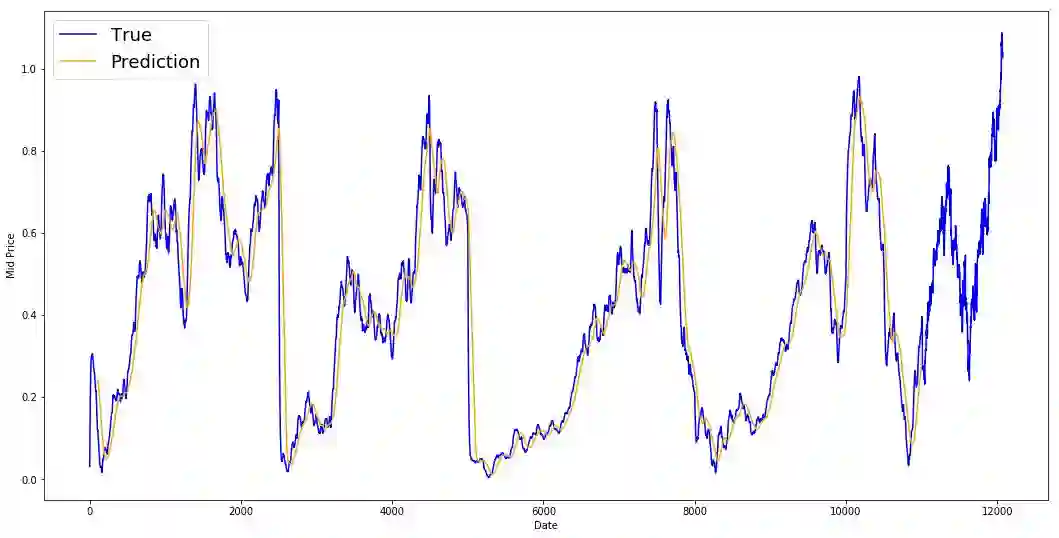
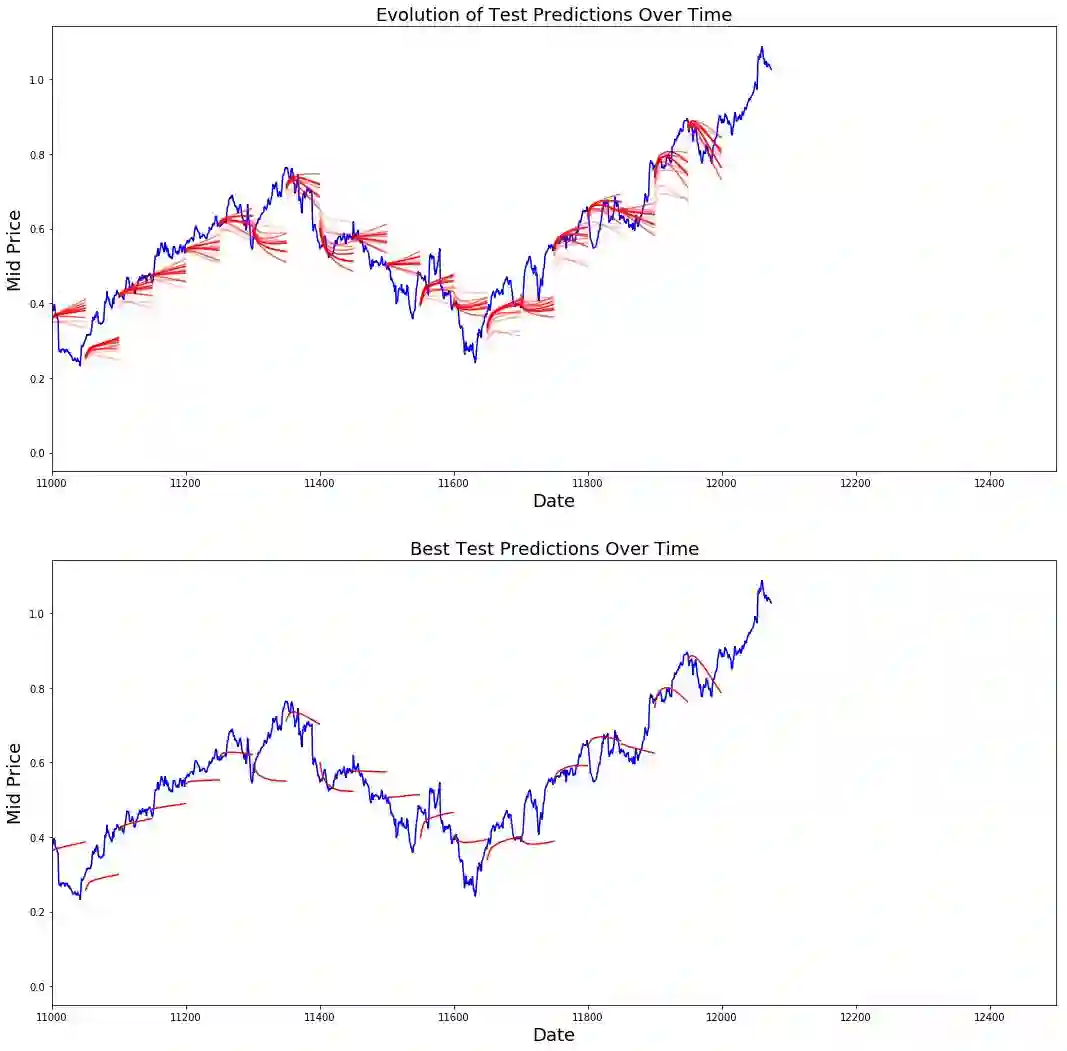
plt.title('Evolution of Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.subplot(2,1,2)
plt.plot(range(df.shape[0]),all_mid_data,color='b')
for xval,yval in zip(x_axis_seq,predictions_over_time[best_prediction_epoch]):
plt.plot(xval,yval,color='r')
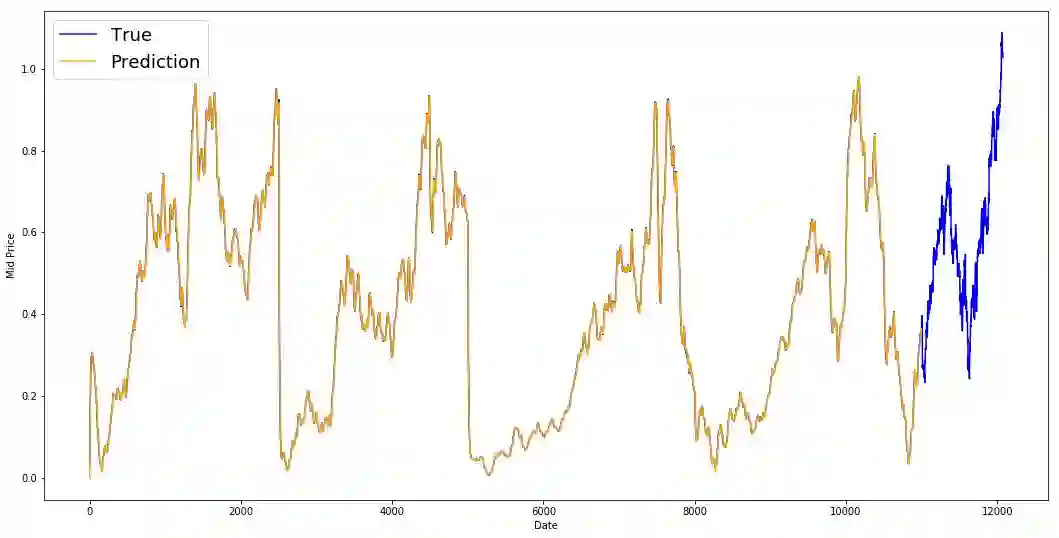
plt.title('Best Test Predictions Over Time',fontsize=18)
plt.xlabel('Date',fontsize=18)
plt.ylabel('Mid Price',fontsize=18)
plt.xlim(11000,12500)
plt.show()尽管LSTM并不完美,但它似乎在大多数情况下都能正确预测股价走势。请注意,你的预测大致在0和1之间(也就是说,不是真实的股票价格)。这是可以的,因为你预测的是股价的走势,而不是股价本身。
结论
股票价格/移动预测是一项极其困难的任务。就我个人而言,我认为任何股票预测模型都不应该被视为理所当然,并且盲目地依赖它们。然而,模型在大多数情况下可能能够正确预测股票价格的变动,但并不总是如此。
不要被那些预测曲线完全与真实股价重叠的文章所迷惑。这可以用一个简单的平均技术来复制,但实际上它是无用的。更明智的做法是预测股价走势。
模型的超参数对你得到的结果非常敏感。因此,一个非常好的事情是在超参数上运行一些超参数优化技术(例如,网格搜索/随机搜索)。这里列出了一些最关键的超参数:优化器的学习率、层数、每层的隐藏单元数,优化器Adam表现最佳,模型的类型(GRU / LSTM / LSTM with peepholes)。
由于本文由于数据量小,我们用测试损耗来衰减学习速率。这间接地将测试集的信息泄露到训练过程中。处理这个问题更好的方法是有一个单独的验证集(除了测试集)与验证集性能相关的衰减学习率。
推荐阅读
知识在于分享
在量化投资的道路上
你不是一个人在战斗