隐藏在人类身体中的数学

我们知道幼儿开始学数数的时候是用手指的，有时候也用到脚趾。这些叫做“digits”（编者注：digit，医学名词，手指脚趾），那么这个单词在十进制中用来并表示0,1,2,3,4,5,6,7,8,9这些数字也并不偶然。所以，我们的身体是我们学习算数的第一位老师。

>>>> 

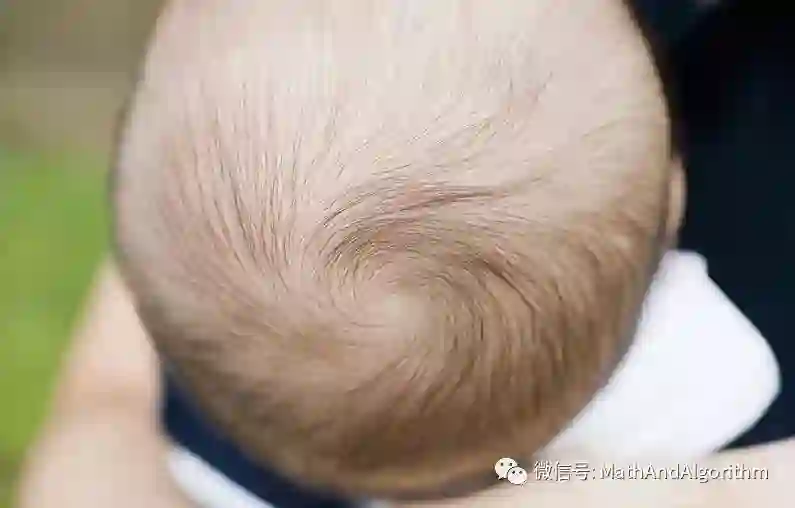
但是一个鲜为人知的事实是我们的身体也试图教我们高等的数学，只要我们希望如此。来看婴儿的第一个发式：

头发中间那个可爱的漩涡，按数学的说法，就是一个“奇点”，这个婴儿的头发似乎无法决定该往哪个方向生长的一个点。它后面的头发向左而前面的头发向右生长。在这点附近，头发有的向前有的向后。使得这个发型在该处“奇异”的是一个突然而且不连续变化的变量（这个变量就是头发的方向）。

自然界中不乏奇点，在飓风的风眼中根本没有风，然而在周围的所有和任何方向上都有风吹。同样似是而非的事情发生在北极点。如果你以刘易斯.卡罗尔(Lewis Carroll)的风格来发问，现在北极点是什么时间，那么仅有意义的回答听起来像个笑话：所有时间。所有的时区在北极点汇合，所以从这个奇点沿着不同的经线迈出去你可以到达任何你想去的时区。

奇点反映了自然界解决不匹配的尝试，克服一切困难坚持连续性。当分歧成为必然（在头发的方向或风吹的方向或时区中间），奇点尽可能的把不匹配局限在最小的范围，一个点。

奇点一个非常显著的特点是它能坚持。它们有一种持久性。随着你长大，你的头骨和头皮也越来越大，但是发式中的那个漩涡却一直在。

拓扑学是高等数学的一个分支，它就是用来处理这种经久性的特性。它经常被定义为研究形状经过连续变化之后不会改变的那些性质。为了看到这其中的含义，想象我们在一张很薄的弹性纤维上素描一个婴儿的发型。现在我们把这张纤维变形，拉伸它，弯曲它，扭曲它，但不要撕开它或者把任何部分粘在一起。你的努力歪曲了这张素描的几何结构（有些头发离得远了，有的头发之间的角度改变了），但是它的拓扑结构却未改变（发式依旧，交叉的头发依然交叉，没交叉的头发也依然不交叉）。

或者你看一下自己的手指和手掌。看到那些整齐图案的指纹隆起了吧？在皮肤的很小的部分它们是几乎是互相平行的。这又是自然界施行连续性的特点。但是当不同部分的隆起迎头撞在一起的时候，就很难让所有的都高兴了。每个隆起都想与邻居平行，但也想把新来的加入进来。碰撞产生了不可避免的不连续性--奇点--这使得看手相的人和FBI感兴趣。这就是你的皮肤教给你拓扑学的方式。

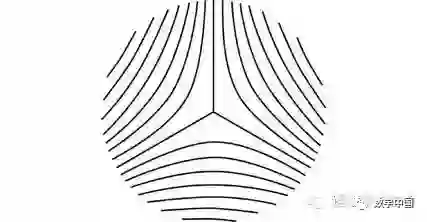
当查看你的手相时，你会注意到很少一些类型的奇点。两种最基本的奇点类型是三叉点

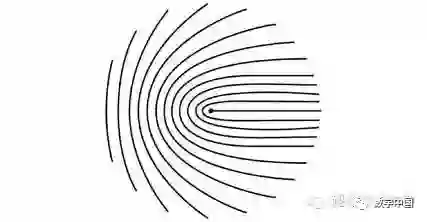
和环点

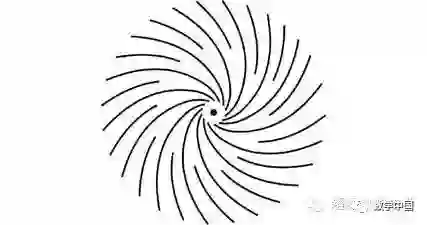
指纹上所有其他的奇点可由这两种构造出来。例如，这种叫做螺纹的奇点

可被视作两个环的融合

它们挤在了一起让两个中间的终点重合。

1965年一位英国遗传学家莱昂纳尔.彭罗斯(Lionel Penrose)指出指纹和掌纹符合一个普遍性的法则：不论你自己的纹型如何，所有五指的手上的的三叉点总比环点多4个。（他的记录中把螺纹当作两个环，原因见上述的解释。）

这里讽刺的很令人惊讶。我们炫耀的最大的区别性特征--我们指纹和掌纹的几何--也是最难区分的：同样的拓扑法则适合我们所有人。

彭罗斯把他的法则推广到出生并非五指的手上，这常常是由于遗传异常造成的。如果用D来表示一个手上的手指数目，彭罗斯的法则是三叉点的数目T减去环点的数目L等于手指的数目减去1：

T-L=D-1.

1979年彭罗斯的儿子罗杰(Roger)，一名数学物理学家，发表了一篇纪念他父亲的优美文章，在这篇文章中，他用拓扑学推导出了他父亲的法则。让我现在概述一下他的证明。

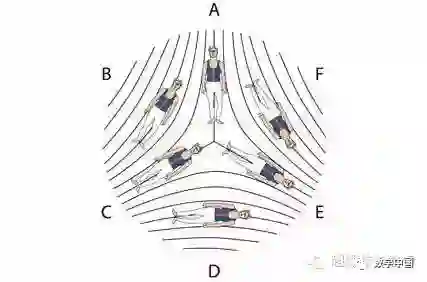
第一步是为每一种类型的奇点分配一个数字。这个数字传统上称为奇点的“指标”，这并不是有意地与手指双关。为了明白它的意义，想象一个细小的体操运动员吉姆，他逆时针绕着这个奇点环行一圈。在他行进中的每一点，吉姆都很小心地调整他的方向来保持与那里的指纹隆起的方向一致，这会导致他旋转。

这是当他在绕三叉点运动时发生的状况：

在一点处A，吉姆站立向上来保持与那里的指纹隆起一致。在一点处B，他沿顺时针方向稍微转了一下。当完成围绕三叉点一整圈，他现在头部向下，与他开始时颠倒了过来，相当于他做了一个180度顺时针旋转，与他的绕行的逆时针方向相反。

一般的，一个奇点的指标衡量吉姆沿逆时针方向绕奇点一周时完成的180度旋转的净数；用正负号来表示逆时针旋转（+）或顺时针旋转（-）。所以这种类型的奇点的指标是-1。

然而逆时针绕行一个环奇点会让吉姆逆时针旋转180度。也就是说环奇点的指标是+1。

下一步的论证要用到关于指标的一个重要事实：如果吉姆绕着包含2个或更多奇点绕行一周的话，这些奇点的指标之和就预示了他会旋转多少个180度。相反地，他绕行一圈后旋转的180度的净数等于他绕行路径内部的奇点的指标之和。这组声明称为指标定理。它如下地暗示了彭罗斯法则。

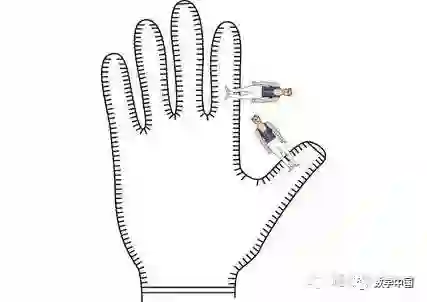
让吉姆绕着整个扁平的手掌一圈：、

由日常的经验我们知道手掌和手指的纹路隆起表现如图所示——趋于与指尖和手腕平行，并在手指和手掌边缘指向外侧。所以当吉姆逆时针绕着扁平的手部一圈，他只在手指缝隙间翻动。五指的人有4个手指缝隙。在每个缝隙中，吉姆顺时针旋转180度。所以吉姆旋转的180度的净数是-4，由指标定理，这必然等于内部的所有奇点指标之和。因为三叉点的指标是-1，环点的指标是+1，那么三叉点的个数一定比环点的个数多4，这正是关于五指手的彭罗斯法则。

沿用罗杰.彭罗斯的做法，我以本文纪念我的导师，Art Winfree，世界上最伟大的数学生物学家之一。他的很多工作是关于我们身体和大脑生物钟奇点的。

用以上的拓扑学推理，Art预测心跳的节律到睡眠的周期有它们自己的北极点，在那里心律的相(phase)变得奇异，睡眠周期会终止。他的这一想法被实验证实，现在被医生和试图揭开心律失常的生物研究人员视为一条重要的线索。

尽管元凶依然在逃，但我们已有有希望的线索。就像Art喜欢引用的夏洛克·福尔摩斯的那句话“奇特总能提供一些线索”（Singularity is almost invariably a clue）。

注记

1.一个关于拓扑学包含指标定理的活泼生动易于理解的介绍请看：D. Richeson, “Euler’s Gem”(Princeton University Press, 2008).

2.基于他的临床观察，彭罗斯是第一个分析指纹和掌纹的纹型的，请看:L. S. Penrose, “Dermatoglyphic topology,” Nature, Vol. 205(1965), pp. 544–546.这篇文章陈述的法则现在名为彭罗斯法则。

关于罗杰.彭罗斯对于他父亲的法则的拓扑学证明，请看:R. Penrose, “The topology of ridge systems,” Annals of Human Genetics, Vol. 42(1979), pp. 435–444. 我对于这个题目的处理以及文中环点、螺纹以及三叉点的图片，均受到这篇优美文章的启发。

另外一个独立的分析，能得到同样结论并推广到纤维细胞的培养（一种结缔组织中的细胞），请看：Elsdsale and F. Wasoff, “Fibroblast cultures and dermatoglyphics: The topology of two planar patterns,” Wilhelm Roux’s Archives of Developmental Biology, Vol. 180(1976), pp. 121–147.

3.关于指纹历史以及在犯罪调查中的应用，请看：S. A. Cole, “Suspect Identities”(Harvard University Press, 2002)以及C. Beavan, “Fingerprints”(Hyperion, 2002).

4.当你查看自己的手的时候，你或许不会有任何问题就能看清你的指纹，但是你或许需要明亮的光线和放大镜才能看清纹路隆起经过你的手指下方延续到手掌。在老年人或者从事重体力活的体力劳动者，如砖瓦工，这些纹路很难看清，就像轮胎磨损面。

5.Art Winfree关于生物节律中的相奇点和他他其他的一些工作，请看他的巨著：“The Geometry of Biological Time,” 2nd edition(Springer, 2001).很多人发现这本书由于它的特色很难读，但这是本很棒的书，值得一试。Winfree早期的、或许更容易读的关于奇点如何牵涉到心律失常的描述，请看：A. T. Winfree, “Sudden cardiac death: a problem in topology?” Scientific American, Vol. 248, No. 5(1983), pp. 144–161,以及“When Time Breaks Down”(Princeton University Press, 1987).

6.“奇特总能提供一些线索”。（Singularity is almost invariably a clue）：引用自柯南.道尔“福尔摩斯历险记”中的“博斯科姆比溪谷秘案”（The Boscombe Valley Mystery ）。

∑编辑 | Gemini

来源 | 善科文库