机器学习算法的运算基础——矩阵

课程介绍

机器学习是一门集概率论、线性代数、数值计算、最优化理论和计算机科学等多个领域的交叉学科。本门课程——即《机器学习之矩阵》囊括了机器学习理论中所需要的和线性代数相关的所有知识。 主要包括矩阵的定义、性质、运算、分解以及应用。另外，还会讲解线性空间、范数、生成子空间相关知识。

主题：《机器学习之矩阵》

讲师：黄博士

开课时间：8月5日起，每周六、日上午10:00-12:00在线直播

报名：戳“阅读原文”或扫描下方课程二维码。

活动：转发朋友圈，即可获得50元优惠券，低至249元！

《机器学习之矩阵》

讲师介绍

黄博士：浙江大学应用数学系博士，现任教于浙江师范大学，专业从事公共课数学教学，包括线性代数、高等数学等学科。

开课时间：8月5日起，每周六、日上午10:00-12:00 在线直播

课程特色

本课程由专业数学系老师讲解，从数学背景和现实应用中讲解线性代数的相关知识，摆脱传统的讲概念、记公式、解体的数学学习模式，让听众对线性代数有一个全新的、深刻的认识。

课程大纲

第一课：矩阵初步

1. 矩阵的基本概念：

（1）实数、向量、矩阵、张量

（2）矩阵和向量的关系

（3）矩阵和方程组的关系

（4）特殊矩阵：单位矩阵，数量矩阵，对角矩阵，三角矩阵 

2. 矩阵的基本运算：

（1）矩阵的加、减、乘（数乘和矩阵乘法）、除，转置（对称矩阵），求行列式

（2）方程组的矩阵表示

（3）矩阵三个初等变换

（4）矩阵的逆、秩、迹

第二课：矩阵变换和线性空间

1. 线性空间

（1）线性的概念、线性相关、线性表示（线性组合）和方程组的关系

（2）线性空间、线性子空间（生成子空间）、向量组的值域和核

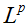
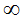
（3）线性空间的范数、范数（p=1、2、）、矩阵的Frobenius范数

2. 矩阵分解

（1）特征分解、正交分解、正定（半正定）矩阵、正定矩阵和特征分解之间的关系、SVD分解（Moore-Penrose伪逆）

（2）应用举例：PCA

第三课：矩阵求导

1. 梯度向量、Hessin矩阵、方向导数、多元函数泰勒展开、梯度下降

2. 应用举例：最小二乘法

面向人群

1. 零基础，想入门机器学习；

2. 想深入研究机器学习；

3. 想补充数学基础知识的相关从业人员；

4. 对机器学习（尤其是竞赛）感兴趣的在校学生或从业人员。

咨询&报名

矩阵还不过瘾？数学基础都需要补？我们还有《机器学习之概率与统计推断》、《机器学习之凸优化》哦！戳链接课程 | 这才是补数学基础的正确姿势可报名《机器学习之数学基础》系列课程~~！

扫课程二维码直接报名《机器学习之矩阵》！

加课程小助手回复“722”进群咨询

付款后加小助手进课程群