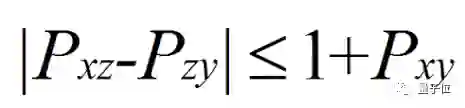证明爱因斯坦错了！诺贝尔物理学奖今年颁给量子纠缠，潘建伟博士导师加冕

来源：量子位
  本文为约2402字，建议阅读5分钟
本文介绍了三位2022年诺贝尔物理学奖得主以及他们的主要科研成果。

2022年诺贝尔物理学奖揭晓了！

今年的物理学奖颁向量子纠缠的三位科学家，他们分别是阿兰·阿斯佩Alain Aspect，约翰·克劳泽John F. Clauser以及安东·塞林格Anton Zeilinger，以表彰他们用纠缠光子进行实验，证明了贝尔不等式不成立，并以此开创量子信息科学。

换言之，他们成功证明了爱因斯坦是错的。

他们三人将共享1000万瑞典克朗的奖金。值得一提的是，其中塞林格还是潘建伟院士的博士导师。

证明了爱因斯坦是错的

官方评价中提到，他们的实验为当下量子技术革命奠定了基础，真正推动量子力学从理论走向了应用。

这其中最关键的贡献就是用量子纠缠实验，证明了贝尔不等式不成立。

量子纠缠，就是在两个分隔的粒子或者多个粒子，在彼此相互作用时，由于各个粒子所拥有的特性已综合成为整体性质，无法单独描述各个粒子的性质。

图源：© Johan Jarnestad/瑞典皇家科学院

最早在1935年，就有人发现了这一现象，其中就包括爱因斯坦。薛定谔也发表了几篇相关论文，还定下了量子纠缠这一术语。

但这种行为被爱因斯坦抨击为违背定域实在论，并讥讽量子纠缠为“鬼魅般的超距作用”（spooky action at a distance）还曾说：“我相信上帝不掷骰子。他表示，量子力学的标准表述不具完备性。

上世纪60年代，贝尔提出论文表明，对于爱因斯坦的定域实在论本身存在矛盾，相反量子力学得到的关联结果要强很多。与此同时，还提出了贝尔不等式，将这种差别定性。

在经典力学中，这个不等式成立，而在量子力学中这个不等式就不成立。它可以应用于任何由两个相互纠缠的粒子所组成的量子系统。最常见的范例是纠缠于自旋或偏振的粒子系统。

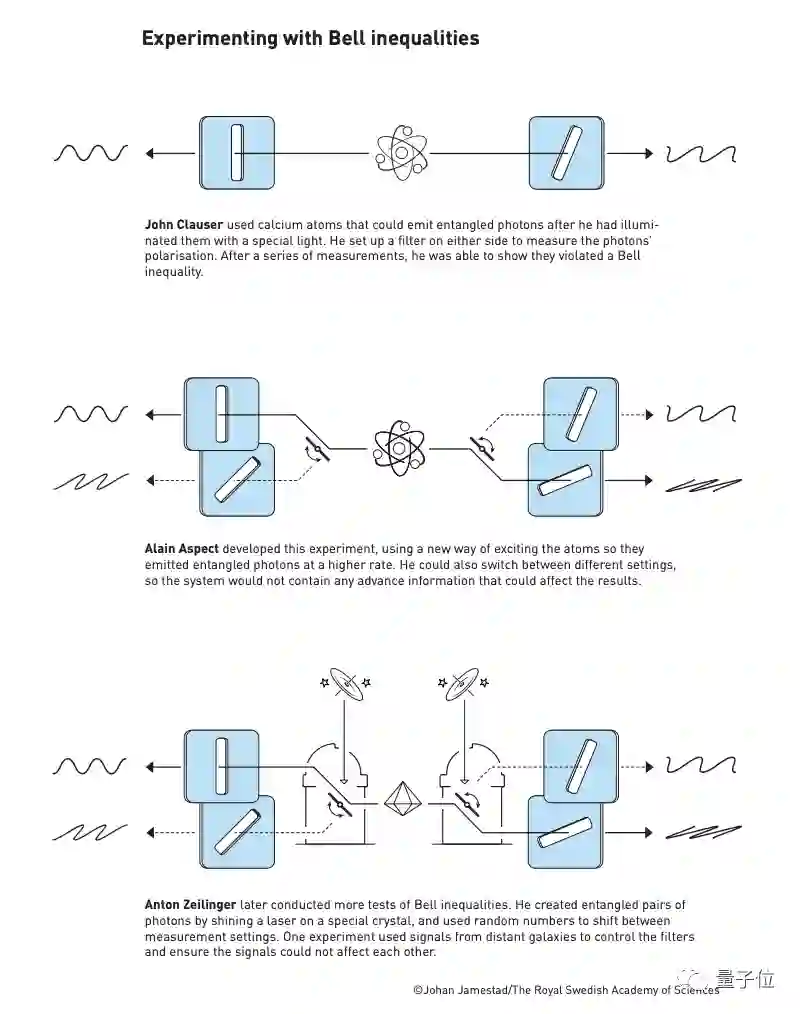
从那之后，物理学家们做了很多检试贝尔不等式的实验。这其中，约翰克劳泽与他的同事在1972年率先完成了这一实验，他通过将激光照射在特殊晶体上来创建纠缠的光子对，并使用随机数在测量设置之间切换。

图源：© Johan Jarnestad/瑞典皇家科学院

不过这个实验仍存在一定的局限性，比如在产生和捕获粒子方面效率低下，测量也是预设的。其他研究者也质疑实验结果是否存在一定的漏洞。

但十年之后，也就是1982年，当时在读博士的阿兰阿斯佩成功弥补了这一局限性，博士论文就是以这一实验为题目，他检测到了更多的光子以及测量结果也很好，最终得到的实验结果符合量子力学的预测。

换言之明确证明，量子力学是正确的，并没有像爱因斯坦所说有隐藏的变量。

如果说，前两位科学家是证明了量子力学的理论性，那么安东·塞林格则是真正将量子力学从理论推向应用，发现纠缠的量子态具有存储、传输和处理信息的潜力。

1997年塞林格及其同事首次发现，如果纠缠对中的粒子以相反的方向行进并且其中一个粒子以这样的方式遇到第三个粒子，它们就会发生纠缠，就会发生有趣的事情，即进入到一个新的共享状态，第三个粒子会失去它的身份。

这种将未知量子态从一个粒子转移到另一个粒子的方式称为量子隐形传态。

还有一位是潘建伟院士导师

其实这三位大佬在获得诺贝尔物理学奖之前，就曾一起获得过沃尔夫物理学奖（2010年）——被认为是诺贝尔物理学奖之外，物理学界最重要的奖项之一。

还是按照惯例，盘点一下这三位大佬的过往成绩。

阿兰·阿斯佩是法国物理学家，因研究“量子纠缠”而闻名。

除了研究贝尔不等式之外，Aspect还研究中性原子的激光冷却，主要参与玻色-爱因斯坦凝聚相关实验。

目前Aspect是法国科学院和技术学院的成员，也是巴黎综合理工学院的教授。

继2010年获得沃尔夫物理学奖之后，2013年获得尼尔斯·玻尔国际金奖和联合国教科文组织尼尔·玻尔奖，同年还被还被授予量子信息处理和通信的巴尔赞奖。

值得一提的是，在Aspect的过往研究履历中，有着诸多的第一：

第一个在实验证明中排除测量站之间的亚光速通信，证明量子力学使可分离隐变量理论无效；
第一个通过实验证明单光子的波粒二象性；
第一个比较了相同条件下费米子和玻色子的汉伯里布朗-特维斯相关性；
第一个证明了超冷原子系统中的安德森局域化。

约翰·克劳瑟 （John Clauser）是美国理论和实验物理学家，1964年，他获得了加州理工学院的物理学学士学位，1969年获得哥伦比亚大学物理学博士学位。

1969年至1996年，他主要在劳伦斯伯克利国家实验室、劳伦斯利福摩尔国家实验室和加州大学伯克利分校工作。

克劳瑟最广为人知的事项就是对量子力学基础的贡献，他的CHSH预测和弗里德曼-克劳泽实验被认为量子力学中非常重要的部分，目前已经成为标准物理课程（本科）的一部分。

在外界看来，他的理论之于量子力学，就相当于迈克尔逊-莫雷实验之于狭义相对论。

安东·塞林格 （Anton Zeilinger）是奥地利量子论物理学家。目前是维也纳大学物理学教授，曾任教于因斯布鲁克大学，此外，他还是奥地利科学院量子光学与量子信息研究所维也纳分所主席。

值得一提的是，塞林格还是中国科学院外籍院士，同时也是潘建伟院士的博士导师。

塞林格教授积极推动中奥国际学术交流与合作。自1983年起，他与中国科学院以及中国工程院等机构长期保持着沟通和交流，并与多家单位建立密切合作关系。

其中，利用“墨子号”量子科学实验卫星，他的团队合作参与了中科院主导的洲际量子通信实验，成果入选美国物理学会评选的2018年度国际物理学十大进展。

此外，塞林格对人才教育上还颇有兴趣。在2009年，他创立了国际学院 Traunkirchen，致力于支持科学和技术方面的天才学生。

（插句题外话）塞林格还是道格拉斯·亚当斯（Douglas Adams）的《银河系漫游指南》的粉丝，他甚至把自己的帆船命名为42号。

参考链接：
https://www.nobelprize.org/prizes/physics/

——END——