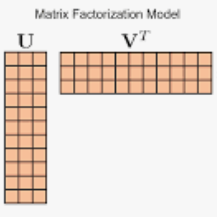
矩阵压缩算子

文 / Rina Panigrahy

矩阵压缩

张量和矩阵是机器学习模型的基本模块，尤其是在深度网络中。为了将机器学习应用于手机、智能家居助手、汽车、恒温器等设备，需要将模型压缩。这不仅有助于提升网络可用性、降低延迟 和能耗问题，同时也满足最终用户的期望：模型在设备上推理，用户数据无需离开本地，从而进一步保护用户隐私。

• 隐私
  https://venturebeat.com/2019/06/03/how-federated-learning-could-shape-the-future-of-ai-in-a-privacy-obsessed-world/

由于这类设备的存储空间、算力和电池容量都较低，所以要将模型应用其中就往往需要“偷工减料”，如限制词汇量或牺牲模型质量。因此，压缩模型的不同层中的矩阵将十分有用。主流的矩阵压缩技术包括 剪枝、低秩逼近、量化 和 随机投影。我们认为，大多数这类方法都可看作是通过某种类型的因子分解算法将矩阵分解为两个因子。

压缩方法

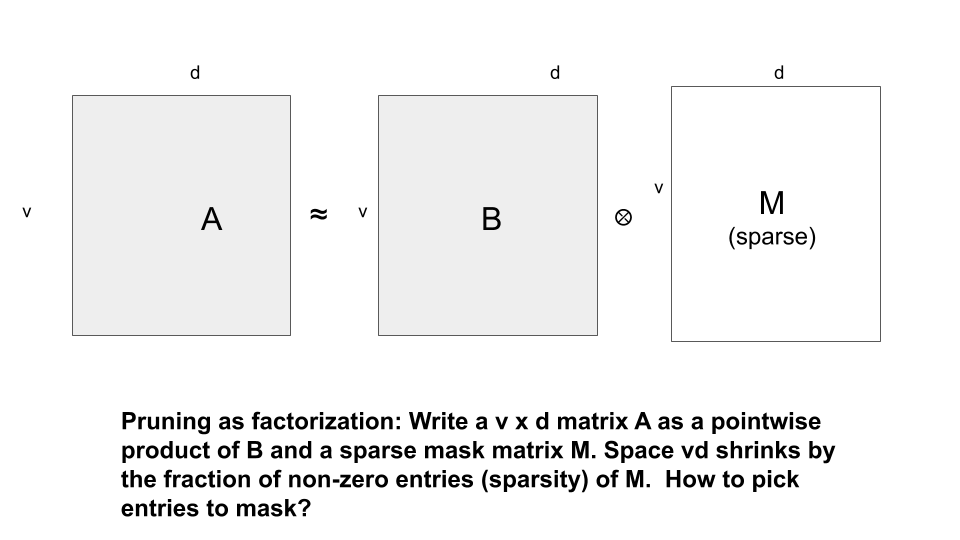
剪枝：剪枝是一种主流方法，通过减少神经网络中的参数量让矩阵稀疏化，很多时候，此方法可在不影响性能的情况下剪掉矩阵的很大一部分数据。

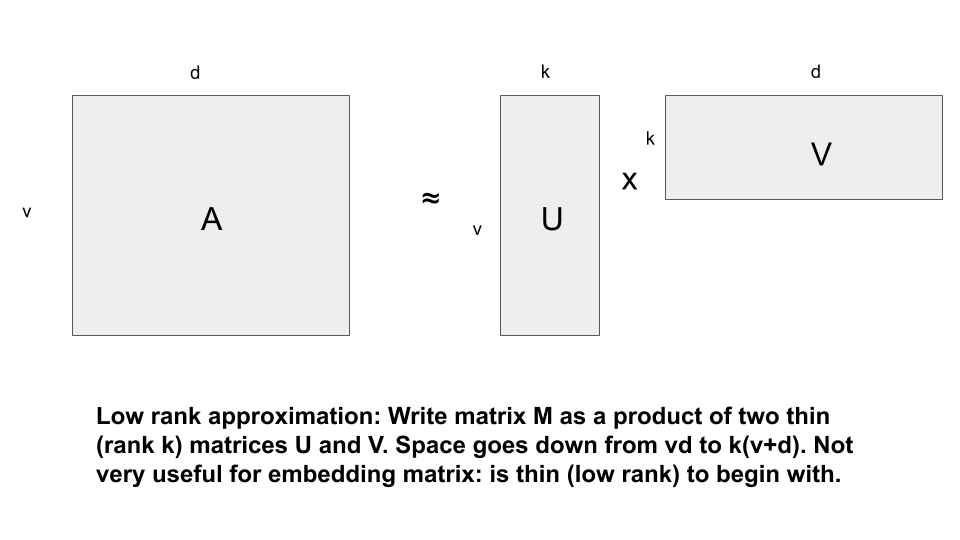
低秩逼近：另一种常见方法是低秩逼近，该方法通过最小化 Frobenius 误差 |A-UVT|F ，将原始矩阵 A 分解为两个小型矩阵，其中 U 和 V 是低秩（比如秩 k）矩阵。这一最小化可通过利用 SVD（奇异值分解）完美实现。

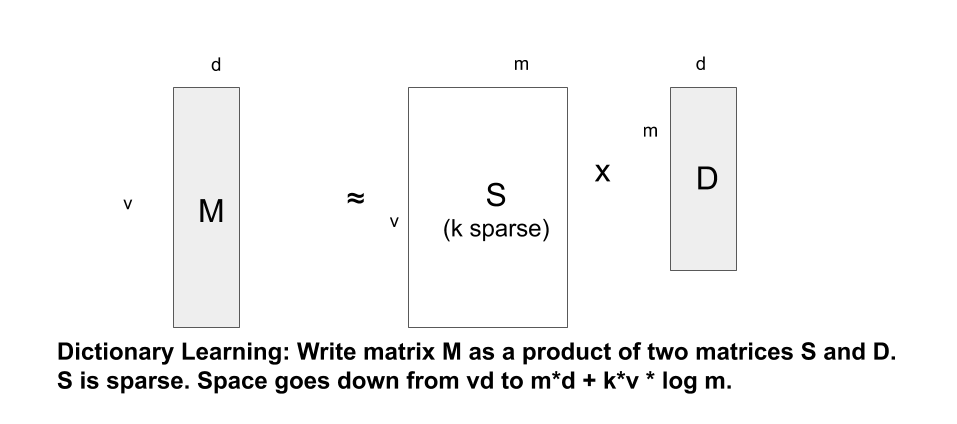
字典学习：低秩逼近的一个变体是稀疏分解，不是精简因子，而是将其稀疏化（注意，精简矩阵可视为一种特殊的稀疏，因为精简矩阵就像一个较大矩阵，只是缺少的列都为零）。稀疏分解的一种主流形式是字典学习，对于高瘦的嵌入向量表格时十分有用，这样从一开始就已经是低秩矩阵了；字典学习利用了以下可能情况：即使嵌入的值数量很大，也可能存在一个较小的基本向量字典，从而让每个嵌入向量都成为其中一些字典向量的某种稀疏组合，这样就把嵌入的矩阵分解成较小的字典表和一个稀疏矩阵的乘积，而稀疏矩阵指定为每个嵌入项组合哪些字典项。

常用的随机投影只是矩阵分解的一种特殊情况，其中一个因子是随机因子，该方法使用一个随机投影矩阵将输入投影为一个维度较小的向量，然后训练精简后的矩阵。

量化：另一种主流方法是量化，该方法通过将值四舍五入成较小的位数来量化每个值或值块，由此就能将每个值（或值块）都替换为量化代码。这样原始矩阵就分解为一个码本和一个编码表示，原始矩阵中的每个值均通过查找码本编码矩阵中的代码来获取。因此，此方法也可以视为是码本和编码矩阵的特殊积。码本可通过某种集群算法（如 k 平均法）由矩阵的值或值块计算得出。这实际上是一种特殊的字典学习，其稀疏性为 1，因为每个块都表示为代码本中的一个向量（可视为字典），而非稀疏组合。剪枝也可以视为是一种特殊的量化，其中每个值或块均指向一个代码本值，且该值为零或其自身。

因此，从剪枝到量化再到字典学习是一个连续过程，此过程与低秩逼近一样，都是矩阵分解的一种形式。

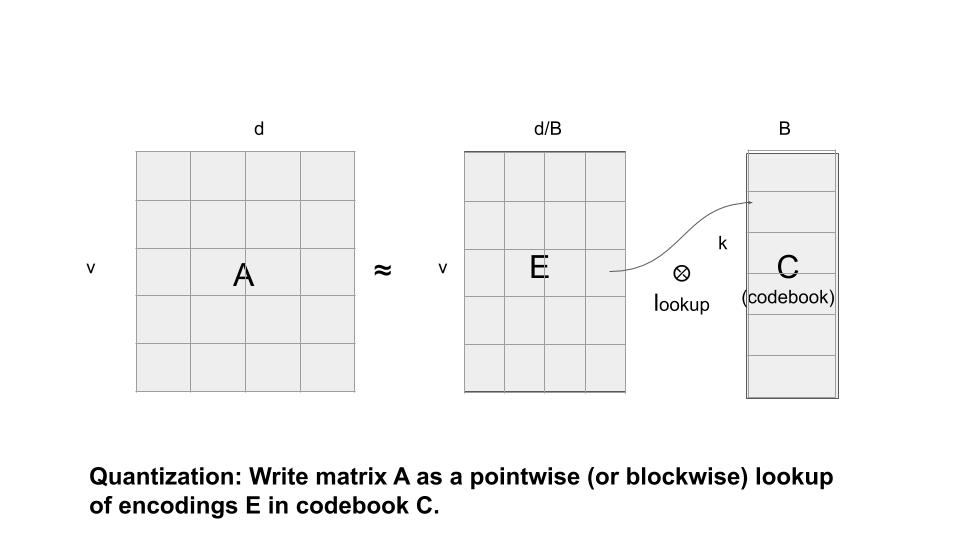
将因子分解视为变异

应用这些不同类型的矩阵分解可看作是通过将一层拼接成两层的乘积来实现网络架构变异。

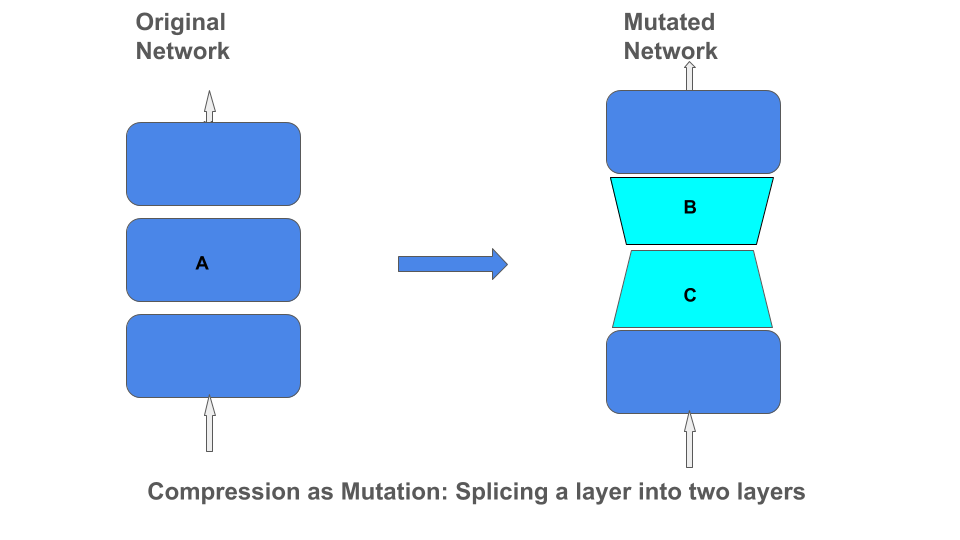
TensorFlow 矩阵压缩算子

面对大量的矩阵压缩算法，如果可以对 TensorFlow 矩阵应用一个简单算子，在训练期间利用任何这些算法来压缩矩阵，那么将十分方便。这样就不必先训练完整矩阵，应用分解算法来创建因子，再创建另一模型，可能还要重复训练其中某个因子，从而节省开销。例如，对于剪枝算法，识别出掩膜矩阵 M 后，可能还希望继续训练非掩模值。类似地，在字典学习方法中，可能会继续训练字典矩阵。

我们已经开源一个此类压缩算子，其可采用某个 MatrixCompressor 类中指定的任何定制矩阵分解方法。然后，要应用某个压缩方法，只需调用 apply_compression(M, compressor = myCustomFactorization)。此算子会自动将单个矩阵 A 替换为两个矩阵的乘积 B*C，而这两个矩阵是通过采用指定的定制分解算法分解 A 得到。实际操作中，此算子会让矩阵 A 训练一段时间，并在某个训练快照上应用分解算法，将 A 替换为因子 B*C，然后继续训练因子（乘法“*”并不一定是标准矩阵乘法，可以是压缩类中指定的任何自定义方法）。压缩算子可以采用之前提到的任何一种分解算法。

• 开源一个此类压缩算子
  https://github.com/google-research/google-research/tree/master/graph_compression

对于字典学习方法，我们甚至有一种 基于 OMP 的字典学习实现方法，该方法比 scikit 实现速度更快。另外我们还有一种改进的基于梯度的剪枝方法，该方法不仅考虑值的量级以决定被剪对象，还通过度量与值有关的损失梯度估计对最终损失的影响。

• 基于 OMP 的字典学习实现
  https://github.com/google-research/google-research/tree/master/dictionary_learning

• scikit 实现
  https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.DictionaryLearning.html

• 基于梯度的剪枝
  https://drive.google.com/file/d/1TeuWJ-clTa30andouyYNYn4Vh1bHMC2J/view?usp=sharing

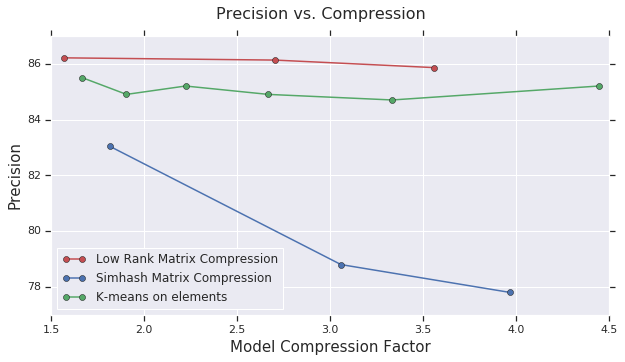
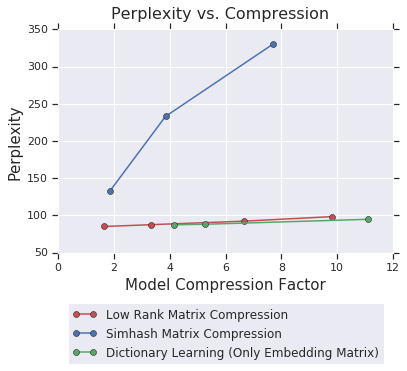
因此，我们正在执行的是实时网络变异，开始只有一个矩阵，最后层中产生了两个矩阵。我们的分解算法甚至不一定需要基于梯度，而是可以涉及更多离散形式的算法，如哈希、用于字典学习的 OMP 或者 k 均值聚类。由此，我们的算子表明，可以将基于梯度的连续方法与更多传统的离散算法组合使用。本试验还包含一种基于随机投影的名为 simhash 的方法，其中要压缩的矩阵乘以一个随机投影矩阵，并将值四舍五入为二进制值，这样就分解为一个随机投影矩阵和一个二进制矩阵。下图显示如何对 CIFAR10 和 PTB 的压缩模型执行这些算法。结果表明，对于 CIFAR10，低秩逼近比 simhash 和 k 均值法效果要好，而对于 PTB，字典学习则比低秩逼近方法略胜一筹。

• simhash
  https://drive.google.com/file/d/1tUJXs8bFVsp5A3Ay2CiiB0R6Eq2mqicc/view?usp=sharing

• CIFAR10
  https://www.cs.toronto.edu/~kriz/cifar.html

• PTB
  https://catalog.ldc.upenn.edu/LDC99T42

CIFAR10

PTB

结论

我们开发出一个算子，该算子可采用充当因子分解方法的任何矩阵压缩函数，并创建一个 TensorFlow API，以便在训练过程中对任何 TensorFlow 变量动态地应用此类压缩。我们通过几种不同的因子分解算法（包括字典学习）演示了其用法，并展示了对于 CIFAR10 和 PTB 模型的试验结果。同时还阐述了如何实现离散过程（如稀疏矩阵分解和 k 平均聚类）与连续过程（如梯度下降）的动态组合。

致谢

此项研究的成功离不开 Xin Wang、Badih Ghazi、Khoa Trinh、Yang Yang、Sudeshna Roy 和 Lucine Oganesian 的付出。同时也要感谢 Zoya Svitkina 和 Suyog Gupta 的帮助。

了解更多请点击 “ 阅读原文 ” 访问 Github。