OpenAI 推出数学推理证明模型，推理结果首次被数学家接受

今年 6 月，OpenAI 发布一款强大的文本生成模型 GPT-3，不少网友迅速上手用了起来，有人用它写食谱、写歌词，甚至有人用它写博客，愣是以假乱真登上了新闻平台技术板块热榜第一。

 

前不久，OpenAI 再次放出大招。这次，研究人员发布了一篇论文《Generative Language Modeling for Automated Theorem Proving》，推出了一款用于自动定理证明 (ATP) 的 GPT-f 模型。GPT-f 基于 Transformer 语言模型，可以为 Metamath 形式化语言提供自动证明器和证明助手。

论文地址：

https://arxiv.org/pdf/2009.03393.pdf

GPT-f 有什么特别之处？

 

论文一作 Stanislas Polu 在推特上进行了介绍，他们在实验中发现，GPT-f 比现有自动定理证明器还要优秀，可完成测试集中 56.22% 的证明，而现有的 SOTA 模型 MetaGen-IL 也只能证明 21.16% 的定理。

 

此外，GPT-f 还发现了新的简短证明，已有 23 个简短证明被收入 Metamath 函式库中。这是深度学习模型的定理生成证明首次被数学家接受。

 

那么大家对于 GPT-f 是怎么看的呢？

网友普遍保持中立，大佬认为没有特别之处

 

文摘菌想在推特上看看网友们的讨论，没想到 AI 界的一些大佬也发表了自己的看法。

 

Robust.AI、Geometric Intelligence 两家 AI 公司的创始人，研究人工智能领域多年的科学家 Gary Marcus 认为，“就像 GPT-3 不是研究真正人类语言的正确方向一样……， GPT-f 并不是达到真正人类水平 (更不用说超越人了) 的数学定理证明的正确研究方向。”

 

他还称，人们一直在误用 GPT 来解决它不适合解决的问题，同样的问题也不断出现。

 

 

美国通用人工智能会议主席、奇点大学顾问、人工智能软件公司 Novamente LLC 公司董事长   Ben Goertzel 也在推特发表了自己的看法，他认为，GPT-f 又是一个在不理解的情况下指导定理证明的古怪实验……

 

 

他还专门写了一篇文章来谈论对于 GPT-f 的看法，发表在了自己的博客上。

 

博客地址：

http://multiverseaccordingtoben.blogspot.com/2020/09/gpt-f-one-more-funky-experiment-in.html

 

Ben 还在博客中写道，“从 ATP 领域正在进行的工作的总体背景来看，在我看来，GPT-f 不像 GPT-2 或 GPT-3 那样迈出了一大步——但可以肯定的是，它在 ATP 方面是有意义的进展，与这一领域其他专家正在进行的大量研究进展相符（然而，这些专家因为没有像 OpenAI 那样的公关预算而不被媒体报道）。GPT-f 还有一个与其他 GPT 类似的核心缺点——它在理解数学这方面并不比 GPT-2 或 GPT-3 理解语言的能力更强。”

 

那网友们怎么看呢？

 

现阶段网友们普遍是一种吃瓜的态度，并没有对 GPT-f 大肆夸耀。大部分只是转发了相关推文并陈述了论文中 GPT-f 实验的成果。

 

也有一部分网友在论坛中发表了自己的疑问。

 

比如网友@Jason Rute 就问到：什么才是有效的证明步骤？Jason Rute 曾经是一名数学家，后来成为了数据科学家，他对深度学习很感兴趣。

 

GPT-f 将同时返回一个定理和替换，然后它们必须与目标统一。如果替换不统一，那么我确定它被标记为无效。然而，如果这个定理不在先前证明的定理列表中呢？GPT-f 是做什么的？

1）试着证明这个定理；

2）认为这是一个无效的证明步骤，还是将输出限制在已知的定理上？

（我想会是第一条，但我还是想验证一下。）

 

论文一作 Stanislas Polu 也在论坛对此进行了回复，并表示这是个好问题。

 

• 如果统一失败，内核会拒绝验证步骤，甚至在验证树搜索中也不会考虑它（不会添加到树或队列中，也不会由值函数赋值）。

• 如果该定理在数据库中没有被报告，那么该定理也将被拒绝。这就是说，我们正在试验让模型证明这些猜想，如果它们被价值函数认为有趣的话。在这种情况下，我们只需将定理本身添加为子目标（带有一个特殊的标记，以确保一旦找到证据，我们就重新检查不同的变量（DVs 是一种元数学技术，可以在您的思维中抽象出来，如果您不知道它们是如何工作的，可以稍后再访问）），然后子目标会相应地被赋值并添加到队列中。

针对这个问题，Jason Rute 在论文作者回复后还追加了提问，详细讨论可以看这里：

https://leanprover-community.github.io/archive/stream/219941-Machine-Learning-for-Theorem-Proving/topic/GPT-f.20paper.html#210087032

 

Jason Rute 还说，“在许多方面 GPT-f 类似于之前出现的其他定理证明，HOList/DeepMath, CoqGym/ASTTactic, TacticToe 等等。所有这些的共同之处在于它们把定理证明当作树搜索。长期以来，我们所知道的是，采用智能启发式可以避免树(和图)搜索中的组合爆炸。AlphaGo 及其后继者告诉我们的是，这些启发式完全可以从例子中学习，也可以从引导和强化学习中学习。GPT-f 在这方面没有什么不同。(关于 GPT-f 使用的特定树搜索算法，我不打算说得太多，因为我不认为他们的方法比其他类似的论文优化很多。)”

 

此外，文摘菌也翻了一下知乎，只有一个相关问题，而且该问题下只有一个回答。由此可见，国内网友可能还不太知道 GPT-f，也可能由于发布时间并不长，大家对于GPT-f 还处在比较懵的状态。

 

 

如果你对 GPT-f 有更好的了解或看法，欢迎在评论区分享~

 

GPT-f 由自动证明器和证明助手组成

GPT-f 是由两部分组成的，分别是自动证明器和证明助手。

 

自动证明器是为了寻求更简短的证明，研究人员从 Metamath 的 set.mm 库中采样命题证明，并对比 GPT-f 模型找到的解与真值的长度，同时还验证了简短证明不依赖于额外的公理。

 

     

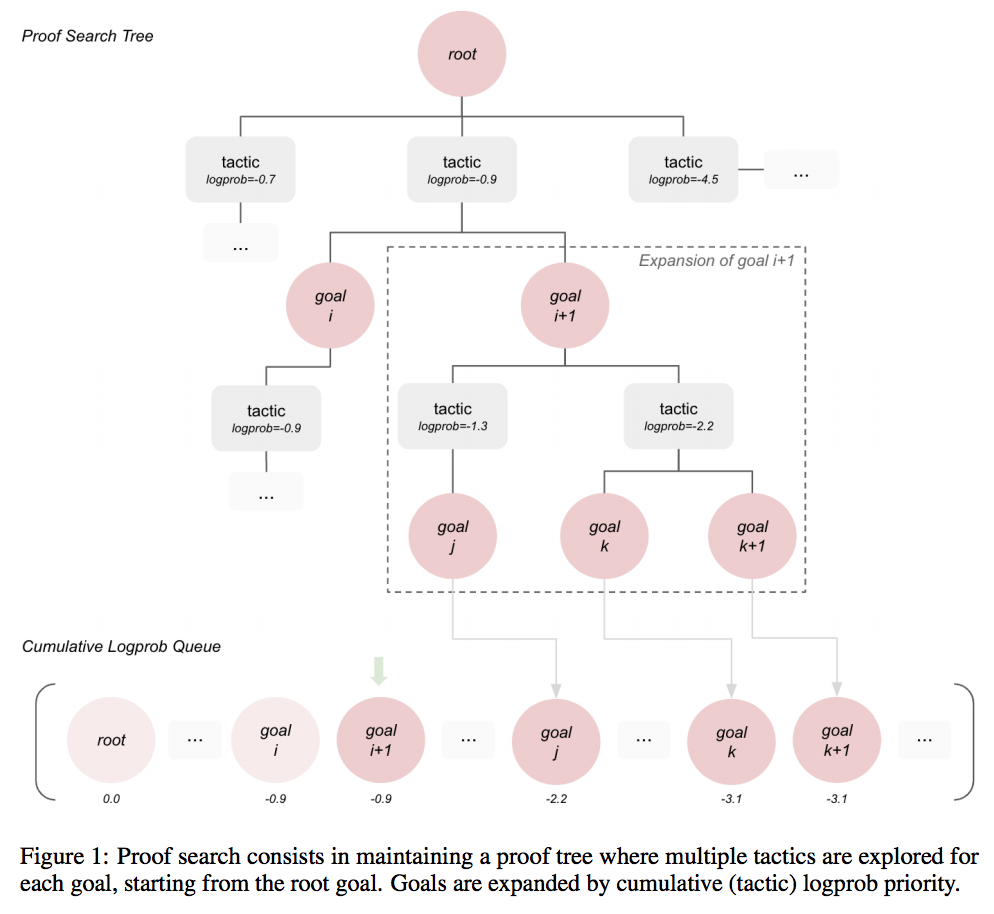
证明搜索包括维护一个证明树，其中从根目标开始探索每个目标的多种策略。

 

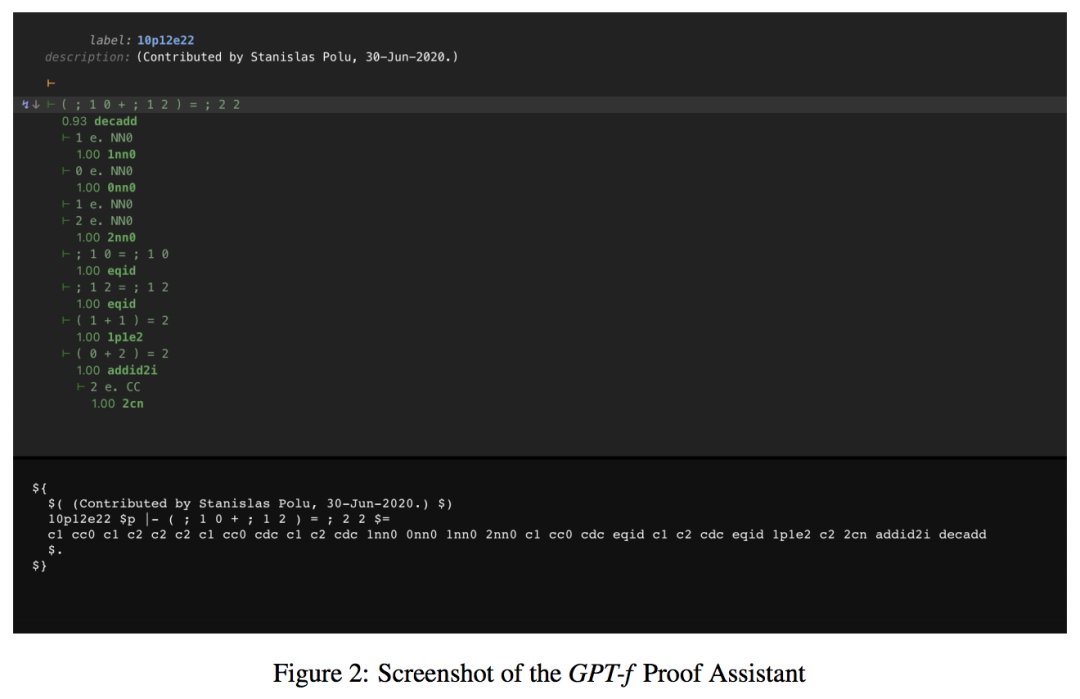
OpenAI 利用在线证明助手，来帮助模型产生交互式的证明架构。下图展示了 GPT-f  证明助理的界面：

 

 

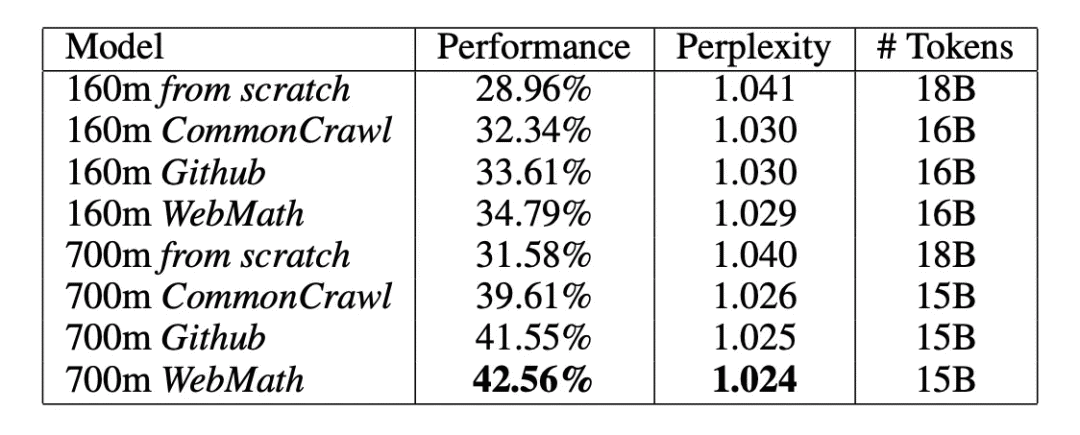
Metamath 是一种用于存档，验证和研究数学证明的语言和计算机程序。研究人员使用 Metamath 作为正式环境，使用类似于 GPT-2 和 GPT-3 的仅解码器的转换器来创建具有各种预训练数据集和不同大小的模型。他们最大的模型具有 36 层和 774m 可训练参数。

 

各种模型大小和预训练数据集的性能

 

说了这么多，那什么是自动定理证明呢。

 

百度百科中是这样描述的：自动定理证明是人工智能研究领域中的一个非常重要的课题，其任务是对数学中提出的定理或猜想寻找一种证明或反证的方法。因此，智能系统不仅需要具有根据假设进行演绎的能力，而且也需要一定的判定技巧。

 

研究人员发现，学习证明定理与学习玩棋盘游戏之间有相似之处，因为它们都提供了自动确定成功的方法，并生成新的数据。因此，AlphaZero 在围棋领域的成功表明，自动定理证明可能是神经网络推理研究的一个富有成效的领域。

 

相关讨论及参考：

https://www.reddit.com/r/MachineLearning/comments/ipdu7m/r_gptf_a_new_sota_for_automated_mathematical/

https://medium.com/@raevskymichail/gpt-f-neural-network-theorem-proofs-28caacba5468

http://ai.chinabyte.com/239/714875739.shtml

https://syncedreview.com/2020/09/10/openai-gpt-f-delivers-sota-performance-in-automated-mathematical-theorem-proving/

来源：大数据文摘

点击 阅读原文 ，查看更多精彩！

喜欢本篇内容，请 分享、点赞、在看