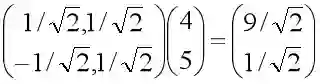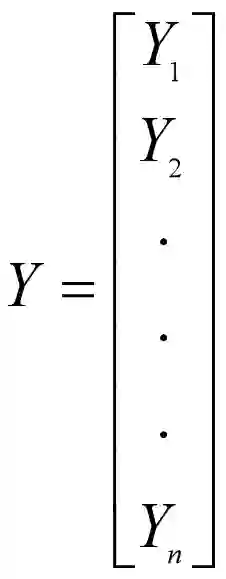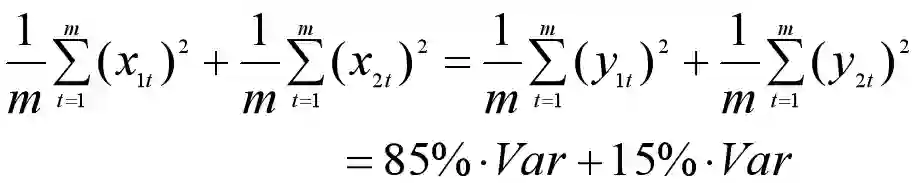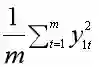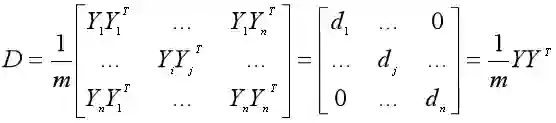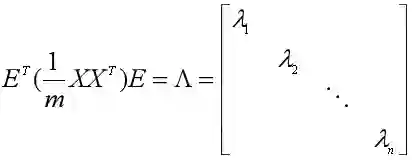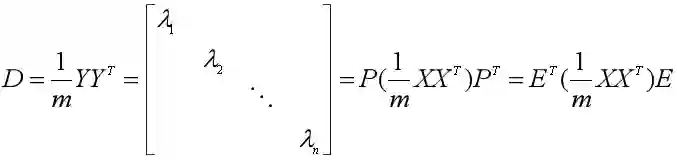主成分分析法：NLPer的断舍离（上篇）

一：今日感慨

P大的事情，让人唏嘘不已。

下面的歌词，仿佛就是悲剧的注脚：

怪我对你太执迷，让我变得不像自己。

我想要你的绽放，就把我埋葬。

你的爱带着控制，幽默也带着讽刺。

像木偶忘了认知，我怕事，你放肆。

人生需要PCA，需要断舍离。

二：内容预告

NLP还没学明白，又得开始学推荐算法。

头秃指日可待。

矩阵分解是推荐算法的一个重要分支，把用户-商品大矩阵，分解为用户偏好和商品属性两个小矩阵，其实也就是一种断舍离。

为了顺滑过渡，先来复习一下断舍离的方法：

• 主成分分析法（Principal Component Analysis，PCA）

• 奇异值分解（Singular Value Decomposition，SVD）

本篇文章复习主成分分析法，主要关注以下内容：

• 主成分分析法的思想

• 主成分的选择

• 主成分矩阵的求解

• 主成分的方差贡献率

• 基于投影方差最大化的数学推导

理解得可能不是很准确，如有错误，请发自拍。

三：主成分分析法的思想

我们在研究某些问题时，往往需要处理多变量数据，比如研究房价的影响因素，需要考虑的变量有物价水平、土地价格、利率、就业率、城市化率等。

多变量可以提供更丰富的信息，但也容易带来噪音和冗余，因为各变量之间存在一定的相关性。

那么我们可以从存在强相关性的多个变量中选择一个，或者将几个变量综合为一个变量，作为几个变量的代表。

以少数变量代表所有的变量，来解释所要研究的问题，就能化繁为简，这也就是降维的思想。

主成分分析法，就是一种运用线性代数来进行降维的方法，它将多个变量转换为少数几个不相关的综合变量，来比较全面地反映整个数据集的信息。

主成分分析法，用较少的变量来综合原始变量的信息，我们称这些综合变量为主成分，各主成分之间彼此不相关，即所反映的信息不重叠。

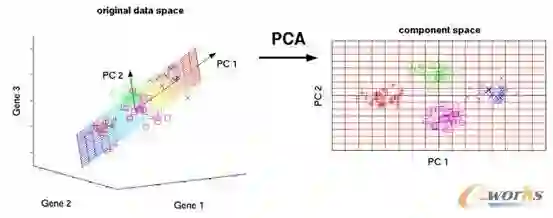
那么主成分分析法是如何降维的呢？

我们可以从坐标变换的角度来获得一个感性的认识。

我们先从最简单的情形开始：假定数据集中的原始变量只有两个，即数据是二维的，每个观测点都可以用标准的X-Y坐标轴来表示。

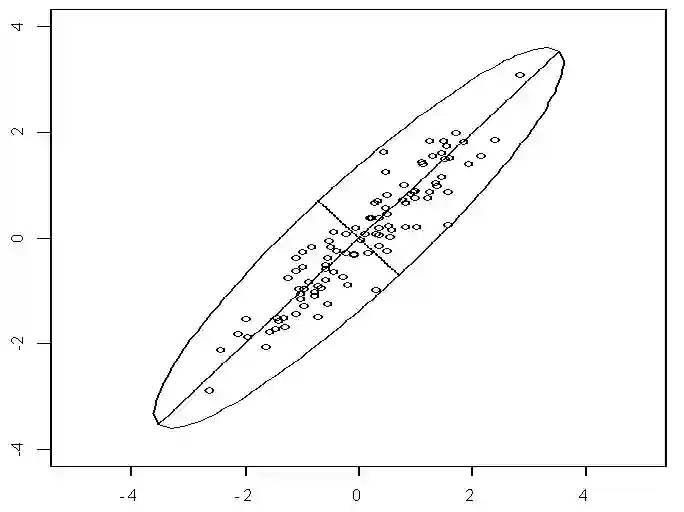
如果每一个维度都服从正态分布（这比较常见），那么这些数据会形成椭圆形状的点阵。

如下图所示，椭圆有一个长轴和一个短轴，二者是相互垂直的。

在短轴上，观测点数据的变化比较小，如果把这些点垂直地投影到短轴上，那么有很多点的投影会重合，这相当于很多数据点的信息都没有被充分利用到。

而在长轴上，观测点的数据变化比较大。

因此，如果让坐标轴和椭圆的长短轴平行或重合，那么长轴代表的变量，描述了数据的主要变化，而代表短轴的变量，描述的是数据的次要变化。

在极端情况下，短轴退化成一个点，那么就只能用长轴代表的变量来解释数据点的所有变化，也就是把二维数据降至一维。

但是，坐标轴通常并不和椭圆的长短轴平行，就像上图所展示的那样。

因此，需要构建新坐标系，使得新坐标系的坐标轴与椭圆的长短轴重合或平行。

这需要用到坐标变换，把观测点在原坐标轴的坐标转换到新坐标系下，同时把原始变量转换为长轴的变量和短轴的变量。

这种转换是通过对原始变量进行线性组合而完成的。

比如一个观测点在原X-Y坐标系中的坐标为(4,5)，坐标基为（1,0）和（0,1），如果长轴为斜率是1的线，短轴为斜率是-1的线，新坐标系以长轴和短轴作为坐标轴，那么新坐标基可以取为（1/√2, 1/√2）和（-1/√2, 1/√2）。

我们把两个坐标基按行放置，作为变换矩阵，乘以原坐标，也就是对原坐标进行线性组合，可以得到该点在新坐标系下的坐标。

可以看到，坐标变换后，长轴变量的值远大于短轴变量的值。

如果长轴变量解释了数据集的大部分变化，那么就可以用长轴变量来代表原来的两个变量，从而把二维数据降至一维。

椭圆的长轴和短轴的长度相差越大，这种做法的效果也就越好。

接着我们把二维变量推广到多维变量。

具有多维变量的数据集，其观测点的形状类似于一个高维椭球。

同样，把高维椭球的轴都找出来，再把代表数据大部分信息的k个最长的轴作为新变量（相互垂直），也就是k个主成分，那么主成分分析就完成了。

选择的主成分越少，越能体现降维二字的内涵，但不可避免会舍弃越多的信息。

四：主成分的选择

到这里，我们应该有三个问题需要思考：

• 一是怎么得到坐标变换的矩阵呢？
• 二是怎么衡量一个主成分所能解释的数据变化的大小呢？
• 三是按什么标准来决定选多少个主成分呢？

首先来解决第二和第三个问题。

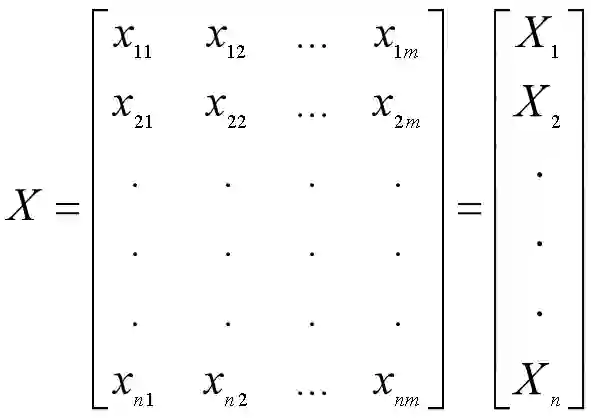
假定我们有m个观测值，每个观测值有n个特征（变量），那么将其排成n行m列的矩阵，并且每一行都减去该行的均值，得到矩阵X（减去均值是为了下面方便求方差和协方差）。

再按行把X整理成n个行向量的形式，即用X₁, X₂, ..., X_n来表示n个原始变量。

上面的例子说明了，通过一个n×n的转换矩阵对数据集中的原始变量进行线性组合，就可以得到n个新的变量。

转换矩阵可以有很多个，也就是用于变换的坐标系有很多个，但是只有一个可以将原始变量转换而得到主成分。

我们先不管这个矩阵是怎么得到的，假定我们已经得到了这个转换矩阵P，把转换后的n个主成分记为Y ₁ , Y ₂ , ..., Y _n ，那么由Y=PX，就可以得到主成分矩阵：

这n个行向量都是主成分，彼此之间是线性无关的，按照对数据变化解释力的强度降序排列（并非被挑出来的前k个行向量才叫做主成分）。

那么如何衡量每一个主成分所能解释的数据变化的大小呢？

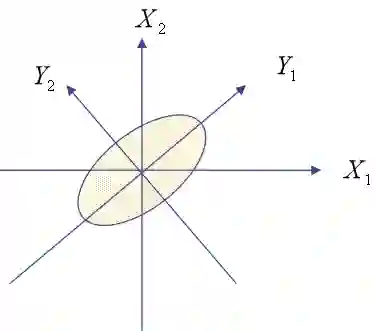
我们先看n=2时，主成分为Y₁和Y₂，原变量为X₁和X₂。

从下图可见Y₁为长轴变量，数据沿着这条轴的分布比较分散，数据的变化比较大，因此可以用Y₁作为第一主成分来替代X₁和X₂。

那用什么指标来量化数据的变化和分散程度呢？

用方差！

我们把向量X₁和X₂的元素记为x_1t、x_2t（t=1,2,...,m），把主成分Y₁和Y₂的元素记为y_1t、y_2t（t=1,2,...,m），那么整个数据集上的方差可以表示如下（数据早已经减去均值，所以行向量的均值为0）。

第一主成分Y₁所能解释的数据的变化，可以用主成分的方差来衡量，也就是：

也可以用主成分的方差占总体方差的比重来衡量，这里假设为85%，这个比例越大，则反映的信息越多。

我们回到有n个原始变量和n个主成分的例子，选择合适的转换矩阵P来计算得到主成分矩阵Y时，要让单个主成分在数据集上的方差尽可能大。

那么选择主成分的一般标准是：少数k个主成分（1≤k<n）的方差占数据集总体方差的比例超过85%。

于是我们初步解决了第二个问题和第三个问题，也就是如果已知转换矩阵P和主成分矩阵Y，那么就用一个主成分的方差占数据集总体方差的比例，来衡量该主成分能解释的数据集方差的大小。

然后按这个比例从大到小进行排序，并进行累加，如果到第k个主成分时，累加的比例恰好等于或者超过85%，那么就选择这k个主成分作为新变量，也就是对原始特征变量进行了降维。

接下来回到第一个问题，也就是求解第二个问题和第三个问题的前提：转换矩阵P怎么算出来？

五：转换矩阵的计算

主成分矩阵Y 有两个特点：

一是单个主成分向量Y_i的方差占总体方差的比例尽可能大，而且按照方差占比的大小，对所有的主成分进行降序排列。

二是所有主成分都是线性无关的，或者说是正交的。所有主成分中，任意两个主成分Y_i和Y_j的协方差都是0。

第一个特点涉及主成分的方差，第二个特点涉及主成分之间的协方差。

这自然而然让我们想到协方差矩阵的概念，因为主成分矩阵Y的协方差矩阵的对角元素，就是每个主成分的方差，而非对角元素就是协方差。

由于协方差为0，那么主成分矩阵的协方差矩阵为一个对角矩阵，且对角元素是降序排列的！

由于数据集已经减去了均值，那么主成分矩阵中的行向量也是0均值的，于是某两个主成分的协方差为：

进一步得到主成分矩阵Y的协方差矩阵为：

已知主成分矩阵Y的协方差矩阵是对角矩阵，对于我们求出转换矩阵P和主成分矩阵有什么用呢？

有的，我们把Y=PX这个等式代入协方差矩阵中进行变换，就把已知的数据X和需要求的P都放到了协方差矩阵中：

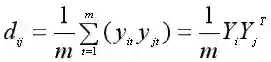
比较神奇的是，主成分矩阵Y的协方差矩阵可以由数据集X的协方差矩阵得到。

数据集X的协方差矩阵显然是一个实对称矩阵，实对称矩阵有一系列好用的性质：

• n阶实对称矩阵A必然可以对角化，而且相似对角阵的对角元素都是矩阵的特征值。
• n阶实对称矩阵A的不同特征值对应的特征向量是正交的（必然线性无关）。
• n阶实对称矩阵A的某一特征值λ_k如果是k重特征根，那么必有k个线性无关的特征向量与之对应。

因此数据集X的协方差矩阵作为n阶实对称矩阵，一定可以找到n个单位正交特征向量将其相似对角化。

设这n个单位特征向量为e₁, e₂, ..., e_n，并按列组成一个矩阵：

那么数据集X的协方差矩阵可以对角化为：

相似对角阵上的元素λ₁、λ₂、... 、λ_n是协方差矩阵的特征值（可能存在多重特征值），E中对应位置的列向量是特征值对应的单位特征向量。

接下来是高能时刻。

我们把这个对角阵Λ上的元素从大到小降序排列，相应的把单位特征向量矩阵E里的特征向量也进行排列。

我们假设上面已经是排列好之后的形式了，由于主成分矩阵的协方差矩阵也是元素从大到小降序排列的对角矩阵，那么就可以得到：

也就是取X的协方差矩阵的单位特征向量矩阵E，用它的转置E^T作为转换矩阵P，而X的协方差矩阵的特征值λ就是各主成分的方差！

有了转换矩阵P，那么由PX我们自然可以得到主成分矩阵Y。

如果我们想把数据从n维降至k维，那么从P中挑出前k个行向量，去乘以数据集X，就可以得到前k个主成分。

至此第一个问题，转换矩阵P和主成分矩阵的求解，也可以完成了。

END

推荐阅读

AINLP年度阅读收藏清单

当当的羊毛，快薅，这一次要拼手速！

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

From Word Embeddings To Document Distances 阅读笔记

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

可解释性论文阅读笔记1-Tree Regularization

征稿启示 | 稿费+GPU算力+星球嘉宾一个都不少

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。