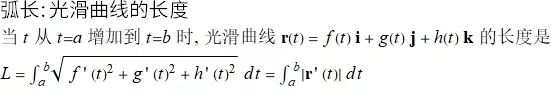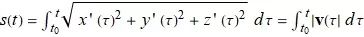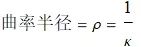10.6 弧长和单位切向量 T
现在来看下曲线形状的特征, 这些特征能描述曲线弯曲和扭曲的程度.
曲线的弧长
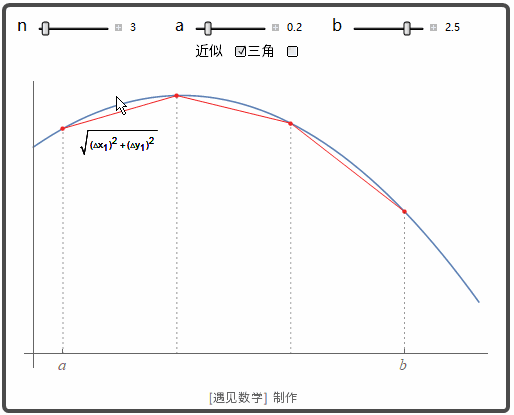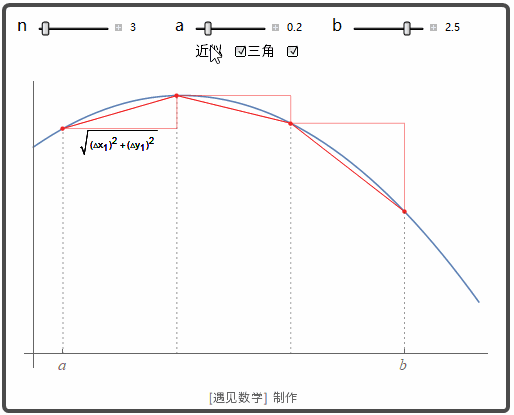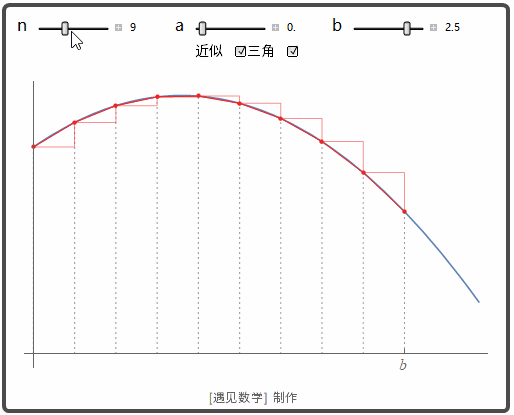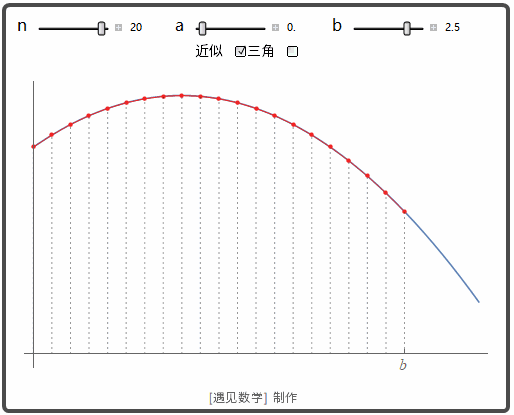
来看看怎样定义光滑曲线的距离. 其实与平面曲线一样, 观察下面动图:
![]()
![]()
弧长函数
选取以 t 为参数 曲线 C 上的点 P(t0)
P(
t
0
)
为基点, t 的每个值确定 C 上的一个点 P(t)=⟨x(t),y(t),z(t)⟩
P(t)=
⟨
x(t),y(t),z(t)
⟩
和一个沿曲线从基点测量起的距离 s(t) 函数:
![]()
s 的每个值确定 C 上的一个点, s 称为曲线的弧长参数, 对于研究空间曲线的弯曲和扭转非常有用.
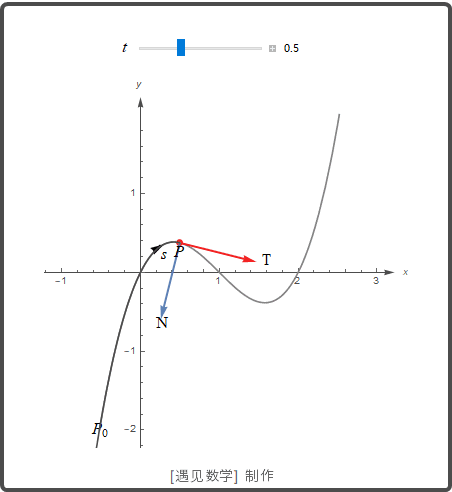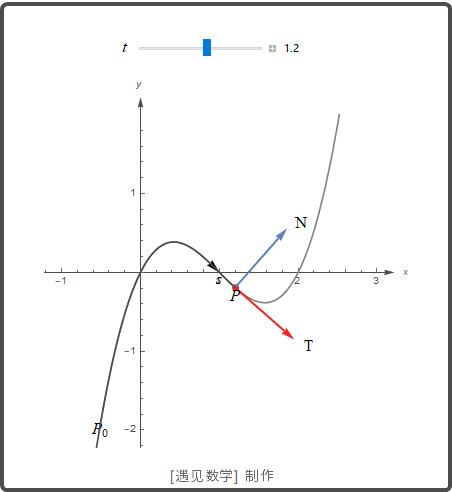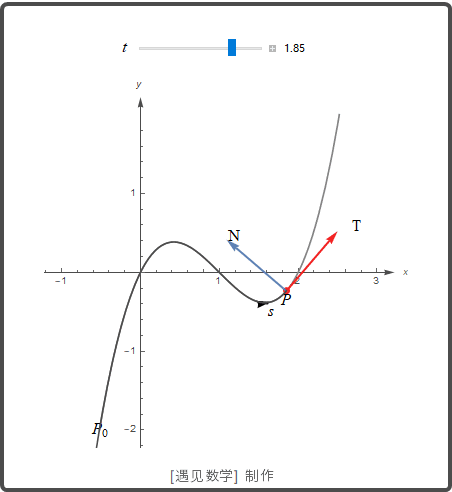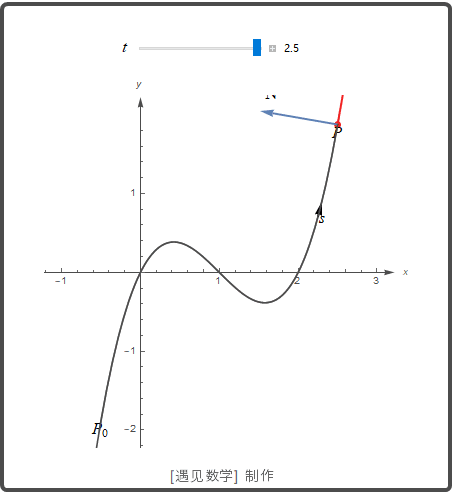
单位切向量 T
速度向量 v=dr/dt 切于曲线, 从而向量 T=v/|v| 是曲线的单位切向量, 它是描述空间物体运动标架的三个向量之一.
![]()
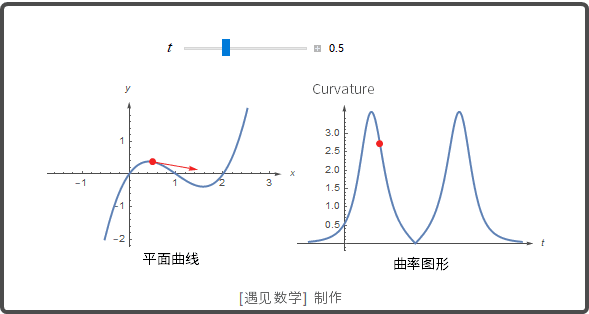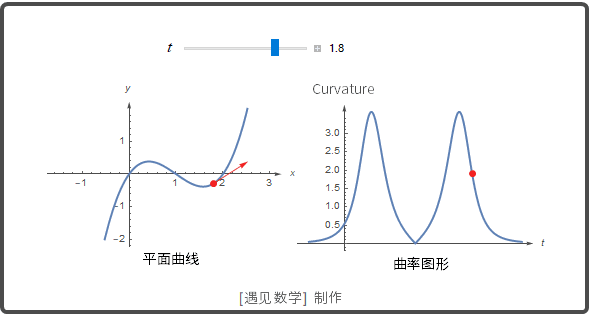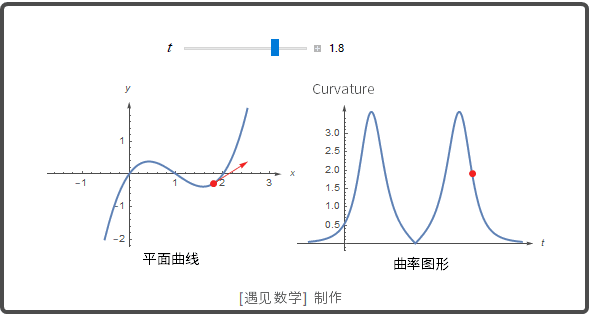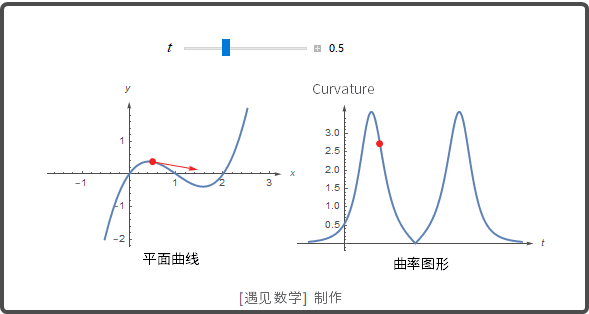
曲率和平面曲线的主单位法向量
曲线的"弯曲"和"扭曲"并不是相同. 当一个质点沿平面光滑曲线运动时, T=dr/ds 随曲线的弯曲而转动. T 是单位向量, 在质点沿曲线运动时它的长度保持常值而仅仅方向改变. 单位长度 T 的转动率为曲率, 用希腊字母 [Kappa] 记号(读 kappa).
![]()
如果\left\left| rac{T}{s}ightight|\left\left| rac{T}{s}ightight|大, T 在质点通过 P 时转动得就急剧, 在点 P 的曲率就大, 反之亦然. 可以观察下图:
![]()
当曲线弯曲时, 向量 dT/ds 指向 T 转动的方向. 也就是说, 主单位法向量指向曲线凹的一侧. 观察下面动图:
![]()
![]()
曲率圆和曲率半径
在平面曲线的 [Kappa]!=0 的点 P 的曲率圆是曲线所在平面上的圆周:
它在点 P 切于曲线(跟曲线有同样的切线)
它在点 P 跟曲线有同样的曲率
位于曲线的凹的一侧.
曲线在点 P 的曲率半径是曲率圆的半径:
![]()
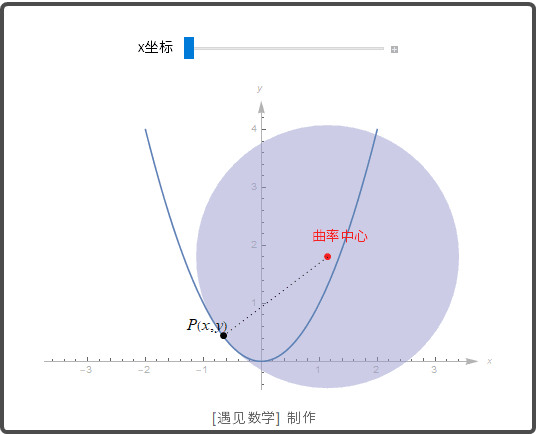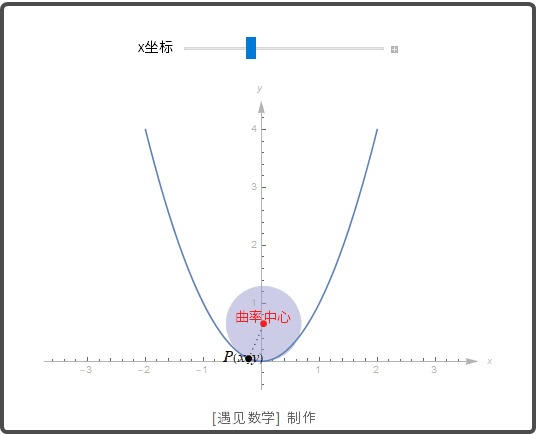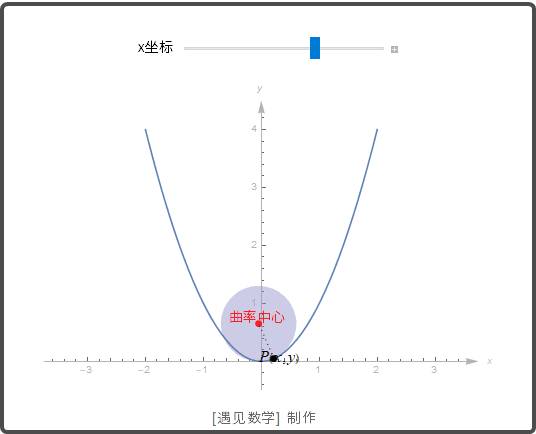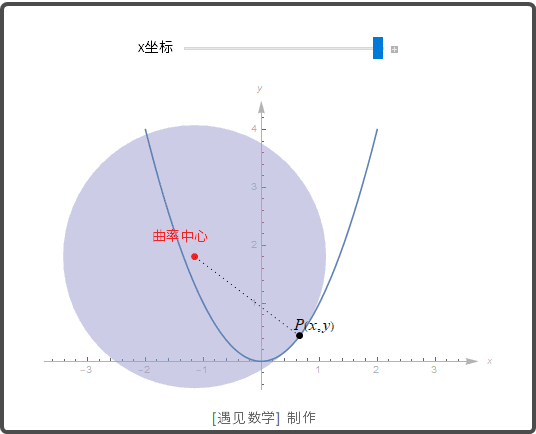
下面观察 y=x2
y=
x
2
的曲率圆动画:
![]()