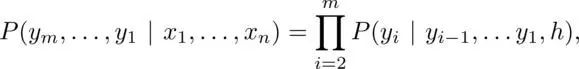扔掉代码表!用RNN“破解”摩斯电码
更多干货内容请关注微信公众号“AI 前线”,(ID:ai-front)
剧透警告:其实 Morse 电码并不需要破解。它很有用,因为可以用最少的设备来发送消息。我之所以说它不需要破解,是因为这种代码是众所周知的,点和破折号的组合并不是什么秘密。但是从理论上讲,它是一种替代密码(substitution cipher):每个字母和每个数字都是使用点和破折号来表示,如下图所示:
AI 前线:Morse 电码是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号。它发明于 1837 年。Morse 电码是一种早期的数字化通信形式,但是它不同于现代只使用零和一两种状态的二进制代码,它的代码包括五种: 点、划、点和划之间的停顿、每个词之间中等的停顿以及句子之间长的停顿。
让我们先不要怀疑,假设我们收到了 Morse 电码的消息,但我们不知道如何解读。假设我们还有一些代码示例和它们对应的单词。现在,我们可以推测它是一种替代密码,然后我们可以最终计算出每个字母的代码,从而解码消息。
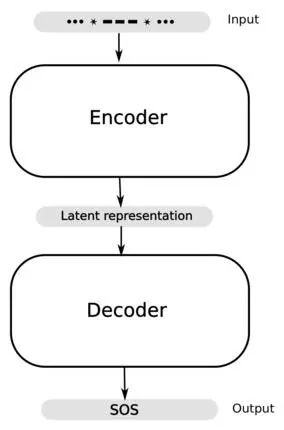
或者,我们可以构建一个 encoder-decoder 模型 来猜测(几乎)所有的单词!作为受虐狂,我们当然会选择后者。照这样说,让我们猛拍一下堂·吉诃德的战马 Rocinante,开始大战风车的征程。
AI 前线:Rocinante,西班牙语,驽骍难得 [音译],《堂·吉诃德》中堂·吉诃德所骑的马的名字。
这里有个手头问题: 我们有几个编码序列及对应的可理解的例子。使用这些例子,我们必须学习一些模式,并使用这些信息来预测新的编码标记(单词)可能会是什么。与我们预测数值结果的常见回归问题不同,我们手头有一些序列到序列(sequence-to-sequence)的学习问题,在数据中有时间结构。这是递归神经网络(RNN)可能有用的一个即时提示(它用于语音和语音数据的 RNN,以及用于图像数据的 CNN 和用于图像字母的 RNN 组合)。粗略地说,这属于一类问题:也包含了机器翻译的问题;这个模型的结构在这里起到了启发的作用。有关此主题的更多信息请参阅 [1]。限于篇幅我们不会赘述 RNN 的理论,但对于这个主题的简要介绍请参考文献 [2] 的一系列文章。
如果你想知道这个问题是否可以用不同的方法来解决,答案是:YES。马尔可夫链蒙特卡罗方法(Markov Chain Monte Carlo)会得到类似的结果。在这种情况下,我们将会遵循优秀论文 [3] 中第一个例子所提到的过程。
AI 前线:马尔可夫链蒙特卡罗算法(简写为 MCMC)的核心思想是找到某个状态空间的马尔可夫链,使得该马尔可夫链的稳定分布就是我们的目标分布 p(x)。这样我们在该状态空间进行随机游走的时候,每个状态 x 的停留时间正比于目标概率 p(x)。在用 MCMC 进行抽样的时候,我们首先引进一个容易抽样的参考分布 q(x),在每步抽样的过程中从 q(x) 里面得到一个候选样本 y,然后按照一定的原则决定是否接受该样本,该原则的确定就是要保证我们得到的原本恰好服从 p(x) 分布。
马尔可夫链,因安德烈·马尔可夫(A.A.Markov,1856-1922)得名,是指数学中具有马尔可夫性质的离散事件随机过程。该过程中,在给定当前知识或信息的情况下,过去(即当前以前的历史状态)对于预测将来(即当前以后的未来状态)是无关的。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点,每一步可以移动到任何一个相邻的点,在这里移动到每一个点的概率都是相同的(无论之前漫步路径是如何的)。
粗略地说,我们想从 (x_1,...,x_n) 输入序列预测输出序列 (y_1,...,y_m),这就涉及了条件概率(conditional probability)的学习。
AI 前线:条件概率是指事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为:P(A|B),读作“在 B 条件下 A 的概率”。条件概率可以用决策树进行计算。条件概率的谬论是假设 P(A|B) 大致等于 P(B|A)。
这里的主要障碍是,从可变尺寸的输入来预测可变尺寸的输出。在元级这一层次上,是通过将两个 RNN 组合在一起来解决的,其中,第一个 RNN 将可变尺寸的输入映射到固定尺寸的输出,另一个 RNN 接受固定尺寸输入并返回可变尺寸的输出。固定尺寸的中间向量,成为上下文矢量(context vector),它将信息从输入序列中封装起来,每次输入一个字符。产生上下文矢量的机制是使 RNN 对于捕获时间结构有用:上下文矢量是最终的 timestep 或它的某些函数之后的隐藏状态。上述条件概率使用链式法则(chain rule) 计算的。
AI 前线:链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。复合函数的导数将是构成复合这有限个函数在相应点的 导数的乘积,就像锁链一样一环套一环,故称链式法则。可见搞人工智能,学好数学非常重要。
其中,h 是上下文矢量。最后,可以使用 softmax 函数来计算上述方程右边的条件概率,该函数将字符 y_{i-1},...,y_1 的独热编码(one-hot encoded)矢量作为输入,在第二 RNN 中的递归层(recurrent layer)的输出和上下文矢量。这里使用的特定类型的 RNN 是 LSTM,有效克服了 Simple-RNN 的局限性,Simple-RNN 受到渐变问题的影响,并能够更好地捕获远程依赖关系。
AI 前线:Simple-RNN 是最简单的循环神经网络,它是 LSTM 的基础。Simple-RNN 与 BP 一样都有前馈层与反馈层。但是 Simple-RNN 引入了基于时间 (状态) 的循环机制。
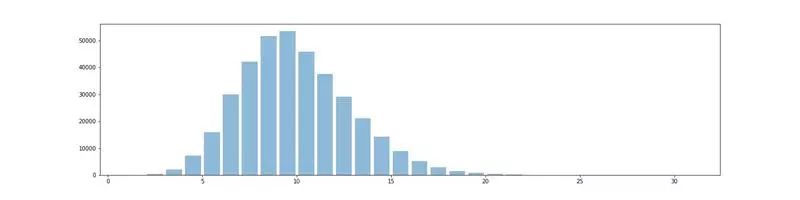
我们将引入一个特殊的字符(11)来表示每个字母的代码之间的空格。例如,SOS 的代码将表示为:...11---*...(替换...---...)。我们这样做是为了确保与给定代码相对应的单词是唯一的。接下来,我们将使用已编译数据集(words_alpha)中的英文单词,而不是用随机生成的字母集作为我们的数据。为了获得数据的感觉,参看下图所示的单词长度的直方图。从直方图上可以看出,长度超过 5 个字母的单词要比短的单词多。
对包含编码单词的数据进行训练的网络,一般会预测长的单词。请记住,网络并不会计算出生成数据的“公式”,也就是说,它并不会学习图 1 中的图表。
我们开始数据准备工作,构建一个函数,将所输入的英文单词编码为它的 Morse 电码并输出。
为了说明的目的,我们将从给定的固定长度的单词生成训练和验证数据。在这里,我们将这个长度固定为 9,因为长度为 9 的字数足够大(参见上述直方图)。注意,此举将意味着来自网络的输出单词的长度将是固定的,但是输入的 Morse 电码并不一定都是相同的长度。假定我们知道每个字母的编码长度最长是 4(其实我们不用这个特定的假设,可以选择的长度最长的 Morse 电码 max_length_x 来训练数据。)因此,如果单词的长度为 n ,那么与其对应的 Morse 电码的长度最多为 4n+(n-1),其中 n-1 对应的是 11s 的数量。我们用左边的空格填充代码,使它们的长度相同,这意味着我们输入字符的词汇表是 {‘.’, ‘—’, ‘*’, ‘ ’}。一般而言,我们让输出的字符词汇表是所有字母和空格的特殊字符。回到关于网络猜测长单词的评论,我们的意思是,由于长单词的数量会造成不平衡,因此网络将会倾向于猜测更少的空格。在下面的代码片段中,output_list 将包含英文单词,input_list 将包含填充的 Morse 电码。
现在,我们构建输入中字符的一个独热编码矢量,使输入数据适合神经网络。为此,我们构建了一个类对象(类似于 Keras 文档中的例子),它将有助于编码和解码,并将 Morse 电码和英语单词解码。我们将类分配给具有适当字符集的对象。
AI 前线:独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用 N 位状态寄存器来对 N 个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。
将数据拆分,生成一个训练集 x_train,从整个数据集 x,y 的四分之一中提取出 y_train,我们将保留剩下的四分之三作为验证集 x_val、y_val。注意,我们最好将训练集的一部分作为验证集,其余的作为测试集,但考虑我们是随便弄的设置,我们对模型构建更感兴趣,而非参数调优。现在,我们已经准备好了训练和测试(验证)数据,并且可以继续对网络进行修改。
构建神经网络的最简单方法是使用 Keras 模型和顺序 API。由于我们不需要 TensorFlow 的全部功能和灵活性,所以我们选择了 Keras。
我们所选的模型拓扑结合了简单的 RNN 的强大变体,称为长短期记忆(Long Short Term Memory,LSTM)网络。
AI 前线:长短期记忆网络是一种时间递归神经网络,适合于处理和预测时间序列中间隔和延迟相对较长的重要事件。基于长短期记忆网络的系统可以实现机器翻译、视频分析、文档摘要、语音识别、图像识别、手写识别、控制聊天机器人、合成音乐等任务。
第一个 LSTM 用作编码器,接受一个可变长度的输入序列,每次一个字符,并将其转换为固定长度的内部潜在表示。另一个 LSTM 则作为解码器,将潜在的表示作为输入,并将其输出传递到一个密集层,该层使用 softmax 函数,每次预测一个字符。
该模型的编码器和解码器组件可能具有多层 LSTM,通常并不清楚哪种拓扑最适合使用。一般来说,对机器翻译而言,深层网络工作得更好。根据经验法则,我们期望多层能够学习更高层次的时间表示,因此当数据具备了一些层次结构时,我们就会使用它。对我们来说,每层有一层就足矣。
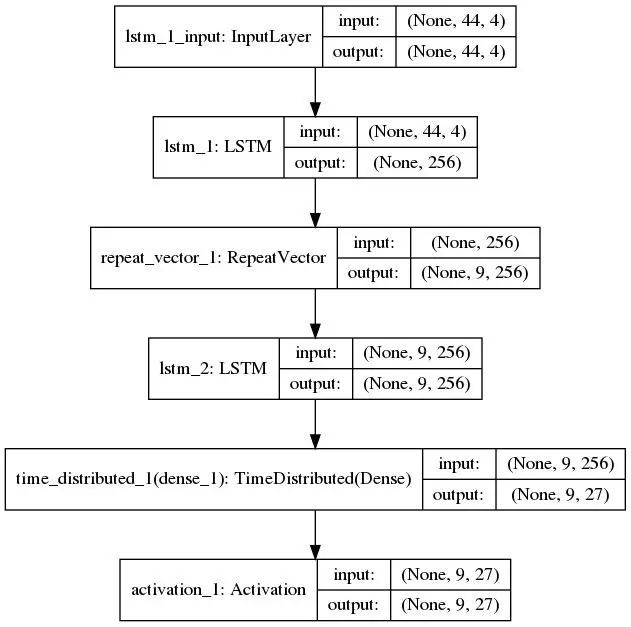
该模型使用 Sequential() 构建,并且每次只添加一个层。第一个 LSTM 层将 3D 张量作为输入,并要求用户指定输入维度。这可以用代码中指定的 input_shape 简单地完成,其中第一个组件表示时间步骤的数量,第二个组件表示特征的数量。对我们来说,特征的数量就是输入序列的词汇表中元素的数量,也就是 4,因为我们有“.”、“-”、“*”和空白字符“”。由于我们每次只提供一个独热编码矢量,因此时间步骤的数量就是 max_len_x。我们还将指定层中的内存单元(或块)的数量(此处用 latent_dim 参数表示,我们使用 256),这是潜在表示的维度。请注意,我们希望将 LSTM 的最终隐藏状态作为潜在表示返回,这包含了来自所有时间步骤的信息,即全部输入序列。如果我们使用 return_sequences = true 选项,那么将得到每个时间步骤的隐藏状态的输出,但这只包含到该步骤的序列信息。
这就得到了简单的编码器模型。我们将构建一个类似的层作为解码器。但上面的代码片段的输出是个 2D 数组。我们通过使用方便的 RepeatVector 层重复输出时间数量 max_len_y,将其转换为 3D 张量,并作为下一个 LSTM 层(解码器)。现在,我们在这个 LSTM 中使用 return_sequences = True 选项来输出隐藏状态序列,我们需要使用这些信息进行预测。为此,我们使用一个 TimeDistibuted 密集层,它输出一个长度为 max_len_y 的矢量,我们使用 softmax 激活函数来选择最有可能的字母。为了快速了解 TimeDistributed 层的目的,请参阅 Jason Brownlee 撰写的博文:How to Use the TimeDistributed Layer for Long Short-Term Memory Networks in Python。
https://machinelearningmastery.com/timedistributed-layer-for-long-short-term-memory-networks-in-python/
以下是对网络和各种输入、输出维度的快速摘要。
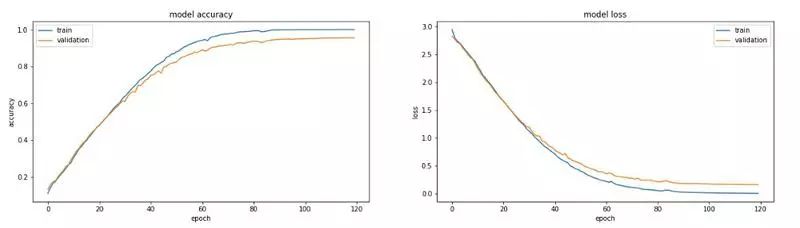
我们将模型拟合到数据中,在集合 x_train、y_train 上进行训练,并使用 x_val 和 y_val 来查看我们的工作情况。需要设置的最后一组参数是轮数(epochs)的数量和批大小。批大小是在梯度下降算法中通过网络传递的训练集的大小,然后对网络中的权重进行更新。通常批大小就是计算机内存可处理的最大值。一个轮数是通过这些批次的训练数据的全面训练一次。此处,我们设置了 1024 的批大小,使用了 120 个轮数,在下图即可看到,在大约 100 个轮数之后,精度并没有明显的增加。一般来说,看哪个参数起作用需要反复试验才知道。现在我们用 fit() 方法来拟合模型。
最后,从上面的图表可以看出,在验证集上我们可以得到大约 93% 的准确率,结果似乎并不坏。当然,如果我们增大训练数据的规模,还可以做得更好。下面是对一组随机选择的单词的预测。
在左边输入代码,中间输入相应的单词,右边输入预测。如果预测正确,那么该单词为绿色,否则为红色。
正如你所看到的,错误的预测也不算太坏。我们必须提醒自己,破译密码并没有破解代码,也就是说,弄清楚每个字母代表什么。事实上,我们可以输入字母的代码,并查看网络预测的单个字母的代码,如下所示,我们离目标还很远!
作为 encoder-decoder 模型的另一个例子,你可以尝试使用凯撒加密(Caesar cipher)或者其他代码来查看这种方法的有效性如何。
AI 前线:凯撒加密,或称恺撒加密、恺撒变换、变换加密,是一种最简单且最广为人知的加密技术。它是一种替换加密的技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例,当偏移量是 3 的时候,所有的字母 A 将被替换成 D,B 变成 E,以此类推。这个加密方法是以凯撒的名字命名的,当年凯撒曾用此方法与其将军们进行联系。凯撒密码通常被作为其他更复杂的加密方法中的一个步骤。凯撒密码还在现代的 ROT13 系统中被应用。但是和所有的利用字母表进行替换的加密技术一样,凯撒密码非常容易被破解,而且在实际应用中也无法保证通信安全。
References:
[1] Sequence to Sequence Learningwith Neural Networks
http://papers.nips.cc/paper/5346-sequence-to-sequence-learning-with-neural-networks.pdf
[2] Understanding LSTM Networks
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
[3] THE MARKOV CHAIN MONTE CARLO REVOLUTION
http://www.ams.org/journals/bull/2009-46-02/S0273-0979-08-01238-X/S0273-0979-08-01238-X.pdf
想看更多这类文章, 请给我们点个赞吧!