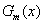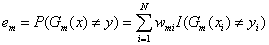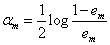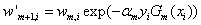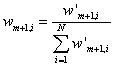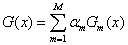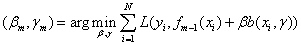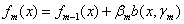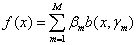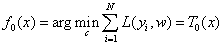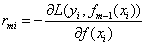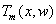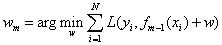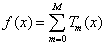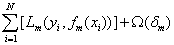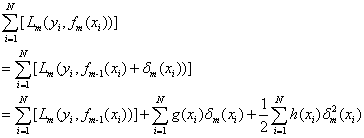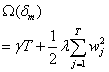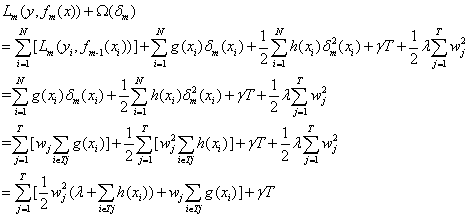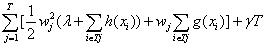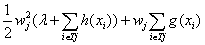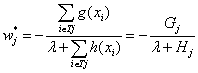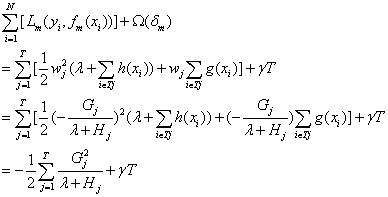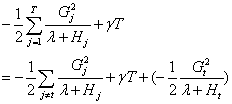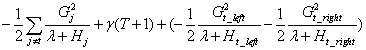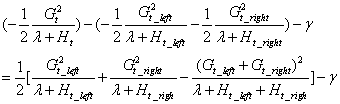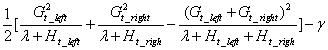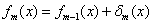会员服务 ·

Boosting硬核入门-XGBoost

2019 年 10 月 30 日 AINLP

1 Boosting方法概述

本文需要读者有以下的前置知识储备：决策树算法、梯度下降法、泰勒展开式。

1.1 集成方法

集成方法（Ensemble Learning）是一种应用得非常广泛的机器学习方法，主流的集成方法包括Bagging、Boosting、Stacking。

俗话说“三个臭皮匠，顶个诸葛亮”，这就是集成方法的思路。很多时候，我们无法直接训练出优质的模型（强学习机），而只能得到一些较差的模型（弱学习机）。集成方法就是将多个弱学习机的预测结果综合起来，以达到甚至是超过强学习机的预测效果。

Bagging采用并行组合弱学习机的思路，代表算法是随机森林（RF，RandomForest），Bagging在降低方差方面有很好的效果。

Boosting采用串行组合弱学习机的思路，代表算法是XGBoost和LightGBM，Boosting在降低偏差方面有很好的效果。

本文将要介绍的是Boosting。

1.2 Boosting方法

Boosting是一种串行的集成方法，每轮迭代后算法会计算当前模型预测值和样本实际值的差异度，下一轮迭代会针对这个差异度来继续训练模型。这个差异度有时也叫残差，它可以是平方损失函数、指数损失函数（AdaBoost）、对数损失函数（逻辑回归）、Hinge损失函数（SVM），等等。

AdaBoost算法是早期的经典Boosting算法，它是前向分布算法的一个特例。AdaBoost采用指数损失函数来评估差异度，指数损失函数的缺点是对于异常点非常敏感，因而在噪音比较多的数据集上经常表现不佳。

GBDT算法在健壮性方面做了改进：它结合了CART决策树和梯度提升方法，由于CART树是复杂度低的树，所以方差很小，能够很好地解决过拟合的问题；同时GBDT可以使用任何损失函数 (只要损失函数是一阶连续可导的)，这样一些比较健壮的损失函数就能得以应用，使模型抗噪音能力得到增强。

XGBoost和LightGBM是现在最流行的Boosting算法，它们被广泛用于kaggle、天池等竞赛中。Boosting共有的缺点是模型串行训练，难以并行处理，这样在数据量增大时，无法通过大数据技术提高训练速度，而xgb和lgb在这方面做出了突破，极大地提高了训练速度，这在后文中会详细说明。

2 AdaBoost算法和GBDT算法

第2节将会简要地介绍AdaBoost算法和GBDT算法，偏重于应用而非理论的读者，可以跳过本节。

2.1 AdaBoost算法概述

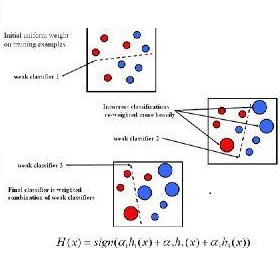
如前文所述，AdaBoost是一个串行算法，通过M轮迭代，在每轮迭代中都训练出1个分类器（分类器可以根据需要，采用任意合适的模型），最后将这M个分类器相加，得到最终的预测模型。

在构建模型的过程中，我们需要对被错误预测的样本赋予更多的关注，让这些样本在下一轮迭代过程中能够更大地影响分类器模型的构建，所以我们要提高被错误预测的样本的权重。

在最后组合模型的过程中，我们需要让预测效果更好的模型，起到更大的作用，以提高最终模型的预测效果，所以我们要提高预测效果好的分类器的权重。

以上两点，就是AdaBoost在构建模型的过程中，需要遵循的思路。

2.2 AdaBoost算法流程

我们利用AdaBoost算法，对一个包含有N个样本的数据集，进行M轮迭代，构建预测模型。

其中，表达式的下标m表示迭代的次数，下标i表示样本标号。

算法流程如下：

（1）初始化样本权重，将每个样本的权重w设置为1/N。

（2）进行M次循环迭代，依次求得M个分类器

（2.1）通过计算，获取此次迭代的最优分类器（根据实际需要，采用合适的分类模型）:

（2.2）计算此次迭代分类器的误差：

（2.3）计算此次迭代分类器的权重：

如此设置分类器权重的思路是：在构建最终模型时，要对M个分类器加权相加，为了得到更好的分类效果，就要赋予误差低的分类器高权重，赋予误差高的分类器低权重。

（2.4）更新样本的权重：

如此设置样本权重的思路是：为了能够让被错误分类的样本，在下一轮迭代中对分类器的构建产生更大的影响，从而达到纠正错误的目的，就需要赋予被错误分类的样本高权重，赋予被正确分类的样本低权重。

最后对样本权重进行归一化：

归一化的目的是：保证所有样本的权重和为1。

（3）最后，将所有分类器加权求和，获得最终分类器：

2.3 前向分布算法流程

前向分布算法比AdaBoost算法更为简洁，我们可以通过学习前向分布算法，进一步了解Boosting算法的思路。

另外，可以证明，AdaBoost算法是前向分布算法的一个特例（证明过程见李航《统计学习方法》8.3.2）。

前向分布算法流程如下，其中表达式的下标m表示迭代的次数（一共迭代M次），下标i表示样本标号（一共有N个样本）：

（0）记损失函数为：

并初始化：

（1）进行M次循环迭代，依次求得M个分类器（求得分类器的参数和权重）

（1.1）求解最优化问题，通过极小化损失函数，求得β和γ：

（1.2）根据求得的β和γ，更新f(x)：

（2）整理得到最终模型：

2.4 GBDT算法概述

AdaBoost算法使用指数损失函数作为损失函数，所以求解最优化问题的过程较为简单，与之类似还有平方损失函数。但是，如果采用其它损失函数，求解最优化问题就有可能较为困难。

为了解决这个问题，同时也为了能够采用一些更健壮的损失函数以减小异常点的影响，我们采用损失函数的梯度作为残差。我们可以采用任意损失函数，只要这个损失函数一阶可导。

由于CART树模型较为简单，GBDT算法利用CART树作为基本学习机，这样能够弥补Boosting算法方差较高的缺点。

2.5 GBDT算法流程

我们要利用GBDT算法，对一个包含有N个样本的数据集，进行M轮迭代，构建预测模型。

其中，表达式的下标m表示迭代的次数，下标i表示样本标号。

算法流程如下：

（1）初始化f(x),并记为T0(x)：

（2）进行M次循环迭代，依次求得M个决策树。

（2.1）遍历所有样本，对每个样本的损失函数求导，记为样本的残差：

（2.2）将所有样本的值，替换成残差。

（2.3）以所有样本的新值（残差）为训练样本，训练并输出决策树模型：

其中，每个叶子节点输出的值w为

在这里，w不是一个常数，在不同的叶子节点区域，w取不同的常数值。

在这一步中，需要求得决策树模型两方面的内容，一是决策树的结构（使用哪些特征进行分割，分割点的值是多少），二是叶子节点的输出值。

（2.4）根据T(x,w)，更新f(x)

（3）最后，整理输出最终的GBDT模型

3 XGBoost算法

3.1 概述

Boosting算法最大的缺点有两个：一是方差过高，容易过拟合；二是模型的构建过程是串行的，难以应用于大数据场景。这两个问题在XGB算法中，都得到了很大的改善。

过拟合的问题还算好解决，很多类似的研究结论都可以被拿来借鉴。所以，在我看来，XGB最大的贡献，就是创造性地给出了Boosting算法的并行计算思路，使之能够适应大数据场景，应用于大数据分布式集群环境中。

下面，我们将先学习XGB算法，然后对它的特性进行归纳总结。

3.2 目标函数

要构建一个模型，我们首先要确定要以什么目标来衡量模型的好坏，然后再围绕这个目标，一步步地改进模型。所以，在XGB算法中，我们要先确定算法的目标函数。随后，XGB模型的构建，就是以实现这个目标函数最小化为目标。

XGBoost的目标函数包括损失函数和正则项两个部分。

损失函数衡量的是模型输出值和样本真实值的差异度，差异度的值越低，模型越好。

正则项衡量的是模型的复杂度，复杂度越高，模型越容易过拟合，所以正则项的值越低，模型越好。

如下式所示，第一项L(y,y’)表示的是模型的损失函数，第二项Ω(δ)表示的是模型的正则项。

其中f(x)表示前m次迭代生成模型之和，δ(x)表示当前迭代轮次生成的模型，表达式的下标m表示迭代的次数（一共迭代M次），下标i表示样本标号（一共有N个样本），下标j表示叶子节点标号（一共有T个叶子结点）：

将损失函数进行泰勒展开，并且记g(x)为L(y,y’)的一阶导数，h(x)为L(y,y’)的二阶导数：

（注：g(x)和h(x)均为损失函数L(y,y’)对变量y’的求导，此时y为常数）

正则项表示如下，其中T表示叶子节点的个数，w表示叶子节点的输出值

注：本文中使用的是L2范数。在XGB的实际应用中，可以使用L1范数。

最后，代入以上损失函数和正则项的表达式（第2行），删除常数项（第3行），最后按叶子节点汇总（第4、5行），可得：

其中Tj表示属于不同叶子节点（模型输出的预测值，而非真实值）的样本的集合。i∈Tj表示经过当前迭代轮次模型的预测，第i个样本被分到叶子节点j处。

确定了目标函数，下一步就是构建决策树模型。决策树模型的构建包括两个方面：一是要确定决策树模型的结构，包括每个节点使用什么特征进行分割，分割点的值是多少；二是要确定每个叶子节点的输出值。

接下来的两个小节，将分别通过计算叶子节点的输出值和进行节点分裂判定，来完成对决策树模型的构建。

3.3 计算叶子节点输出值

我们先假设决策树的结构已经被确定了，那么在这个前提条件下，我们尝试计算叶子节点的最优输出值。

观察目标函数：

最后一项γT只与决策树的结构有关，在结构确定的情况下是常数，可以忽略。

第一大项可以按叶子节点j进行分解，分解后的子项互不相关。所以可以根据以下表达式，按叶子节点j进行划分，各自单独求解w的最优值：

显而易见的，这是一个一元二次多项式，w的最优解为：

其中，为便于书写和记忆，记：

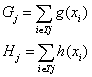
3.4 节点分裂判定

在求得叶子节点的最优输出值后，我们接下来求解决策树的结构。

由于树的组成结构有无穷多种，我们无法穷举遍历所有的情况，所以我们采用贪婪算法，在每个节点都进行一次判定，决定是否该分裂这个节点，以及该如何分裂这个节点，以此逐步迭代构成一棵决策树。

我们先将上一节求得的w的最优解代入目标函数，可以得到目标函数的表达式：

当我们判定一个叶子节点是否需要分裂时，需要计算分裂操作执行前后，目标函数的变化情况。记待分裂节点为t。

分裂前整棵树的代价函数：

分裂后整棵树的代价函数：

将以上两式相减，可得：

这个式子即为是否分裂节点的判别公式。如果该式大于0，则表示目标函数的值减少了，分裂是有增益效果的，可以分裂。如果该式小于0，则表示分裂后的目标函数反而增加了，则不建议分裂。

注：

在单机版的XGB算法中，使用的是精准贪婪节点分裂算法。算法会遍历所有特征的所有值，以判定：是否分裂、如果分裂的话采用哪个特征进行分裂、分裂点选取为什么数值。

在数据无法全部放到内存中的场合，或者在分布式应用的场合，XGB使用近似节点分裂算法。XGB首先根据样本数据的百分位分布计算出备选分割点，然后将连续的样本数据分配到由这些备选分割点确定的桶（bucket）里，最后汇总数据（不同分布式集群上的数据、或不同处理线程上的数据），并求出最优分割点。

3.5 XGBoost算法流程

在这一小节，我对前面几个小节得出的结论进行整理，归纳出XGBoost的算法流程。

其中，f(x)表示前m次迭代生成模型之和，δ(x)表示当前迭代轮次生成的模型，表达式的下标m表示迭代的次数（一共迭代M次），下标i表示样本标号（一共有N个样本），下标j表示叶子节点标号（一共有T个叶子节点）：

（1）根据实际场景需求，设计损失函数L(y,y’)和正则项Ω(δ)。进行f0(x)的初始化。

（2）进行M次循环迭代，依次求得M个决策树。

（2.1）在每次迭代开始前，遍历所有样本，计算所有样本的损失函数L(y,y’)关于y’的一阶导数g和二阶导数h。

（2.2）使用以下表达式，进行节点分裂判定。逐步迭代生成树，以确定决策树结构：

表达式大于0则可以分裂，小于0则不建议分裂。

（2.3）决策树结构确定后，根据下式，计算当前迭代轮次决策树的叶子节点输出值：

（2.4）根据当前迭代轮次生成的决策树δ(x)，更新模型f(x)：

（3）整理输出最终的XGBoost模型：

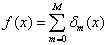
在接下来的几个小节里，我将会对XGB的特性进行归纳总结，包括前文提及的过拟合预防方法、大数据场景实现方法、以及其它的一些特性。

3.6 大数据场景实现方法

（1）样本间并行计算：在每次迭代前，需要遍历所有样本，求解损失函数的一次导数g和二次导数h，由于不同样本间无相关性，故此时可以对不同的样本使用并行计算。

（2）特征间并行计算：在进行节点分裂判定时，需要遍历所有特征，此时可以对不同的特征使用并行计算，最后再汇总不同特征的判定结果，输出最优解。

（3）预排序：在每次迭代前，事先将样本数据按照不同的特征，根据其数值进行预排序，方便后续在节点分裂判定环节，顺序访问样本数据，对一阶导数和二阶导数进行取数和累加。（注：在构建树的过程中，耗时最长的步骤，就是对样本数据进行排序）

（4）块压缩技术(Block Compression)：按列（特征）对数据进行压缩，在数据被读取入内存时，通过一个额外的线程进行解压。这个技术是将磁盘读写的时间耗费，转嫁到内存解压缩的时间耗费上。

（5）块共享技术(Block Sharding)：将数据存储到不同的磁盘上，通过额外的线程预读取数据，将数据提前读取到不同磁盘各自的内存缓冲区里，在需要的时候，再将数据送到模型训练线程中。这个技术减小了磁盘读写的时间耗费。

（6）数据预读取：建立一个独立的线程，在模型执行运算操作的同时，用这个线程向磁盘读取后续需要用到的数据。但是，由于程序在计算模型时常常也要读写磁盘，所以这个方法未必很有效。

（7）构建树的算法包括精确贪婪算法和近似算法（直方图算法），近似算法对每维特征按照分位数进行分桶(bucket)。

3.7 过拟合预防方法

（1）学习效率参数shrinkage：类似于其它算法的学习效率参数LearningRate。

（2）引入正则项：包括树的叶子节点数量，叶子节点输出值的L1或L2范数。

（3）列（特征）采样：在迭代时只使用一部分特征来构建模型。列采样不仅缩短了计算时间，还提高了模型的预测效果。列采样方法源自于随机森林算法。

（4）行（样本）采样：在迭代时只使用一部分样本来构建模型。

3.8 其它特性

（1）自定义目标函数：XGB可以自定义目标函数，只需要目标函数满足二次可导。

（2）基分类器：不仅可以采用CART树作为基分类器（本文中默认使用CART树），也可以使用线性模型。

（3）分裂准则：节点分裂时，能够直接根据目标函数（损失函数+正则项）进行判定。

（4）有效处理缺失值和稀疏值：对于特征值缺失或特征值稀疏的样本，分别尝试将缺失\稀疏数据划分到左叶子和右叶子，计算增益并进行对比，选择增益更大的划分方案。

（注：产生稀疏矩阵的三个常见原因：数据缺失，数据本身含有大量零值，使用了one-hot方法。）

（5）XGBoost允许在每一轮boosting迭代中使用交叉验证。因此，可以方便地获得最优boosting迭代次数。而GBDT只能使用网格搜索（Grid Search）检测有限个值。

（6）支持加权数据：陈天奇在论文里提了一下，但是没给出具体算法。

参考资料

[1] Tianqi Chen AScalable Tree Boosting System

[2] Tianqi Chen Introductionto Boosted Trees

[3] 李航统计学习方法清华大学出版社

本文转载自公众号：数论遗珠，作者：阮智昊

推荐阅读

支持向量机(SVM)硬核入门-基础篇

神经网络硬核入门-反向传播(BP)算法

NLP硬核入门-Seq2Seq和Attention机制

NLP硬核入门-隐马尔科夫模型HMM

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLP君微信(id：AINLP2)，备注工作/研究方向+加群目的。